Mengenlehre – die neusten Beiträge

Könnte das jemand "normal" für Anfänger erklären, war bei paar Foren und da wurde z. B. gesagt, dass Sprachen Teilmengen des karthesischen Produkts sein. Dann war meine Frage, aber Relationen sind ja auch Teilmengen des karthesischen Produkts, dann hieß es, ja aber sind nicht das gleiche. Was ist dann der Unterschied von einer Sprache und einer Relation? Tupel von karthesischen Produkten sind die Wörter oder? Wenn ja was ist dann das Alphabet?

Was genau soll M* darstellen, dass es eine Sprache ist?

Hallo, kann man dies mit logischen Äquivalenzen beweisen/zeigen?

Danke.

Hallo, ich sollte beantworten und begründen, ob folgende Aussage wahr oder falsch ist.

”Es existiert genau eine Primzahl mit folgender Eigenschaft: p + 2 ist prim und p + 4 ist prim.”

Für mich gäbe es nur eine, p = 3.

Also wahr.

Jedoch kann man ja über die Verteilung der Primzahlen generell nichts sagen.

Könnte diese Aussage also falsch sein?

Aufgabe:

Meine Überlegungen:

a) Es gibt 6 Relationen.

(1,x) (1,y), (1,z), (2,x), (2,y), (2,z) → richtig?

b) Ich weiß nicht wie man das schreibt.

die Zweite Zahl in der Klammer ist immer das Ergebnis, von der 1. Zahl multipliziert mit dem unterschied der vorherigen zahl

also 1*1 = 1

2*4 = 8 (4-1=3)

3*9 = 27 (9-4=5)

4*16=64 (16-9=7)

5*25=125 (25-16=9)

also die different zwischen dem zweiten Faktor und dem Vorgänger ist immer eine ungerade zahl, aber ich weiß nicht wie man das schreibt

weiter würde es ja gehen mit 6*36=396 (36-25=11)

c) handelt es sich um eine Abbildung? → weil jeder Urbildmenge wird ein Urbild zugewiesen wird oder?

wäre nett wenn ihr mir bei den aufgaben a,b,c feedback geben könntet und vor allem wie ich bei b) diese zuordnungsvorschrift formuliere?

Folgende Aufgabe:

Meine Überlegungen:

a) Muss ich hier die Zahlen von 1-8 nehmen (M₈) und dann die Zahlen von 1-6 (M₆) und dann schaue ich für welche Zahlen aus der Menge M8 durch die Zahlen der Menge M6 ein k aus den natürlichen Zahlen entsteht?

Also 1:1 = 1; 2:1=2 ; 2:2 = 1, 3:1 = 3, 3:3 = 1; 4:1 = 2 ; 4:2 = 2 ; 4:4 = 1; 5:1 = 5 ; 5:5 = 1; 6:1 = 6 ; 6:2 = 3 ; 6:3 = 2 ; 6:6 = 1,

7:1 = 7; 8:1 = 8, 8:2 = 4; 8:4 = 2

Und diese müsste ich mit Pfeilen darstellen oder? Also von der 8 bspw. geht ein Pfeil zur 1,2 und 4. Habe ich das richtig verstanden?

b) reflexiv, weil x in Relation zu y steht

transitiv → die Begründung verstehe ich nicht :( bitte helfen!

es ist nicht symmetrisch, da ich die Reihenfolge nicht ändern kann. Hinsichtlich der vorgegebene Relation ist (6,1) nicht dasselbe wie (1,6) oder?

Ich habe Probleme mit (b), (c) und (e).

Wie ist dies zu interpretieren? Was bedeutet hier g(x), f(x)? (e) ist nicht mal eine Relation, bzw. schlecht definiert, wenn man mich fragt.

kann mir jmd helfen? Danke ☺️

Guten Abend meine Mathefreunde.

Die Aufgabe lautet: https://gyazo.com/d004ace453e3ceb3dccc3a09f446118e

1. Mein Ansatz war: Schnittmengen der M aufzulösen und daraus eine vereinigungsmenge zubasteln, aber irgendwie weiß ich nicht, wie ich genau anfangen soll.

2. Ansatz wäre: Für alle i existiert ein I : x existiert aus Mi

              es gibt ein i dafür existiert I : x existiert nicht aus Mi

      danach beide fälle kombinieren, aber ich bin mir nicht sicher

Hallo ich habe folgende Aufgabe: bilden Sie eine Obermenge M aus den Zahlen 1-20; bilden Sie Teilmengen A,B und c

teilmengen habe ich bestimmt (A=gerade Zahlen, B=Primzahlen, C=alle zweistelligen Zahlen), Schnittmengen AnB, AnC, BnC sind auch schon bestimmt.

aber wie bilde ich jetzt die Obermenge, ist das nicht einfach wie die Schnittmenge?

(x ∈ X ∧ x ∈ Y) ∨ x ∈ Z ⇔ x ∈ X ∨ (x ∈ Y ∧ x ∈ Z)

Kann ich das Distributivgesetz anwenden und schreiben:

(x ∈ Z ∨ x ∈ X) ∧ (x ∈ Z ∨ x ∈ Y) ⇔ (x ∈ X ∨ x ∈ Y) ∧ (x ∈ X ∨ x ∈ Z)

⇔

(x ∈ Z ∨ x ∈ Y) ⇔ (x ∈ X ∨ x ∈ Y)

Dann sieht man ja dass es auf der einen Seite wahr ist wenn x ∈ Z, und auf der anderen Seite falsch ist. Also können die Aussagen nicht äquivalent sein. Kann man das so beweisen?

Aufgabe b) :

Meine Antwort:

Das rote ist vom Lehrer

Ich weiß nicht was ich falsch gemacht habe kann mir wer helfen?

Nehmen wir an, wir haben eine Menge A, welche aus einer beliebigen Anzahl Tupeln mit jeweils einer beliebigen Anzahl an Komponenten besteht. Die Komponenten können jedoch zwischen den einzelnen Tupeln durchaus gleich sein. Wie kann man aus dieser Menge nun formell eine Menge B bauen, in welcher nur Tupel mit einzigartigen Elementen vorhanden sind?

Zur Veranschaulichung, nehmen wir an, wir haben die folgende Menge A:

 Das dritte Tupel hat genauso wie das zweite Tupel die 4 als Komponente. Wie kann man allgemein, zum Beispiel in intensionaler Schreibweise, daraus die Menge B bauen, sodass in diesem Beispiel

oder auch (ist für den eigentlichen Anwendungszweck egal):

 ?

Ich hoffe, es ist verständlich, worauf ich hinaus will. Ich hab versucht, mir da in intensionaler Schreibweise irgendwas zu reimen, hab aber einen Knoten im Kopf. Ich hatte irgendwas stehen mit:

aber das sieht mir irgendwie nicht richtig aus. Ich will quasi ausdrücken "Nehme jedes Element ai aus A, wobei xj Element/Komponente in ai ist und xj nicht in ai-1, ai-2, ..., ai-n vorhanden ist.

Suche einen Beweis für den obenstehenden Satz. x ist Element der ganzen Zahlen und n Element der positiven Natürlichen Zahlen. Ich habe es mit der Kontraposition versucht, komme aber leider nicht weiter. Mein Ansatz war folgender:

A= x ist ungerade

B= x^n ist ungerade

A->B = nichtB -> nichtA (Kontraposition)

nun muss also bewiesen werden dass wenn x^n gerade ist x auch gerade ist

eine gerade zahl ist ein vielfaches von 2 daher gilt:

x^n =2k

dann müsste

x= n-te Wurzel von 2k sein

ab hier komme ich jedoch nicht weiter...

Hallo, weiß jemand wie man die Mächtigkeit einer Menge bei Wolfram alpha eingeben kann?

Hallo liebe Community,

ich rechne gerade eine Aufgabe die wie folgt lautet:



Was ist ?

Ansich hatte ich das Gefühl Urbilder ganz gut zu verstehen.

Wenn man f(x)=x^2+1 hat und f^-1(3) bestimmen soll, dann setze ich einfach die 3 für y in meiner Funktion ein und bestimme das entsprechende x dazu.

So bei Funktion f wollte ich nun wie folgt vorgehen:

Ich setze erst 0 für y ein und dann 1 für y. Aber jetzt war ich schon etwas verwirrt, weil es eine Funktion mit 2 Variablen ist x und y. Meine erste Idee war erst jedes y durch 0 zu ersetzen also so: 0 = x*0-0^2

Das hat aber für mich keinen Sinn mehr gegeben, weil das ist dann ja für jeden Wert von x wahr und wie soll ich das als Ergebnis aufschreiben.

Dann habe ich es noch wie folgt ausprobiert: 0 = x*y-y^2

Und kam dabei auf folgende Lösung x=y oder y=0.

Dann habe ich so weitergerechnet: 1=x*y-y^2 und kam auf folgendes Ergebnis: y+1/y

Mein Ergebnis für das Urbild f^-1([0,1]) ist dann folgendes: {y,0,y+1/y}. Ist das so korrekt?

Nun habe ich weitergerechnet mit g. Da soll ich für y das kartesische Produkt von 5 und den Reelen Zahlen einsetzen. So hier war ich eigentlich schon geliefert. Wenn man das kartesische Produkt von 5 x R bildet hat man ja Paare, aber eine unendliche Anzahl von Paaren und ich kann ja schlecht unendlich viele Paare für y einsetzen, da werde ich ja wortwörtlich nie fertig mit.

Dann habe ich mir gedacht okay, y muss das Paar (3x,7) sein. Damit also die Gleichung wahr ist muss man die Relle Zahl 7 nehmen dann hat man für y das Paar (5,7) also gilt (5,7)=(3x,7) und dann muss ich nur noch die Gleichung hier lösen: 5 = 3x also x = 5/3. Und dann ist die Lösung für das Urbild von g^-1(5xR)={5/3}???

Kann mir bitte jemand erklären ob ich das richtig gerechnet habe bzw. gedacht habe oder falls ich halt einen Fehler gemacht habe mir erklären wo mein Fehler liegt.

Das wäre wirklich sehr nett von euch :)

Also ich (16) mache ein Juniorstudium und bin ein wenig mit einer der Übungsaufgaben überfordert. Mir würde vorerst eine Lösung reichen, da wir das bis morgen abgeben müssen und mir das auch jemand anderes erklären kann, allerdings nicht mehr heute. Die Basics habe ich alle schon verstanden.

Die Aufgabe lautet wie folgt:

Danke schon mal im Vorraus :)

Hallo liebe Community,

ich beschäftige mich immer noch mit dem Thema Aussagenlogik und will erneut eine Verständnisfrage stellen. Ich probiere gerade den indirekten Beweis oder auch Beweis durch Widerspruch zu verstehen.

Meinem Verständnis nach funktioniert der Widerspruchsbeweis wie folgt:

Man nimmt eine Aussage S und negiert diese. Der Widerspruchsbeweis funktioniert nur wenn die negierte Aussage S den Wahrheitswert falsch hat. Wenn die negierte Aussage von S den Wahrheitswert falsch hat, dann kann man die negierte Aussage S nocheinmal negieren.



Dadurch, dass die doppelt negierte Aussage von S eindeutig wahr ist, und die doppelte Negation von S wieder S ergibt hat man dadurch bewiesen, dass S wahr ist.

Ansich habe ich das Gefühl, dass ich es teilweise verstanden habe, aber ich habe es noch nicht in der Gänze verstanden.

Ich möchte die ganze Zeit den Beweis durch Widerspruch als logische Formel aufstellen und dann wollte ich probieren diese logische Formel, formal zu beweisen. Mit vielleicht einer Wahrheitswertetabelle.

Das habe ich auch schon irgendwie ein bisschen ausprobiert und hatte folgendes:

Nur irgendwie habe ich diese Wahrheitswertetabelle erstellt ohne mir im klaren zu sein, was ich da so wirklich mache. Ich habe meiner Meinung nach immer noch keine logische Formel für den Beweis durch Widerspruch.

1. Was ist die logische Formel des Beweises durch Widerspruch.
2. Ergibt meine Wahrheitswertetabelle Sinn im Bezug auf den Beweis durch Widerspruch?
3. Wenn meine Wahrheitswertetabelle Sinn ergibt, kann mir jemand kurz zusammenfassen warum diese Wahrheitswertetabelle Sinn ergibt?

Anmerkung zu der letzten Frage: Ich bin halt ein bisschen verwirrt im allgemeinen, da ich nicht weiß wie ich damit umgehen soll falls die Aussage S falsch ist. Weil dann funktioniert ja der Beweis durch Widerspruch eigentlich nicht, weil ich dann die Negation von S nicht zu einem Widerspruch bringen kann, oder?

Kann mir jemand hierbei helfen, weil hier Variablen gegeben sind und keine Zahlen. Weiß nicht wie ich da vorgehen soll 😕

Hi!

Ich habe eine Frage zu einer Stochastikaufgabe.

Ein Würfel wird n-mal geworfen. A ist das Ereignis, dass keine 6 geworfen wird und B das, dass keine 5 geworfen wird.

Ich soll nun die Wahrscheinlichkeiten mithilfe der Formel von Poincare-Sylvester berechnen. Es geht um die Wahrscheinlichkeiten

• 
• 
• 
• 

Danke im Voraus!

1. Prüfen Sie jeweils mit Hilfe von Venn-Diagrammen die allgemeine Gültigkeit der folgenden Aussagen:

folgendes Bsp. : (𝐴∪𝐵)∩𝐶=(𝐴∩𝐶)∪(𝐵∩𝐶)

Kann mir das vielleicht jemand erklären? Ich Blick da gar nicht durch...

Wie zeige ich die Werte der Differenzmenge in einer Wahrheitstabelle an? 

Angenommen, A ist 0 und B ist auch 0. Bedeutet das, dass der Wert x weder in A noch in B enthalten ist? Ist der Wert von A\B dann 0?

Mir fiel beim Durchlesen ( https://de.m.wikipedia.org/wiki/Klassenlogik ) auf, dass es eine sog. Klassenlogik gibt, die etwas an die Syllogistik des Aristoteles erinnert. Allerdings fällt dann schnell auf, dass die Prädikatenlogik ja im Prinzip dasselbe ist (eben nur modernisiert). Mir erschließt sich nicht ganz, was hier nun der Unterschied zwischen Prädikatenlogik und Klassenlogik ist.

Auch das Zitat von Oberschelp ist hierbei interessant, indem er sagt, dass eine klassenlogische Sprache der tatsächlich verwendeten Mathematik mehr entspräche als die prädikatenlogische Sprache. Wie genau ist das gemeint? Kennt sich damit jemand genauer aus?

Hallo,

Mein Prof meinte, dass man das Morgansche Gesetz mit der Logik begründen kann.

Ich denke er meint, dass man die Negation einer Aussage mit dem Komplement gleichsetzen und dann mit den Verknüpfungen arbeitet. Aber warum ist das Konplement gleich der Negation?

Danke

Es ist schwer eine Mengengleichheit zu beweisen oder widerlegen?

Hallo,

hätte eine Frage zur Schnittmenge und Teilmenge. Könnte man im Prinzip sagen, das es das gleiche ist, da

A:(1,2) B:(1,2,3,4,5,6)

A⊂B und A∩B?

Guten Tag,

angenommen man hat folgende Mengen:

• X = {(1,a), (2,b)}
• Y = {(3,c), (4,d)}

Nun soll das karthesische Produkt X x Y gebildet werden; ist die richtige Antwort 1. oder 2. ?

1. X x Y = {((1,a),(3,c)), ((1,a),(4,d)), ((2,b),(3,c)), ((2,b),(4,d))}
2. X x Y = {(1,a,3,c), (1,a,4,d), (2,b,3,c), (2,b,4,d)}

Vielen Dank für alle Antworten :)

Moin Leute,

Und zwar brauche ich Hilfe bei diesen Aufgaben. Also bzw. Bei der 2 eher. Die Aufgabe 1 und 3 habe ich einigermaßen noch geschafft, aber bei der 2 war ich verloren. Kann mir da jemand bitte helfen! Wenn ihr Anmerkungen oder Ergänzungen zur Aufgabe 1. und 3. hättet, wäre es nett. Danke!

Angenommen ich zeichne mit einem Stift auf einem Blatt Papier eine Linie und setze irgendwann zufällig ab. Wenn man jetzt die Länge dieser Linie in cm angibt, wie hoch ist die Wahrscheinlichkeit, dass diese cm-Anzahl eine rationale bzw. irrationale Zahl ist? Ich weiß, dass die Menge der irrationalen Zahlen eine höhere Kardinalität besitzt, als die Menge der rationalen Zahlen und es daher ja mehr irrationale Zahlen gibt als rationale Zahlen. Dennoch finde ich keine Antwort auf dieses Problem.

Ich hoffe, mir kann jemand helfen!

A.

Die Menge M_1 wird aus den einzelnen chemischen Reaktionen, bei denen Wasserstoff abgegeben wird, gebildet.

Die Menge M_2 besteht aus den chemischen Reaktionen, bei denen in einem Kohlenwasserstoff ein H-Atom durch ein Cl-Atom ersetzt wird.

Gib einige Beispiele für die Elemente dieser Mengen an. Sind die beiden Mengen gleichmächtig?

Meine Frage zur Lösung (im Bild) wäre: Wie kommt man darauf, dass M_1 mächtiger als M_2 ist?

Hallo zusammen, ich bin momentan in einer Ausbildung. Und es wird immer mehr mit diesen komischen Menge von usw. gerechnet bzw eher definiert und ich habe überhaupt kein Plan was ich damit anfangen soll, weil mir wurde es nie beigebracht. Habe auch nur Realschule aber in Mathe und Physik eine 1.

Soll ich mir das einfach selber beibringen und wenn ja, hat jemand eine gute Quelle?

Hallo,

Könnte mir jemand ein Beispiel für dort unten für diese formale Darstellung geben? Ich verstehe die Zeichen, aber kann mir daraus kein alltägliches Beispiel rekonstruieren oder irgend ein banales Beispiel.
Ist dieses a jetzt eine Eigenschaft oder habe ich da was falsch verstanden?

Was kann ich mir unter der Menge Ia:I vorstellen? Was bedeutet das a in diesem Zusammenhang und was bedeutet der Doppelpunkt?

Ich konnte die Frage selbst beantworten. Es handelt sich nicht um eine Menge. Ia ist einfach der Name der Funktion. Tut mir Leid, es ist noch früh.

Hallo,

da ich oft verschiedene Versionen sehe, wollte ich euch heute mal fragen, wie ihr das doppelgestrichene N schreibt:

?

Guten Morgen (um halb 2),

Bei dieser Aufgabe scheiden sich momentan leider die Geister, was die Lösung angeht.

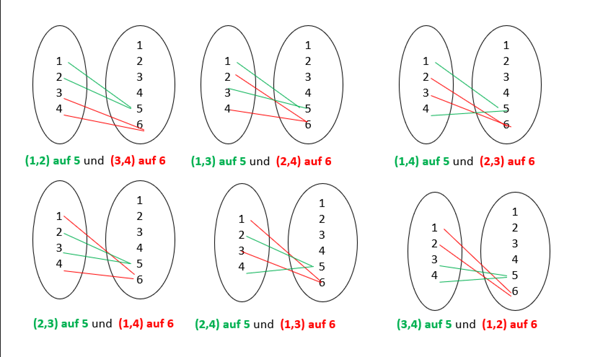
Wieviele Abbildungen von {1,2,3,4} nach {1,2,3,4,5,6} gibt es, für die die Bildmenge(i) zwei Elemente hat

Die offizielle Musterlösung behauptet folgendes

"Bei diesem Fall müssen wir besonders aufpassen, denn hier gibt es 2 Fälle. Erstens: 3 Zahlenwerden auf eine Zahl abgebildet und eine Zahl auf eine Andere. Zweitens: Jeweils 2 Zahlen bilden auf die selbe Zahl ab.Bei beiden Fällen gibt es 2 Zahlen im Bildbereich, die beliebig aber unterschiedlich gewähltwerden dürfen. Daraus folgen schon mal 6·5 M öglichkeiten. Im ersten Fall müssen 3 der 4 Argumente auf die selbe Zahl abgebildet werden. Dafür gibt es 4 Möglichkeiten. Beim zweiten Fall muss es zwei Pärchen bei 4 Zahlen geben. Dafür gibt es 6 Möglichkeiten, aber da die Fälle,wie “1 und 3, und 3 und 1 bilden ein Paar” gleich sind müssen wir die 6 noch durch 2 teilen. Es folgt: 6·5·(4 +6/2) = 210"

Mir ist jetzt unklar, warum 6 durch 2 geteilt werden muss. Wir haben doch 6 Fälle. 1 und 2 bilden auf diesselbe Zahl ab

1 und 3 bilden auf diesselbe Zahl ab

1 und 4 bilden auf diesselbe Zahl ab

2 und 3 bilden auf diesselbe Zahl ab

2 und 4 bilden auf diesselbe Zahl ab

3 und 4 bilden auf diesselbe Zahl ab

=> 6 Möglichkeiten

Jetzt steht aber im Text "Fälle wie 1 und 3 und 3 und 1 bilden ein Paar" müssen gestrichen werden.

Und daraus würden dann 6 / 2 Möglichkeiten resultieren.

Aber die 6 Möglichkeiten waren doch nur (1,2), (1,3), (1,4). (2,3), (2,4) und (3,4). Da war doch diese Doppelung (1,3) und (3,1) gar nicht enthalten.

Oder meinen die damit, dass man die Fälle, dass z.b. (1,3) auf die Zahlen (3,1) abgebildet werden, streichen muss? Dann müssten aber auch alle Fälle wie (1,2) bilden auf (2,1) ab u.s.w. gestrichen werden und nicht nur die Hälfte?

Nehmen wir mal an, die erste getroffene Zahl in der Bildmenge wäre die 5 und die zweite getroffene Zahl in der Bildmenge wäre die 6. (Klappt natürlich auch mit 3 und 4 oder 1 und 2 als getroffene Zahlen in der Bildmenge.

Komme trotzdem auf 6 Fälle

was meinen die mit mit "1 und 3 bilden ein Paar und 3 und 1 bilden ein Paar" Meinen die ein Paar in der Bildmenge? Oder das 1 und 3 und 3 und 1 auf diesselbe Zahlen abgebildet werden? Wie genau sehen diese 6 / 2 = 3 Fälle eigentlich aus?

Mit gräulichen Füßen,

Hallo,

ist die Menge aller Teilmengen von den Natürlichen Zahlen abzählbar unendlich ?

Wenn ja wie kann ich es beweisen ?

kann mir jmd erklären welche von den unten genannten was sind und wieso?

A=[-3,0 [U] 0,1]

B=]-unendlich, 3[

C= {0} U {e^-n I n element aus N}

Hallo,

ich stehe hier vor einer vorgerechneten Aufgabe:

Ich verstehe nicht ganz, wie ich so etwas einzeichne.

Kann mir das jemand erklären?

Danke im Voraus.

LG

Soll man einfach nachweisen das die Klammer bei der Schnittmenge und Vereinigung irrelevant ist?(bei b)

Also das wurde heute nebenbei mal von meinem Dozenten erwähnt, aber trotz langem Überlegen verstehe ich nicht ganz genau, warum das so ist. Denn wenn eine Menge leer ist bzw. sie nichts enthält, wie kann sie dann Teilmenger einer anderen (bzw. jeder) Menge sein?

Es seien 𝑋𝑋, 𝑌𝑌 und Z Mengen sowie 𝑓𝑓:𝑋𝑋 ⟶ 𝑌𝑌 𝑢𝑢𝑢𝑢𝑢𝑢 𝑔𝑔: 𝑌𝑌 ⟶ 𝑍𝑍 Funktionen. Weiter sei ℎ ≔ 𝑔𝑔 ∘ 𝑓𝑓 die Komposition von 𝑓𝑓 𝑢𝑢𝑢𝑢𝑢𝑢 𝑔𝑔. Widerlegen Sie die folgenden falschen Aussagen durch je ein Gegenbeispiel. (a) Ist ℎ injektiv, so ist auch 𝑔𝑔 injektiv. (b) Ist ℎ surjektiv, so ist auch 𝑓𝑓 surjektiv. (c) Ist ℎ nicht injektiv, so gilt: 𝑓𝑓 ist nicht injektiv und 𝑔𝑔 ist nicht injektiv. (d) Ist ℎ nicht surjektiv, so gilt: 𝑓𝑓 ist surjektiv und 𝑔𝑔 ist nicht surjektiv.

Ich verstehe nicht, wie genau ich diese Aufgabe angehen soll. Kann mir jemand vielleicht wenigstens für eine Aufgabe den Lösungsweg geben, damit ich es nachvollzeihen kann?

wenn ein Alphabet Sigma endlich ist , was bedeutet das für die Mächtigkeit von Sigma Stern

Meine vermutung ist , dass Sigma Stern dann abzählbar unendlich ist aber wie kann man das beweisen und stimmt die Vermutung überhaupt?

Danke

Hey ich bin gerade am Verzweifeln bei der Aufgabe,

wir hatten das nur einmal kurz im Unterricht als Übung und dann aber nie wieder, es wurde auch nicht wirklich erklärt wie wir zur lösung kamen sondern nur einmal vorgerechnet und mehr nicht.

Kann mir vielleicht wer verraten wie ich da zu einer Lösung komme, bzw was ich denn überhaupt machen soll ???

Würde mich sehr freuen wenn mir das mal einer erklärt oder vllt einen link schickt wo das erklärt wird... ich habe dazu leider nichts finden können.

Hallo, was ist der Unterschied zwischen A ⊆ B und A ⊂ B? Ich hoffe, ihr könnt mir helfen ;)

Danke

Wieso gilt die eine Aussage und die andere nicht. Könnte vielleicht jemand für x Beispiele einsetzen und schrittweise durchgehen warum die Aussage für das Eingesetzte gilt oder warum nicht?

Kann mir jemand sagen ob das stimmt?

Und ich hätte eine frage bezüglich b) und zwar weiß ich das man die rechte seite ja genau so zeichnet wie die linke aber ich verstehe nicht warum? Kann man das irgendwie in worten leicht ausdrücken wie diese menke definiert ist?

und bei d) warum ist die menge hier gleich obwohl b ja auch eingezeichnet ist?!
Danke schon im voraus😊

Für eine nichtleere Menge Ω und eine Teilmenge A⊆Ω ist die Komplementärmenge Ac (auch kurz das Komplement Ac), definiert als Ac= Ω\A={ω∈Ω|ω /∈A}.Für eine beliebige, nichtleere Indexmenge I und Teilmengen Ai⊆Ω für i∈I ist die Vereinigung definiert als ⋃i∈IAi:={ω∈Ω|∃i∈I:ω∈Ai}.

Ist das also die Menge die alle Elemente enthält, die in der Menge Omega selbst enthalten sind oder in einer Teilmenge von Omega?

Danke im Voraus

Ich bin hier etwas verwirrt, weil ich kann leider nirgendswo finden, wie die Operatoren genau geklammert werden, d.h. welche stärker und welche schwächer bindet. Aus der Aussagenlogik ist mir folgende Reihenfolge bekannt, die auch überall zu stimmen scheint:

1. Negation
2. Konjunktion
3. Disjunktion
4. Entweder-Oder
5. Implikation
6. Äquivalenz

Wie sieht es jetzt aber in der Prädikatenlogik aus? Binden hier der Allquantor und der Existenzquantor jetzt stärker als die Negation oder schwächer als die Äquivalenz? Ich hoffe jemand weiß hier von einer einheitlichen Definition.

Kann mir jemand die folgende Aufgabe erklären? Stehe voll auf der Leitung.

Guten Tag!

Sei A=(a,b] das halboffene reelle Intervall mit a<b, in welchem das a aber nicht das b enthalten ist. Jetzt frage ich mich, ob dieses Intervall als offene oder abgeschlossene Teilmenge der Reellen Zahlen eingestuft werden kann. Für abgeschlossen habe ich eine Begründung und für offen auch. Nur bei offen bin ich mir nicht ganz sicher ob das so hin haut, wie ich mir das denke.

Also. Zunächst sei Br(x) eine offene Umgebung um x mit dem Radius r>0. Dann ist eine Teilmenge V eines Metrischen Raumes X offen, wenn für alle x0 aus X gilt, dass ein r existiert, sodass Br(x0) Teilmenge von V ist. Dies ist hier ja offensichtlich nicht der Fall. Wenn ich nun b=x0 wähle, ist für jedes r>0 die Umgebung Br(b) nicht Teilmenge von A=(0,1]. Somit müsste A ja abgeschlossen sein, denn wenn sie nicht offen ist muss sie ja abgeschlossen sein. ABER: In meinem Skript steht als Definition:

1. Eine Teilmenge V von X heißt offen, wenn [...] gilt.
2. Eine Teilmenge W von X heißt abgeschlossen, wenn X\W offen ist (X\W ist das Komplement von W)

Wähle ich nun als unseren Metrischen raum das reelle Intervall B=[a-1,b] ist A Teilmenge davon. Nun folgende Argumentation:

B\A=[a-1,a] ist offensichtlich abgeschlossen. Daraus folgt laut des zweiten Teils der Definition, dass A offen ist.

Ich habe gelernt, dass die leere Menge und R selber offen und abgeschlossen zugleich sind, jedoch nicht, dass gleiches für Halboffene Intervalle gilt.

Aufklärungsbedarf! Ich würde mich über eine kurze Antwort auf die Frage im Titel und eine kurze Begründung freuen! Hinweise auf Fehler in meiner Argumentation würden ich auch begrüßen

Danke und LG

Max Stuthmann

Guten Tag:

Seien I_n mit n aus N nichtleere abgeschlossene Intervalle in R, sodass I_(n+1) teilmenge von I_n ist. Dann ist der Schnitt dieser Intervalle (für n=1 bis unendlich) nicht leer.

Okay, das mag ja sein, aber hier steht, es gilt NICHT für offene Intervalle und wir sollen uns da mal ein Beispiel überlegen. Aber wieso gilt dies denn nicht für offene Intervalle und hätte jemand da n Beispiel?

Danke und LG Max Stuthmann

Guten Tag

Ich wollte mal nachfragen ob ich die folgende Aufgabe richtig gelöst habe ? (punkte a und b)
Wäre für jede Hilfe sehr dankbar LG

Hallo,

kurze Frage:

Wenn V offen ist und

wie kann ich zeigen dass U auch offen ist? Folgt das direkt?

(M ist Teilmenge X und (X,d) ist metrischer Raum)

Die Aufgabe heißt "Wieviele Teilmengen hat eine Menge mit 2, 3, 4, 5, 6, n Elementen"

Ich weis nicht ob die aufgabe leicht ist oder ob ich einfach zu blöd dafür bin

Wäre euch wirklich dankbar falls mir einer erklärt wie man bei dieser aufgabe auf ein ergebnis kommt :)

Hi,

wieso ist

weder weder abgeschlossen noch offen. Dass sie nicht offen ist, kann ich gar nicht nachvollziehen, schließlich liegen ja ihre Randpunkte, also 2 und 17 nicht mehr in der Menge selber. Aber wie kann sie dann ebenfalls nicht abgeschlossen sein? Das ergibt für mich gerade irgendwie überhaupt keinen Sinn.

VG:)

Eine dreiköpfige Familie isst an einem quadratischen Tisch. Sie wechseln jeden Abend die Plätze, um alle Sitzordnungen auszuprobieren. Wie viele Tage brauchen sie?

Was ändert sich bei 4 Personen?

Was ändert sich bei 5 Personen an einem Tisch für 6 Personen?

Eine Implikation (also => ) bedeutet ja so viel wie wenn...,dann.... gilt das aber auch umgekehrt. Also Beispiel 2x => 4 würde dann auch gelten 4=> 2 x

Hallo! Bei diesen Aufgaben stehe ich leider irgendwie total auf dem Schlauch :( kann mir da jemand weiterhelfen? Danke im Voraus !





Falls euch das eine Zeichen nicht angezeigt wird, das ist ein "Element aus". Vielen Dank im voraus für eure Hilfe!

Hat jemand eine Ahnung was genau damit gemeint ist? Ich schreibe bald eine Matheprüfung, und das ist eine der Übungsaufgaben die ich zur Vorbereitung machen wollte.

Was bedeutet das "max" vor der Mengenklammer? Und kann mir jemand vielleicht umgangssprachlich erklären, was da genau bewiesen wird? Ich komm nicht drauf...

Weiß jemand, wie man das darstellen kann?

Menge aller dreistelligen Dezimaldarstellungen natürlicher Zahlen ohne führende Nullen

Hey zusammen,

ich habe eine Frage zu den beiden Aufgaben, und zwar, wie zeige ich an, dass die Nullstellen des Polynoms achsensymmetrisch sind?

Und wie bestimme ich die Inverse von der Menge F3(+) und F3(*)?

Hallo, ich benötige hilfe beim lösen der folgenden Aufgabe. Ich habe mir mehrmals die Vorlesungsfolien durchgelesen, aber komme trotzdem kein Prozent weiter.

Auf N(natürliche Zahlen) sei folgende Relation gegeben:

n~m:⇔n

und m

 haben einen gemeinsamen Teiler verschieden von 1.

Überprüfen Sie, ob es sich um eine Äquivalenzrelation handelt und geben Sie gegebenfalls die Äquivalenzklassen an.

Ich habe folgendes schon gemacht(siehe Foto) ist das sogar eventuell richtig?

würde mich sehr über eine Lösung freuen, da ich diese Punkte für die Hausaufgaben benötige..

Danke ich vorraus für jede Antwort.

A = { {},1}

Was ergibt A \{} = ?

Wenn a ein Element der Äquivalenzklasse [x] ist und auch von [y], wieso muss dann [x]=[y] sein?

Was bedeutet bei einer Ordnungsrelation das geordnete Paar (X,R), wenn die Relation R auf def Menge X ist? Was ist dieses Paar und warum schreibt man dieses auf?

Hallo. Habe gerade einen Beweis hinter mir. Man sollte zeigen, dass eine n-elementige Menge M genau n über k Teilmengen mit k Elementen besitzt.

Nun heißt es in der folgenden Aufgabe: "Nutzen Sie das vorherige um die Anzahl der Teilmengen festzustellen".

Ich bin verwirrt.. das wären halt n über k Teilmengen!? Oder was ist hier gemeint? Bild ist angefügt.. es geht also um (b)

A:={1,5,6} B:={2,4,7}

P ((A \{5} ) x (B \{4} ))

Dies war meine Idee:

P:={{1,2},{1,7},{6,2},{6,7},{1,6},{2,7}

wäre das so korrekt?

Wie soll man den da etwas finden? Es soll ja zu jedem y-Wert mind. ein x-Wert geben. Würde problemlos klappen. Aber wie kann die dann surjektiv sein? ist doch unmöglich, oder? Das Problem ist, dass nur natürliche Zahlen erlaubt sind.

hoffe mir kann jemand weiterhelfen

Habe diese Aufgabe und ich glaube ich habe da ziemliche Scheisse hingeschrieben, oder?

Beweisen soll ich die Mengengleichheit, die ich rot unterstrichen habe

Gibt es hier kluge Köpfe?

Wie negiere ich eine Vereinigung in einer Aussage z.B.: A geschnitten B = {} wobei A und B Mengen sind.

Hallo,

ich komm leider einfahc nicht weiter. Ich verstehe alle Symbole von Mengen etc. Aber ich versteh nicht ganz was dieses p und q teilerfremd bedeuten soll.

Heißt es einfach dass wenn 3 unten steht dann darf oben nicht 6, 9 etc stehen oder wie?

Hallo liebe GF-Community!

Vorhin habe ich eine Frage zu Urbildern und Umkehrfunktionen beantwortet und dabei kam mir selbst eine Frage in den Kopf: Was, wenn ein Symbol in einem Ausdruck sowohl als Urbild als auch als Umkehrfunktion interpretiert werden kann? Gibt es eine Präzedenzregel oder muss man stets explizit dazuschreiben, was das Symbol bedeutet?

Um die Frage etwas zu veranschaulichen: Definiere eine Menge

 und eine Funktion



Nun ist diese Funktion bijektiv, besitzt also eine Umkehrfunktion. Für gewöhnlich werden Umkehrfunktionen und Urbilder beide mit f^(-1) dargestellt. Was aber bedeutet dann der Ausdruck

 Erste Möglichkeit (f^{-1} als Umkehrfunktion):

 Zweite Möglichkeit (f^{-1} als Urbild):



Die beiden Ergebnisse sind offenbar verschieden. Gibt es hier eine Konvention?

Wenn da zB. steht :A ist die Menge aller Asiatischen Länder, dann sind da ein paar Länder aufgelistet, aber manche sind nicht zugehörig,dann ist es kein Element von Menge A, aber wie schreibt man das auf? Und muss etwas in eine Klammer?

Hallo, ich bin eben auf folgende Aufgaben gestoßen und weiß nicht, was dieser Strich über den Buchstaben heißen soll. (Siehe Bild)

lg

Meine Kollegen kommen auf ein ganz andere Lösung, was mich natürlich irritiert. Deshalb wollte ich fragen, ob meine Lösung richtig ist, ich habe es mehrmals durchgerechnet? Besten Dank.

Ich versuche zurzeit im Rahmen meiner Klausurvorbereitung folgende Aufgabe zu lösen:

1. Sei A eine überabzählbar unendliche Menge und die Menge B ⊂ A abzählbar unendlich. Die Menge A \ B ist immer überabzählbar.
2. Jede nicht endliche Teilmenge einer abzählbar unendlichen Menge Teilmenge ist abzählbar unendlich.

Diese Aussagen sollen bewiesen werden. Ich weiß irgendwie nicht wie ich da rangehen soll, vielleicht per Beweis per Widerspruch. Wenn jemand zumindest einen Ansatz hätte würde mir das schon helfen.

Bin jetzt an einer Mengenlehre Textaufgabe dran, aber irgendwie komme ich nicht auf die gelb markierten Stellen bzw auf die 18 vor allem.

Es steht, dass Kenntnisse in Administration und Verkauf 24 Personen haben und 8 Personen DAVON auch im Verkauf. Sprich: die 8 Personen haben von allen 3 Bereichen Kenntnisse. Jedoch, wie auf dieser Welt kommt er auf 18?? Also E geschnitten mit A??

Hallo

Ich habe eine Übungsaufgabe wo ich Beweisen muss, dass die Menge der natürlichen Zahlen gleichmächtig zu der Menge der ganzen Zahlen ist.

Sowie die Menge der ungeraden zu den Gerade Zahlen gleichmächtig ist.

WIe wird sowas im Detail gemacht? Durch einen sogenannten "direkten Beweis" ?

LG

Wir haben gelernt, dass jeder Körper Nullteilerfrei ist.

Nullteilerfrei bedeutet: Es darf nicht vorkommen: x≠0≠y wobei xy=0.

Wenn ich jedoch in F4 2*2 rechne, kommt 0 raus. Somit nicht Nullteilerfrei, somit wär‘s auch kein Körper.

Kann mir wer erklären was ich falsch mache??

Sqrt(3) ist ja nicht in den Rationalen Zahlen enthalten, aber z.B. 2 ist trotzdem eine obere Schranke der Menge in den Rationalen Zahlen. Aber was ist dann die kleinste obere Schranke, wenn es nicht sqrt(3) ist ?

Gehen wir mal von dieser injektiven Umkehrabbildung aus:

N→N, x↦3x+2

Wie gehe ich vor, wenn ich davon die linksseitige Umkehrabbildung bilden möchte und in wiefern unterscheiden sich links- und rechtsseitig?

Bonus: Weshalb zeigt solch eine Umkehrfunktion überhaupt ob eine Abbildung surjektiv bzw. injektiv ist?

Hallo

ich bräuchte einmal Hilfe bei einer Aufgabe da ich absolut nicht weiterkomme.

Aufgabe:

Sei f : [2,∞) → R, f(x) := √x−2. Schränken Sie Definitions- und Wertebereich so ein, dass f bijektiv ist (mit Beweis). Bestimmen Sie die Umkehrabbildung f−1 (mit Beweis).

Vielen Dank schonmal im Voraus.

Wenn der Lehrer verlangt: Menge der natürlichen Zahlen zwischen 3 und 11.

Sind dann die Zahlen 3 und 11 dabei oder nicht? Gibt es für das Wort "zwischen" eine verlässliche Definition?

Hallo Freunde, ich muss die gegebene Menge ( siehe Bild) als Vereinigung von Intervallen darstellen. Jedoch weiß ich absolut nicht wie das geht. Könnt ihr mir weiterhelfen

Untersuchen Sie die folgenden Mengen unter Verwendung von A = B ⇔ (A ⊂ B) ∧ (B ⊂ A) für zwei Mengen A und B auf Gleichheit:

(i) A = {z ∈ Z | es existiert ein m ∈ Z mit z = 7m + 4}, B = {z ∈ Z | es existiert ein m ∈ Z mit z = 7m − 3},

(ii) A = {z + z 0 ∈ Z | z, z0 ∈ Z}, B = {2z ∈ Z | z ∈ Z},

(iii) A = {(x, y) ∈ Q × Q | x + y = 3 und x − y = −5}, B = {(−1, 4)}.

Ich habe keine Ahnung wie ich bei solchen Aufgaben vorgehen muss. Könnt ihr mir für den Anfang helfen

Wie nennt man die obige Zahlenfolge?

ich muss als Hausaufgabe folgende Mengengleichheit zeigen:

u: Vereinigung

$: Schnittmenge

(AuB) $ (AuC) $ (BuC) = (A $ B) u (A $ C) u (B $ C)

Ich weiß einfach nicht, wie ich anfangen soll, ein Ansatz oder irgendeine Idee würden mir schon helfen. Ich würde mich riesig über jegliche Hilfe freuen.

Hallo zusammen,

bei meinen Wochenaufgaben stehe ich grade auf dem Schlauch. Die Aufgabe lautet:

Bestimme eine Formel mit der die Anzahl der zweielemetrigen Teilmengen einer beliebigen Menge mit n Elementen berechnet werden kann.

Ich weiß absolut nicht was gemeint ist, ihr müsst mir das Ergebnis auch nicht vorsagen, würde mich nur über einen Lösungsansatz freuen. Danke im Vorraus

Hallo liebe Community,

es geht um die Frage: "Wie viele Teilmengen hat eine 10-elementige Menge insgesamt?" beziehungsweise den Lösungsweg meines Lehrers dazu.

Ich habe dies so berechnet: (10 über 0)+(10 über 1)+(10 über 2)+(10 über 3)+(10 über 4)+(10 über 5)+(10 über 6)+(10 über 7)+(10 über 8)+(10 über 9)+(10 über 10) = 1024

Mir ist klar, dass dies sehr aufwändig ist, gerade die Frage zu einer 100-elementigen Menge gestellt worden wäre...!

Wie im Folgenden zu sehen hat mein Lehrer uns dann einen sehr einfachen Lösungsweg für diese Aufgabenart gezeigt:

Mithilfe (a+b)^n mit n=1; 2; 3; 4; 5;... haben wir uns das Pascalsche Dreieck aufgezeichnet, was ich auch noch verstehe.

Nur den Schritt, der darunter kommt, verstehe ich absolut nicht mehr [(1+1)^10], deshalb diese Frage. Mein Lehrer meinte, man könne in solchen Fällen einfach mit 2 hoch der n-elementigen Menge rechnen und komme so zum Ergebnis.

Kann diesen Gedankengang jemand kommentieren und mir verständlich machen, wieso das gilt?!

Vielen Dank im voraus und Grüße carbonpilot01

Ich komme auf dem Foto mit der Aufgabe 1b) nicht klar. Laut Aufgabenstellung soll ich die Menge von der beschreibenden in die aufzählende Form umwandeln. Wie finde ich für n alle natürlichen Zahlen, die 120 teilen? Gibt es da einen Trick oder muss man sich für jede Zahl überlegen, ob sie 120 teilt? Das dauert doch viel zu lange.

Also genau die Frage wie in der Überschrift.

Bild sagt nochmals die Aussage aus. Ist die richtig oder falsch?

Hallo,

ich studiere derzeit Informatik und habe grad etwas was mir seit Stunden die Nerven zereißt. Und zwar steht im Skript unter "Ordnungsrelation":

"Hat man eine Ordnungsrelation (kleiner gleich) auf einer Menge X, so kann es immer noch sein; dass es Elemente x, y aus X gibt, die unvergleichbar sind, für die also weder x (kleiner gleich) y noch y (kleiner gleich) gilt."

Was ich daran jetzt net verstehe. Wie kann ein Tupel nicht x (kleiner gleich) y noch y (kleiner gleich), weil jedes Tupel wie Bsp (1,2) erfüllt doch die Bedingung, genuso wie (1,1) etc... ich krieg es einfach nicht verstanden. Ich hoffe jemand kann es mir etwas verständlicher erklären.

Kann mir wer bitte die Aufgaben erklären? Muss ich bei der ersten Aufgabe zahlen einsetzen oder wie? Und die letzte Aufgabe verstehe ich garnicht. Bitte um dringende Hilfe , da das Thema wiederholt wird, ich dieses aber nie hatte.

Ich muss die Beziehung zwischen A und B audrücken mit der gegeben Gleichung: A \ B = A' Die Lösung ist A=B=G G steht für Grundmenge. ich verstehe wirklich nicht, wie eine Menge ohne sich, die Komplementmenge sein kann. Kann es mir bitte jemand erklären?

Das ist die Aufgabe, aber meine einzige Frage ist: was sind 6-stellige Zahlen des Zehnersystems?😂