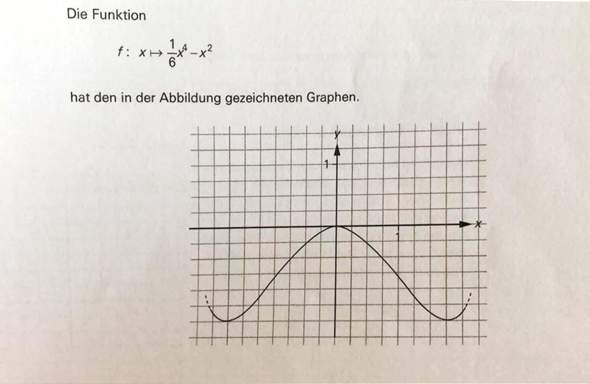
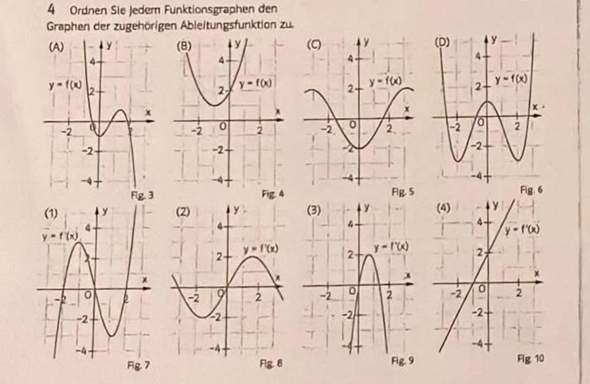
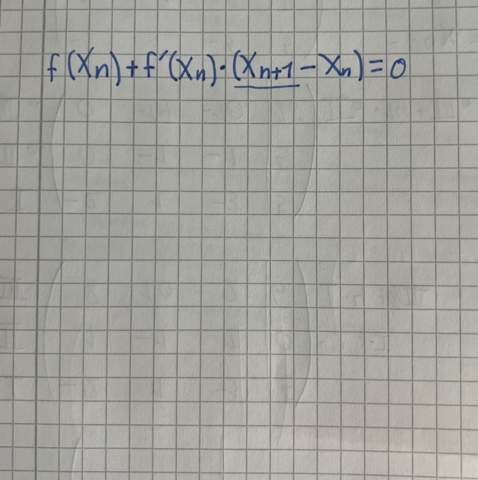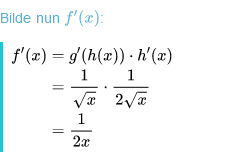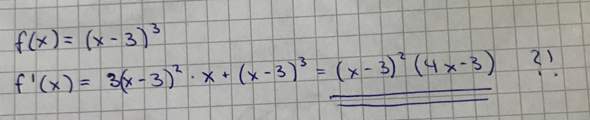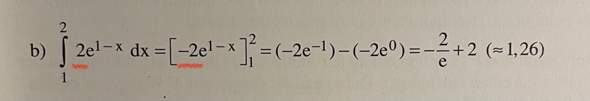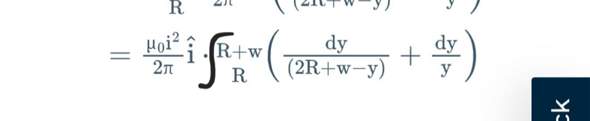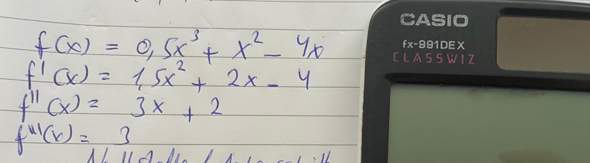f(x) = x^3 auf Definitionsbereich IR d. h. ]-unendl., + unendl.[

f'(x) = 3x^2 f'(x) = 0 für x = 0

Für die Intervalle

]-unendl, 0[ und ]0, + unendl[ ist

f'(x) streng monoton steigend

der Graph von f steigt immer außer für x = 0

So, hier liegt nun kein VZW für f'(x) bei x = 0 vor, d. h. es gibt kein lokales Minimum oder Maximum. a) Richtig?

Laufe ich nun gegen die Randpunkte

lim x -> minus unendlich kommt minus unendlich heraus

lim x -> plus unendlich kommt plus unendlich heraus

Dies heißt nun, dass der Graph kein globales Minimum oder globales Maximum auf den Definitionsbereich IR besitzt, da die Randpunkte ja gegen minus und plus unendlich gehen.

b) Richtig?

Wie man auf die Ableitung kommt ist nachvollziehbar.

Könnte man hier den die Ableitung nicht noch weiter vereinfachen?

Wurzel (1 - sin²(x) ) ist doch das selbe wie Wurzel(cos² (x)) = cos(x) und somit -cos(x) / cos(x) = -1?

Hey! Ich muss diese Gleichung (siehe Bild) nach Xn+1 umstellen komme aber nicht drauf. Könnte mir bitte jemand diese inkl. den einzelnen Schritten unstellen?

Vielen Dank schonmal!

Begründen Sie, weshalb die relativen Extrempunkte des Graphen von f nicht absolut sein können.

Über die Anwendung weiß ich schon länger bescheid. Ich mag es aber nicht so gerne, Konzepte anzuwenden, die ich nicht zu beweisen vermag.

f(x)= -2e^-4

Wichtig für mich ist hier, dass 2 mal Minus da steht, weil irgendwie in der Lösung noch ein x drangehängt wurde und das verstehe ich nicht.

das steht ja fest das 1 raus kommt

was ist aber cos(a)*sin(a) gibt es da auch so ne regel ?

Also wie kommt man auf A und B? Ich denke das, was ich da gerechnet hab ist falsch

geg. an = 1/n × cos(n)

Man sieht sofort, dass es eine Nullfolge ist. Die Cos. Funktion alterniert und 1/n geht gegen 0. Aber kann man das auch fundiert beweisen?

Sowohl bei der Berechnung von extremstellen als auch bei wendestellen . Gibt's hinreichende Bedingung einmal f"(x)≠0

Und bei wendestellen f'''(x)≠0

Kann mir jemand erklären warum das sein muss?

Guten Abend,

es geht um die hell blau markierte Gleichung rechts im Bild.

Der Gradient von f in p = 0 (Nullvektor) hat doch in jeder Komponente den Grenzwert, wie er unten links (dunkel blau markiert) steht - das sind ja gerade die partiellen Ableitungen.

Wenn man nun mit das Skalarprodukt aus dem Gradienten und dem Vektor a bildet, erhält man aber immernoch null und nicht 1/(3*sqrt(3)).

Ich verstehe zwar, dass die Ableitung in Richtung a eigentlich 1/(3*sqrt(3)) ist, aber nicht, wieso diese Formel gilt.

Kann mir die jemand erklären - vielleicht verstehe ich ja auch nur die Notation falsch?

Könnte mir jemand diese Funktion einmal nach x und einmal nach y partiell ableiten?

Hallo Zusammen;

ich verstehe bei Folgender Aufgabe die d) nicht.

Es geht wohl um eine Differenzfunktion, von der man dann die Ableitung machen soll . Ich verstehe das aber absolut nicht.

Könnte mir jemand eine detaillierte Antwort geben?

Dachte eigentlich ich bin mit der partiellen Integration auf dem richtigen Weg, aber kurz vor dem Ende hab ich ja wieder eine Funktion die ich nicht integrieren kann :(((

Hallo liebe Freunde der Mathematik,

Bei mathematischen Blödeleien stieß ich auf die Funktion floor(|sin(x)|). Also der Betrag ses Sinus, aber auf die nächstkleinere ganze Zahl abgerundet. Da der Sinusbetrag nur Werte zwischen 1 und 0 annimmt, lassen sich hier zwei jeweils unendlich mächtige Mengen definieren:

M1{x: floor(|sin(x)|)=1}

Diese Menge ist unendlich groß und erfüllt für alle x=(2k+1)/2*π.

M2{x:floor(|sin(x)|)=0}

Diese Menge ist unendlich groß für alle x≠(2k+1)/2*π.

Die erste Menge ist relativ offensichtlich abzählbar zu den natürlichen Zahlen, da man jedem x0 eine natürliche Zahl zuordnen kann und andersherum.

Da ich aber jedem x0 aus M1 nur ein x0 aus dem jeweils schräg links unterem Bereich aus M2 zuordnen kann, muss M2 doch eine größere Unendlichkeit als M1 und damit überabzahlbar bzgl. den natürlichen Zahlen sein.

Stimmt diese Argumentation? Ist floor(|sin(x)|) damit eine Analogie zu Hilberts Überlegungen an sich?

Vielen lieben Dank für Antworten und eure Aufmerksamkeit :)

Hi, ich verstehe nicht ganz, wie man bei Taylorreihen bestimmt, dass der Rest der Reihe für n gegen unendlich gegen 0 konvergiert. Ich habe das Beispiel der Funktion f(x) = ln (1 + x), Entwicklungspunkt: x = 0 und das Intervall I (-0,5, 1]. Es ist nicht gegeben welchen Grad die Reihe haben muss, also habe ich Grad 3 genommen. Dann bekomme ich: x - 0,5 x^2 + (1/3) * x^3 + R. Nun muss ich noch den Rest R bestimmen und herausfinden ob dieser für n gegen unendlich gegen 0 konvergiert. Dafür hat man die Formel lim n gegen unendlich R(x) = (f^(n+1)(xi) / (n+1)!) * x. Wie gehe ich nun weiter vor??

Guten Tag,

ich benötige bei dem Aufgabenteil a) und b) noch etwas Hilfe, um das verstehen zu können. Aufgabenteil c) und d) verstehe ich perfekt. Hier die Aufgabe:

Hier weitere Fragen von mir:

• Wann ist F(x) am größten in Bezug auf die Funktion f(x)?
• Wann ist F(x) am kleinsten in Bezug auf die Funktion f(x)?
• Was sagt F(x) im allgemeinen aus im Vergleich zu f(x)?

Ich freue mich sehr über hilfreiche Antworten

Hallo zusammen, ich bin grad in der elften Klasse eines Gymnasiums und wir haben in Mathe gerade Extremwertprobleme. Normalerweise bin ich super in Mathe und hab auch bei dieser Art von Aufgabe eigentlich nie sonderliche Probleme, aber ich komme leider einfach nicht auf eine gescheite Lösung. Vielleicht könnt ihr euch die Aufgabe/meinen Lösungsansatz mal anschauen und mir sagen worans gelegen hat? Liebe Grüße

Hi, kann mir jmd helfen bei di

eser Funktion die Nullstellen zu bestimmen?

Danke für eure Hilfe!

was genau ist in diesem Schritt passiert?

Wenn ich das integral einer Funktion f, die unterhalb der X Achse verläuft, zum Beispiel im Intervall 0-1 bestimmen möchte, muss ich dann vor das integral ein minus setzen oder wird das integral automatisch negativ?

Danke für eure Hilfe!

Wie beweise ich, dass

x-x^3/3!+x^5/5!-x^7/7! ...

periodisch ist?

Woher kommt in der Ableitung der Inhalt der ursprünglichen Klammer (x² - 3) und die Ableitung dieser (2x)?

Hi,

ich verstehe die 11 c nicht, wie soll ich da rausfinden wann es auf 380m fliegt?

in den Lösungen steht bei 60s aber ich verstehe nicht wie man darauf kommt

Wie kommt man hier auf den Exponenten 5/2?
Bei mir kam ich bis zu -6 / ( 2 * sqrt(2x^-3 * x^4) ), dann dachte ich dass ich die Exponenten einfache addieren kann(weil gleiche Basis) und somit -6 / ( 2* sqrt(2x) ) hätte..

Es geht um das erweitern und umstellen von Bruchtermen!

Bei Bruchgleichungen multipliziert man den Hauptnenner der Brüche mit dem Zähler und im Nenner.

Bei Bruchtermen die man z.B. miteinander addiert, erweitert man die jeweiligen Bruchterme nur um das, was bei dem jeweiligen Bruchtermen fehlt, also z.B. Bausteine des Hauptnenners wie [x], [x+5], also Hauptnenner = x(x+5).

Ich hoffe es ist nicht so kompliziert formuliert...

Hi ich hab morgen in Mathe mündliche Prüfung und über gerade. Und da ist mir eine komplette Aufgabe begegnet, die mir sehr schwer fällt.

Kann mir jemand bitte helfen und diese Aufgaben für mich lösen? Ich bin gerade bisschen aufgeschmissen und es gibt leider keine Lösungen dazu.

Explizit geht es um die Aufgaben Punkte 2, 3, 4 & 7

Vielen dank schonmal 🙏🏼

LG

Hallo,

ich möchte gerne folgende Funktion nach y ableiten



Die Lösung habe ich, die lautet

 kann mir bitte jemand die Schritte erklären, wie ich auf die -1/y komme?
Also gibs da einen Tipp über Umschreiben oder so?

Also mir ist bewusst, dass ln zu 1/x wird. aber wird das y nicht irgendwie zu y^2???

Rw, ges = - 10 log (( 1/15 (8,7 x 10 hoch -55/10) + (2,8 x 10 hoch -25/10) + (3,5 x 10 hoch -40/10))

Kann man am Taschenrechner ein Abstand zwischen zwei Zahlen machen, wenn er immer falsch rechnet.

Kann mir jemand bei dieser Matheaufgabe helfen? Den Graphen habe ich schon gezeichnet, aber ich weiß nicht, wie das Dreieck aussieht.

Gegeben ist die Funktion f mit f(x)=-(x-4)^2+4. Der Punkt P(x|f(x)) liegt im Intervall [2; 6] auf dem Graphen von f. Die Parallele zur y-Achse durch P schneidet die x-Achse im Punkt Q. Mit R (6|0) bilden die beiden Punkte das Dreieck QRP.

a) Zeichnen Sie den Graphen von f im Intervall [2; 6] sowie ein mögliches Dreieck.

b) Berechnen Sie, für welches x der Flächeninhalt des Dreiecks maximal wird.

Ich soll bei der Funktion 400*1,5^x den Wert von x herausfinden bei 2025. Ich habe den Rechenweg den man auf dem Bild sieht angewendet und diesen haargenau von Studyflix kopiert, doch das Ergebnis sollte eigentlich 4 sein.

Was habe ich falsch gemacht?

Hi, ich weiß nicht was ich unter A‘ oder A Punkt verstehen soll. Was bringt einem das bzw was bedeutet es?

Ich muss als Hausaufgabe Funktionen mit Brüchen oder Wurzeln mit der Kettenregel ableiten, ich weiß aber nicht so ganz wie ich das machen soll. Es gibt bei der Kettenregel ja immer eine innere und äußere Funktion, aber welche ist bei einem Bruch oder einer Wurzel die innere und welche die äußere?

Vielen Dank im Vorraus

also vom 1. shcritt zum 2. der von 2. zu 3. ist ja klar aber von 1. zu 2. was wurde da angewandt

Hallo,

ein Online-Einstellungstest für einen Ausbildungsplatz für den Bankkaufmann beinhaltete folgende Aufgabe:

ein Symbol bedeutet, dass es sich um eine einstellige Zahl handelt (0-9) und zwei Symbole hintereinander sollen eine zweistellige Zahl darstellen (10-99).

Die einzige Aufgabe, die ich lösen konnte, war die zweite.

Danke!

Hey,

kann mir jemand eventuell bei der Aufgabe 5) weiterhelfen? Ich komme da überhaupt nicht weiter ?

Was ist mit der Maßzahl gemeint?

Das hat mein Mathelehrer angeschrieben. Wo liegt da der Unterschied beim ableiten beider Fälle? Es kommt doch beides auf dasselbe hinaus, oder? Wie kann eine Funktion, also g(x), im Exponenten einer Funktion sein?

Hallo ich weiß leider nicht, wie man das Ganze hier rechnet für die a) lediglich. Für die X-Achse habe ich y und z gleich 0 gesetzt. Doch wie rechnet man das Ganze. Kann mir jemand es einmal ausführlich vorrechnen mit einem LGS?

Ich schreibe morgen eine Matheklausur

Ja alsoo ich verstehe das nicht und was bedeuten eigentlich diese 2 Striche. Also der Betrag von -2 ist 2 weil das ist der Abstand zur Null das ist das einzige was ich kann. Jetzt sehe ich in meinen mathebuch diese Stiche |2| sowas und bin verwirrt

Hallo dieser Vektoren sollen parallel und identisch sein. Doch bei mir kommt ein Widerspruch raus. Was habe ich falsch berechnet?

Ich soll an Richtungvektor schauen ob es ein vielfaches gibt, um zu sehen, welche Geraden parallel zueinander sind. Ich dachte dass g parallel zu h wäre doch in den Lösungen steht das nicht. Aber 2 ist doch ein vielfaches von 8,-1 von -4 und 1 von 2. Ich habe das irgendwie Probleme mit der Methode. Doch die soll ich anwenden.

Hallo, ich schreibe morgen eine Mathe Arbeit u.a. Über die pq Formel. Nun habe ich mir die Frage gestellt, ob man bei den Brüchen in der Klammer den Nenner und den Zähler, oder nur den Zähler potenzieren muss.
liebe Grüße

Hallo,

wäre nett wenn mir jemand ein Beispiel hierfür geben könnte ich komm einfach nicht weiter. 😭

Sei f : ℝ → ℝ eine Funktion, die jeden Wert y ∈ ℝ genau zweimal annimmt. Zeigen Sie, dass f nicht stetig ist.

Hinweis: führen Sie die Annahme, f sei stetig, zu einem Widerspruch. Starten Sie dazu mit einem beliebigen y ∈ ℝ, wählen Sie zwei Punkte a < b mit f(a) = y = f(b). Betrachten Sie die beiden Fälle f((a+b)/2​ ) > y oder f((a+b)/2​) < y. Zeigen Sie für den ersten Fall, dass f(x) < y für alle x < a und alle x > b (Zwischenwertsatz), und folgern Sie daraus, dass f auf ganz ℝ nach oben beschränkt ist. Warum ist das ein Widerspruch?

Hallo,

ich hänge grade bei einer Aufgabe fest:

Ein Gerücht verbreitet sich und seine Momentane Änderungsrate (wie viele hören es stündlich) ist durch einen Graph dargestellt.
Wir sollen rechnerisch zeigen, dass die momentane Änderungsrate nach der Zehnten Stunde abnimmt.

Siehe Aufgabe d)

Soweit sogut.
Wir bekommen dafür eine Formel: f(t)=20t^2*e^-0,2t
Mit dieser sollen wir rechnerisch zeigen, dass die momentane Änderungsrate nach der 10ten Stunde abnimmt.

In den Lösungen ist folgender Rechenweg abgebildet:

Die ersten drei Zeilen leuchten mir ein, die drei folgenden jedoch kaum.

1. Wie kommt man dazu die „40t*e^-0,2t-4t^2*e^-0,2t“ in „4t*e^-0,2t*(10-t)“ zu verwandeln? (Wie wird hier vereinfacht!?)
2. Und warum ist das Ergebnis t>10 ein Beweis für das Abnehmen der momentanen Änderungsrate nach t=10?

Ich wäre für eine ausführliche Erklärung sehr dankbar!

Vielen Dank im Voraus! 🙏

Oder kann er auch woanders liegen?

Also z.b HP 4 und 2 und TP 0 und 0, wäre dann die Wendestelle genau be 2 und 1?

Oder kann es sein, dass er etwas weiter links oder rechts liegt?

Hey,

Kann mir eienr die Wendepunkte der funktion f(x)=¼x^4-2x^2 berechnen?

Ich habe P1(1,15/-2,2) und p2(-1.15/-2.2) raus, aber da skann ja nicht sein, weil es nicht genau in der Mitte zwischen Hoch und Tiefpunkt liegt, oder? (HP ist Ursprung, TP sind 2/-4 und -2/-4)

also irgendeine funktion

ich meine sowas wie

1/x --> ln(x)

1/(u^2+1) --> arctan(u)

was sind so die wichtigsten standardsachen, die man sozusagen einfach lernen muss?

An sich weiß ich wie es geht aber bei a hab uch keine Ahnung. Also die Nullstellen kann man ablesen aber was mavj ivh dann?

Anhand von diesem graphen? Ich dachte damit sind die y werte von f' gemeint beim x wert -2 und-1 aber dies scheint nd der fall zu sein

Ich lerne grade auf unsere Arbeit, iwi fällt mir aber nicht ein wie ich bei 5 nun die Extremstellen erkennen kann? Hätte ich die Funktion von f wär das kein problem aber ablesen fällt mir schwer, weil ich nicht weiß wie ich vorgehen soll... könnte mir jnd bitte helfen

Geht sowas

Vektor v = sinus(x)

cos(x)

1

Links und rechts natürlich die Klammern

Also statt irgendwelchen zahlen eine Funktion im Vektor.

Wenn ja wie kann ich mir sowas Geometrisch anzeigen lassen

Wir haben uns eine mal aufgeschrieben aber ich komm nicht mehr drauf

???

Wie kommt man auf das unten stehende Ergebnis?

Man muss doch (x * y) / (x² + y²) ableiten oder nicht?

Ich hänge an dieser Aufgabe fest. Ich habe den Punkt P(0|0) den HP(0|2) TP(-3|-2) und Q(-3|-2) ablesen können. Doch als ich vergleichen wollte stand bei der Lösung bei der III.) Bedingung f(-3)=…=-2 obwohl das ja der Tiefpunkt ist und er ja mit der 1. Ableitung gerechnet werden muss. Die IV.) Bedingung ist zwar mit der 1. Ableitung gemacht worden aber mit dem TP (-3|0). Da ist doch gar kein TP bei (-3|0)??? Was mache ich falsch 😅

Kann mir jemand helfen hier weiterzukommen?

Danke

Ich muss diese Aufgabe lösen, doch bekomme es nicht hin. Kann mir da jemand helfen und es Schritt für Schritt erklären?
Vielen Dank

Hallo,

wie zeigen ich mit Hilfe des Cauchy-Produkts, dass das Folgende für alle x, y ∈ R gilt??

cos(x + y) = cos(x) cos(y) − sin(x) sin(y).

wäre nett wenn mir wer helfen könnte.

Gruß

Hi,

Die Besucherzahl eines Zoos kann mit Hilfe der Funktion f(x) = - 10x^3+ 75x^2 ?

modelliert werden. x ist dabei die Anzahl der Stunden nach Öffnung des Zoos um 8:00 Uhr.

Berechne um welche Uhrzeit die meisten Besucher im Zoo ware n?

danke

Ich möchte berechnen wann in 90 Minuten etwas passiert.

das passiert in der ersten Minute zu 1/90 und dann in der nächsten mit 1/89 usw

wie kann ich das direkt berechnen?

wie ermittle ich die Funktion

Heyo,

Bei Vorbereitung auf eine Mathematik SA wollt ich zwei Übungen machen, die mir nun sehr schwer fallen.

1) Ermitteln sie Art und Lage der Extremstellen von f. Geben Sie auch die Punktkoordinaten an.

f(x) =x³ - 3x² + 3x - 1

2) Bestimmen Sie die Wendepunkte der Graphen der gegebenen Funktionen. Geben Sie auch das Krümmungsverhalten an.

f(x) = ⅛x⁴ - 3x²

Herzlichen Dank 🙏

Moin freunde,

kann mir jemand meinen Denkfehler erklären?

1. Partielle Ableitung der funktion: 3*x^3*2*y^2

y^2 bleibt unsere konstante, somit rechne ich das hoch im x mal 3 und mal 2

9x^2+6y^2

ODER bleibt 2y^2 konstant? also 9*x^2*2*y^2

Ich hoffe es war verständlich und danke im Voraus

hi, kennt jemand ein programm für den ti 84 plus, was dafür sorgt, dass der taschenrechner ableitungen bestimmen kann

mfg

Bei der im Bild gezeigten Aufgabe handelt es sich um eine Folgeaufgabe. Kann mir jemand erklären, wie man bei Aufgabe c) zu den Antworten gekommen ist? Ich versteh nicht was da gerechnet wurde. Danke im Voraus

Ich rechne gerade eine Abschlussprüfung durch und komme hier auf 42,29° wenn ich es auf 2 Stellen nach dem Komma runde.

Jedoch steht in der Lösung 42,28°

Runde ich falsch oder scheint die Lösung hier falsch zu sein?

Ich habe ein Matheproblem:

ich soll mehrere Ableitungen machen. Damit ich aber mit diesen Ableitungen gut arbeiten kann ist es bei manchen Ableitungen von Vorteil, wenn man sie vereinfacht.

ableiten bekomm ich ganz gut hin aber bei einer bestimmten Sorte Check ich das vereinfachen nicht.

Das hab ich aus der Lösung des Buchs. Aber wie kommt man dazu? Wie geht das? Ich Check nich wie aus ()^2+()^3 plötzlich nur noch ()^2•() werden kann.

kann mir jemand erklären wie man sowas vereinfachen kann?
ich hatte das gleiche Problem vor 1,5 Jahren schonmal und hab es iwann verstanden aber hab vergessen wie’s geht.

danke für eure Hilfe 🙏🏼
LG

Ich habe gerade, während ich für Mathe übe, eine Aufgabe: 2 • (2x - 3) = x • (4 - 2). Bei so einer Gleichung muss man ja zuerst die Klammer auflösen. Das habe ich auf der linken Seite auch hinbekommen. Ich muss ja 2 • 2x und 2 • -3 rechnen, um die Klammer aufzulösen. Aber, was mache ich, wenn ich, wie auf der rechten Seite, x vor der Klammer stehen habe? Wie löse ich dann die Klammer?

Hey,

ich muss für die Uni folgende Aufgabe lösen:

Finden Sie eine Funktion f : R → R, die in 0 differenzierbar und in allen anderen Punkten unstetig ist. Beweisen Sie ihre Behauptung.

Kann mir jemand eine solche Funktion nennen? Ich weiß nicht genau, wie ich auf eine solche schließen kann.

Lg, Paul

x³+2x²+5x+12

x⁴+12x²+6

2x⁴+3x³+15x²+5x+8

x⁵+2x⁴+3x³+x²+7x+9

Wie geht man da am besten vor um die Umkehrfunktion zu bestimmen?

Die Ableitung von sin'(x) ist cos(x) (hier in rot markiert)

cos(x) wird jetzt umgeschrieben zu:

cos²(x) = 1 - sin²(x) | Wurzel

cos(x) = Wurzel(1 - sin²(x))

Jetzt steht hier im Nenner:

Wurzel(1 - sin²(x)) Jetzt müsst man das arcsin x für x einsetzen

"Bei 1 kann man das arcsin x nicht einsetzen"

allerdings bei -sin²(arcsin x)

Fkt und Umkehrfkt fressen sich auf, weshalb sin(arcsin x) = x ergibt

Durch das ² ensteht, dass x². Deshalb steht jetzt im Nenner

Wurzel(1 - x²).

Ich stehe kurz vor meiner mündlichen Prüfung im Abi in Mathe. Ich verstehe wie man ein Integral berechnet und natürlich wie man hochleitet, aber warum muss man dazu hochleiten?

Ich habe eine Frage was der Unterschied zwischen einem Sattelpunkt und einem Wendepunkt in der Mathematik ist. Und voralllem wie sich dich Rechnungen bzw Bedingungen unterscheiden.

Eine Tangente von f(x)=4x*e^-x an der Stelle x0=2 schneidet die x-Achse in P und die y-Achse in Q. welchen Flächeninhalt hat das Dreieck PQR, wenn R der Ursprung ist?

A=1/2*g*h

R ist der Ursprung, heisst R(0|0)

Wie berechne ich aber jetzt die Koordinaten von P und Q? Und was muss ich danach genau machen?

Bitte um Hilfe

Hi,

meine Lehrerin hat bei beiden Aufgaben die selbe Gleichung genommen , obwohl einmal die gesamte Länge der Kathete gesucht ist also y und beim anderen nur ein Teil, kann jemand schauen ob die Lösung stimmt und mir erklären wieso man bei beiden y + eine Zahl genommen hat , obwohl unterschiedliche Längen gesucht sind.

Hallo,

ist die Ableitung von 2^2x
2*2^2,
2*2^2x,
2x*2^2
oder 2x*2^2x

Denn die Ableitung von e^2x ist
2*e^2x.

Auch frage ich mich, ob ich die Potenz einer Funktion in puncto Ableiten als in einer Klammer stehend verstehen darf?
Und wenn ja, nur wenn e im Spiel ist oder auch ohne e?
Dort geschieht nämlich das gleiche wie oben:

f(x)=2(3+4x)^2
f‘(x)=4(3+4x)*4

Der Exponent (hier in der Klammer) wird abgeleitet und mit der Potenz (hier der allgemeinen Ableitung von f‘(x)) multipliziert.

Hallo,

ich verstehe nicht, warum mein Lehrer hier eine Gleichung mit (52-x)² aufstellen muss, anstatt einfach die Katheten zu berechnen. Ich weiß, dass es die Kathete ergibt, die neben x steht, aber warum muss es das Binom auflösen und mit der pq-Formel weiterrechnen? Und anstatt auf den maß neben x zu kommen kommt sie verwunderlicherweise auf den maß x.

kann es mir jemand bitte erklären :

Danke im Voraus 😀

Hallo,

spezifisch geht es mir um den Unterschied zwischen -x^2 und (-x)^2.

so ist z.B. -3^2=-9 und (-3)^2=9.
Warum?

-3^2 ist doch -3*-3
Was ist so anders an (-3)*(-3)?
Wie kommt es zu einem anderen Vorzeichen?

Ich danke für jede Antwort! 🙏

Hallo,

Bei folgendem Integral muss mann zunächst aufleiten um Rechnen zu können.
Wie jedoch wechselt die 2 ihr Vorzeichen?

Man würde ja den Exponenten mit der Potenz multiplizieren, aber 1*2 ist nicht -2.

Ich danke für jede Antwort! 🙏

Hallo,

In der folgenden Übungsaufgabe a) soll ich zeigen, dass f(x) monoton fallend ist.

Hierfür wird abgeleitet:

In der Lösung behauptet man selbstsicher, dass f überall monoton fallend ist. Woher nimmt man jedoch die Sicherheit?
Ist der Fakt, dass die Basis -2e negativ ist ausreichend als Begründung? Kann der Term nicht noch positiv ausfallen?

-3^2 ist ja auch positiv. „Beschützt“ das e einen solchen Ausgang und warum bzw. wie?

Ich danke für jede Antwort 🙏

Also ich mache Abiaufgaben ohne Taschenrechner und anscheinend muss man wissen was cos(0) oder cos(pi) ergibt und dasselbe mit sin. Gibt‘s da irgendeine Eselsbrücke oder muss ich das auswendig lernen? Irgendwas am Einheitskreis vllt?

Ich habe die Quadrik

-2x^2-2xy+y^2+4x+2y-2=0

gegeben. Ich will den Typ der Quadrik bestimmen, indem ich die euklidische Normalform aufstelle und die Gestalt mithilfe der im Skript gegebenen Klassifikation herausfinde. Das allgemeine Vorgehen ist mir bekannt, aber ich komme auf immer umfangreichere Brüche.

Für die Matrixschreibweise x^TAx+2a^Tx+c=0

mit A={{-2,-1},{-1,1}} und a={2,1} und c=-2

bekomme ich bei der Berechnung der Eigenwerte, Eigenvektoren und bei der Nomierung der Eigenvektoren immer umfangreichere Brüche raus. Kann mir jemand helfen bzw. sagen, ob ich Vereinfachungen übersehe?

Hey liebe GuteFrage Community

Wie leitet man die Funktion f(x)=cos x an der Stelle x0=0 , mithilfe des Differenzenquotienten ab?

Ich bin soweit gekommen, dass dort

(Cos h - 1)/h

Steht, aber ich komme beim Grenzwert h gegen 0 nicht weiter. Ich weiß allerdings, dass 0 herauskommen muss. Aber wie beweise ich das?

Vielen Dank im vorraus :)

Hallo,

wie löst man dieses Integral?

Hallo zusammen

Ich stecke seit einiger Zeit bei dieser Analysis fest. Ist dieses Gebiet wirklich so anstrengend, oder ist es nur so, weil ich es im Eigenstudium mache?

Egal:

Ich habe folgende Aufgabe:

Ich soll die exakte Lage der Wendepunkte und Steigung der Wendetagenten ermitteln und eintragen..

Ich löste es so:

• damit ich zur Steigung komme nehme ich die zweite Ableitung doch die ist falsch, sie nehmen 1,5 für y.. ich habe 1/4. Also
• Die Wendepunkte definiere ich mit der 3 Ableitung, weil nur dann x alleine habe, aber das ist falsch. Also komme ich für 1 x 4 hoch für y. Das ist falsch.
• Ich komme auf 4, doch in der Lösung unten sehe ich keine 4.

da ist die Lösung:

Was mache ich falsch??

Danke für Eure Hilfe.

lg E.

Kann man mit einem Taschenrechner die erste und zweite Ableitung einer Funktion direkt berechnen, um sicherzustellen, dass die Ableitungen korrekt sind?

das

Ich brauche bei der 2b Hilfe. Ich habe nur 3 Punkte gefunden, mit denen ich anfangen könnte zu modelieren.

Kann mir jemand alle Punkte nennen und wie ich auf diese komme?

Rekonstruktionen von ganzrationalen Funktionen :

Also das ist eine Mathe Aufgabe aus der Mathearbeit. Da wir übermorgen nachschreiben und ich diese Aufgabe immer noch nicht verstehe, frage ich hier einfach mal nach. Mein Problem ist ich bin mir unsicher bei der Aufgabe b)

sind die Punkte hier (8|0), (4|0) ? Aber was ist mit der 1 ist das auch (1|0)?

Guten Tag,

ich komme bei dieser Matheaufgabe nicht weiter, weil ich sowas bisher noch nicht hatte. Es wäre sehr nett, wenn mir jemand behilflich sein könnte..

Ich habe mir hier schon Hilfen angeschaut, aber meine Funktionsgraphen sehen für mich um einiges komplizierter aus als die anderen.

Es könnte mir aber auch nur so vorkommen….
Danke!🙂

Meine Schätzungen:

D - 1

A - 2

B - 3

C - 4

 Hey Leute, wie kann ich diesen Funktion zeichnen und die Steigung ablesen?

Hallo Leute,

wir beschäftigen uns im Matheunterricht gerade mit der Monotonie, aber da unsere Lehrerin krank war, hat sie uns dazu Aufgaben hochgeladen bei denen ich aber nichts verstehe.. Ich soll die Ausgangsfunktion der Ableitungsfunktion zuordnen und angeben, in welchen Intervallen die Funktion f monoton wachsend bzw. monoton fallend ist. Ich habe aber keine Ahnung wie das funktioniert, weil uns der Unterricht dazu fehlt. Die Aufgabe dazu sieht wie folgt aus: (Aufgabe Nummer 12)

Weiß jemand, wie genau ich das machen soll??

Wenn f(x) zwei höchste Punkte besitzt, sind die beiden Punkte globale Extremen oder gar nichts von denen?

Hi, habe in Kürze eine Mathe Klausur, bei der unter anderem auch die Bestimmung von Extreman drankommen wird. Dabei gilt bei der h.B., dass wenn f"(x)>0, dann Tiefpunkt und wenn f''(x)<0, dann Hochounkt. Was ist jetzt aber, wenn f''(x)=0 ?

Hey, ich habe eine Frage zu den Aufgaben.
Mund zwar habe ich die d ) und e) nicht ganz verstanden

bei der x) setze ich 2 in die f‘(x) Funktion ein oder ?

danke im Voraus !!