Könnte man hier den die Ableitung nicht noch weiter vereinfachen?

Wie man auf die Ableitung kommt ist nachvollziehbar.
Könnte man hier den die Ableitung nicht noch weiter vereinfachen?
Wurzel (1 - sin²(x) ) ist doch das selbe wie Wurzel(cos² (x)) = cos(x) und somit -cos(x) / cos(x) = -1?
3 Antworten
Ich verstehe deinen Gedankengang.
Allerdings musst du beachten, dass
√( 1 – sin²(x) ) ≥ 0
für alle x gilt. Wenn du nun aber
1 – sin²(x) = cos²(x)
anwendest und naiv
√( cos²(x) ) = cos(x)
schreibst, würde es heißen, dass der Nenner auch negative Werte annhemen kann: z.B. für x = π, denn cos(π) = –1.
Würdest du aber x = π in √( 1 – sin²(x) ) einsetzen, erhälst du 1, denn
√( 1 – sin²(π) ) = √( 1 – 0 ) = √1 = 1.
Korrekt wäre, wenn man
√( 1 – sin²(x) ) = | cos(x) |
schreibt. So bleibt der Nenner auch tatsächlich positiv. Allgemein gilt auch die Konvention, dass √( a² ) = | a |.
So ist die Ableitung zwar betraglich weiterhin eins, aber wechselt π-periodisch das Vorzeichen. Wenn du dir die Graphen von f und f' anschaust, sieht du, was ich meine.
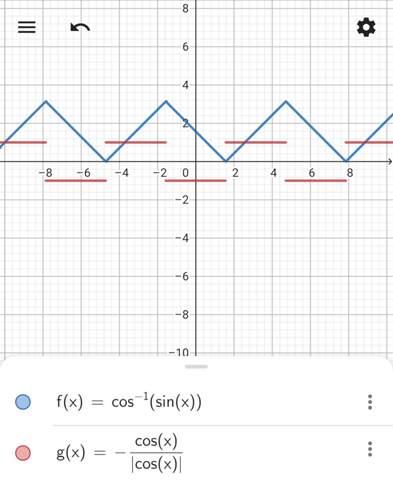
Wäre f' konstant –1, dann könnte arccos(sin(x)) schlecht dieses Zickzack-Muster zeigen. Verstehst du, was ich meine?
Wurzeln sind immer positiv, weswegen du beim "Ausrechnen" der Wurzel an den Betrag denken musst, wenn du eine gerade Potenz mit der Wurzel kürzt.
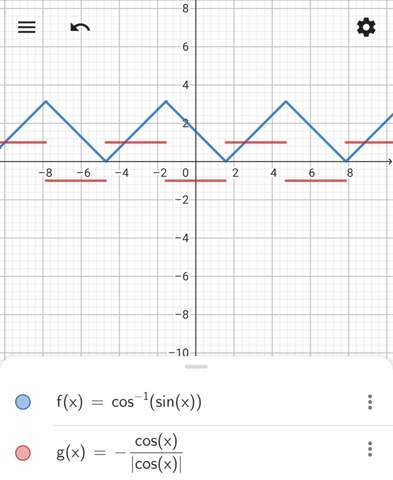
Das mit der Minus 1 ist nicht ganz so sauber
wegen dem Wertebereich, siehe Dir mal die Funktion im Graphenplotter an. Ansonsten wäre
Das gilt nicht allgemein.
Was ist der Wertebereich von arccos?
Diesen Wertebereich mitnehmen und dann überprüfen. Für [-1,1] passt es, wenn Du weitere Wertebereich aber in arccos einbeziehen wollen würdest, würde es falsch werden.
Hallo,
in der Tat. 1-sin²(x) ist gleich cos²(x) und die Wurzel daraus ist cos(x).
cos(x) im Zähler und im Nenner lassen sich zu 1 kürzen, das Minus davor bleibt erhalten, also sollte die Ableitung f'(x)=-1 lauten.
Herzliche Grüße,
Willy
An den Stellen, an denen die Ableitung jeweils das Vorzeichen wechselt, ist die Funktion nicht differenzierbar.
Allerdings mußt Du mit der Wurzel aufpassen. Die Funktion wechselt regelmäßig zwischen Steigung 1 und Steigung -1. Von -pi/2 bis pi/2 gleich -1, von pi/2 bis 3pi/2 ist sie 1 usw.