Liegt der Wendepunkt IMMER genau zwischen Hoch und Tiefpunkt?
Oder kann er auch woanders liegen?
Also z.b HP 4 und 2 und TP 0 und 0, wäre dann die Wendestelle genau be 2 und 1?
Oder kann es sein, dass er etwas weiter links oder rechts liegt?
4 Antworten
Nein. Das muss nicht unbedingt der Fall sein.
Bei einer Funktion ganzrationalen Funktion 3-ten Grades könnte man das folgern, da diese dann punktsymmetrisch bzgl. des Wendepunkts ist. Im Allgemeinen ist das jedoch nicht unbedingt der Fall.
Betrachte beispielsweise die durch...
... gegebene reelle Funktion f. Da hat man (0 | 0) als Tiefpunkt und (4 | 2) als Hochpunkt. Bei x = 2 befindet sich jedoch kein Wendepunkt. Der Wendepunkt der Funktion ist stattdessen (3 | 1,38375).
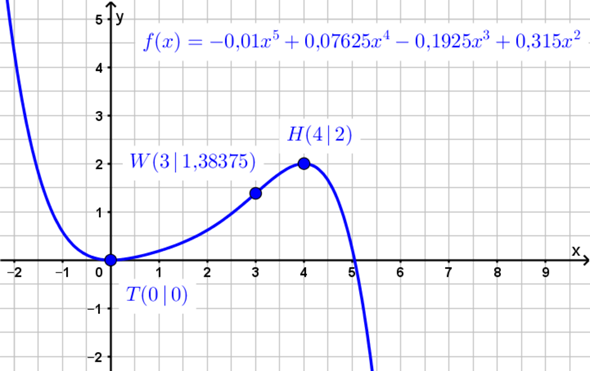
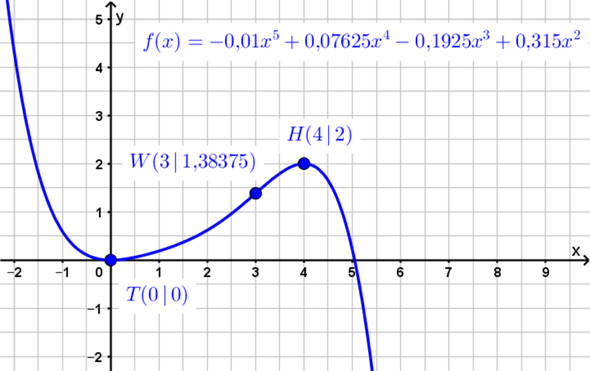
Bei ganzrationalen Funktionen 3.Grades (und nur bei diesen) ist der Wendepunkt Symmetriepunkt und liegt genau zwischen Hoch- und Tiefpunkt.
Muss ja. Ein Hochpunkt ist eine Rechtskrümmung und ein Tiefpunkt ist eine Linkskrümmung. Wo die Krümmung wechselt, ist der Wendepunkt.
Der kann irgendwo dazwischen liegen, muss nicht symmetrisch sein.
Hier
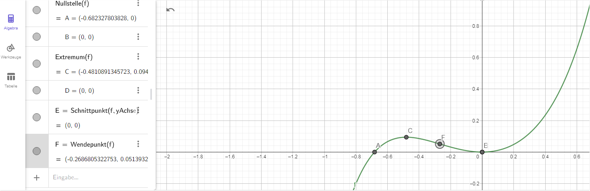
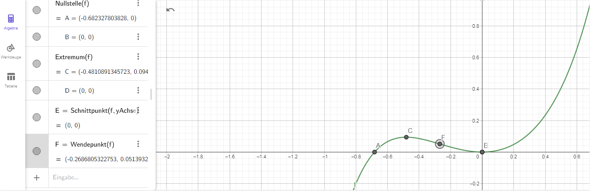
HP bzw TP bei
0 und -0.48
WP bei
-0.26 ( was nicht -0.24 ist , oder ? )
.
Aber Achtung !
Es gibt Aufgabenstellungen ,da wird die Mittigkeit des WP bei Fkt dritten Grades genutzt , um zum Beispiel die x Koordinate des zweiten Extremas zu finden
.
Beispiel TP bei 8 , WP bei 11 , dann muss der HP bei 14 liegen
Wie sieht es aus mit anderen Funktionen, ist da der Wendepunkt aber trotzdem irgendwo zwischen Hoch und Tiefpunkt, also jetzt nicht genau aber er liegt irgendwo dazwischen oder?