Zeigen, dass momentane Änderungsrate abnimmt/legitimer Beweis?
Hallo,
ich hänge grade bei einer Aufgabe fest:
Ein Gerücht verbreitet sich und seine Momentane Änderungsrate (wie viele hören es stündlich) ist durch einen Graph dargestellt.
Wir sollen rechnerisch zeigen, dass die momentane Änderungsrate nach der Zehnten Stunde abnimmt.
Siehe Aufgabe d)

Soweit sogut.
Wir bekommen dafür eine Formel: f(t)=20t^2*e^-0,2t
Mit dieser sollen wir rechnerisch zeigen, dass die momentane Änderungsrate nach der 10ten Stunde abnimmt.
In den Lösungen ist folgender Rechenweg abgebildet:
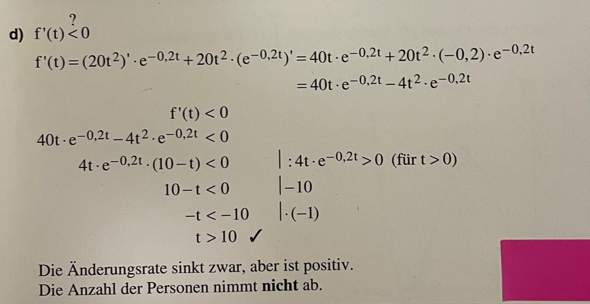
Die ersten drei Zeilen leuchten mir ein, die drei folgenden jedoch kaum.
- Wie kommt man dazu die „40t*e^-0,2t-4t^2*e^-0,2t“ in „4t*e^-0,2t*(10-t)“ zu verwandeln? (Wie wird hier vereinfacht!?)
- Und warum ist das Ergebnis t>10 ein Beweis für das Abnehmen der momentanen Änderungsrate nach t=10?
Ich wäre für eine ausführliche Erklärung sehr dankbar!
Vielen Dank im Voraus! 🙏
2 Antworten
Wie kommt man dazu die „40t*e^-0,2t-4t^2*e^-0,2t“ in „4t*e^-0,2t*(10-t)“ zu verwandeln? (Wie wird hier vereinfacht!?)
40*t*e^(-0,2*t)-4*t^2*e^(-0,2*t)
= 10*4t*e^(-0,2*t)-t*4*t*e^(-0,2*t)
= (10-t)*4t*e^(-0,2*t)
Es wurde also ausgeklammert (Distributivgesetz).
Und warum ist das Ergebnis t>10 ein Beweis für das Abnehmen der momentanen Änderungsrate nach t=10?
Weil es eine Äquivalenz zu f'(t)<0 ist. Also weil aus t>10 folgt, dass f'(t)<0 ist und somit f(t) für t>10 streng monoton fallend ist.
Ja, es geht nur um t>10 (siehe Aufgabe: "[...] nach der 10. Stunde [...]")
f'(10) ist 0 und f'(10+x) <0 für alle x>0. Damit ist die Steigung der Kurve negativ, die Änderungsrate nimmt ab, es kommen pro Zeiteinheit zwar Leute dazu, aber immer weniger
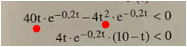
man hat 4t*e^(-0.2t) ausgeklammert . Das gepunktete bleibt ( die 10 in 40 und ein t in t² )
Ausgangspunkt ist die Frage ::::::::::::::: f'(t) < 0 ?
Antwort nach Rechnung : Dann und nur dann ,wenn t > 10
Was hier nicht der Fall ist
.
Den letzten Satz kann ich nicht wirklich nachvollziehen . Tatsache ist ,dass bei t = 10 die Änderungsrate genau Null ist . Wie man im Graph auch erkennen kann .
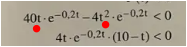
wobei mit der letzte Satz im Geposteten nicht wirklich einleuchten will . Ist damit der Verlauf nach t > 10 gemeint ?
f'(10) ist ja Null .