Mal angenommen ich habe einen Außendurchmesser von 3,5m. Wie rechne ich dann den Umfang und die Fläche aus? Bzw. wie gehen die Formeln?

Wie löse ich diese Aufgabe?

Danke :)

ich mache gerade eine Konstruktion Aufgabe und da steht c= |AB| =4,8 cm

sitze seit 40min dran und verstehe nichts

danke im voraus

es sind nur q und die höhe gegeben

danke im voraus

Ich wollte meine Körpergröße messen und habe mich grade an eine Wand gestellt wie üblich wenn man sich misst und habe eine Markierung gemacht und laut Zollstock soll ich 174/175 sein obwohl das nicht korrekt ist ?

Ist eine Zollstock Messung genau oder verschiebt sich das um cm ? Weil meine Mutter 165 ist und der Zollstock anzeigt , dass sie mit meinen ca.178 so groß ist , dass ihr Kopf in der gleichen Höhe wie meine Augen ist aber das stimmt nicht?

Hallo Mathefreunde,

ich schreibe diesen Freitag eine Klassenarbeit über die Strahlensätze und verstehe so gut wie nichts. Also wollte ich mal fragen ob mir irgendein Mathefreund erklären kann wie ich x und y berechne.

Moin!

Ich muss in Mathe als Hausaufgabe eine Tabelle ausfüllen (linke Spalte: „Der Graph der Funktion f…“, mittlere Spalte: „Skizze des Graphen“ und rechte Spalte: „Bedingungen“) komme aber bei dem Ausschnitt (Siehe Foto) einfach nicht weiter. Den Anfang der Tabelle habe ich schon bearbeitet, aber den Rest hier verstehe ich nicht. Unser Lehrer ist das mit uns noch nie durchgegangen.

Könntet ihr mir eventuell dabei helfen? Zumindest bei der linken und rechten Spalte?

LG und Danke!

Kann mir das einer anhand dieser Aufgabe erklären? Ich muss noch mehr solche Aufgaben machen. Ich brauche für den Anfang nur mal ein Beispiel zum Verständnis. Die anderen Aufgaben kriege ich dann damit denke ich auch alleine hin.

A ( 3 | 2 | 0 )

B ( -1 | 4 | 0 )

P ( 1 | 3 | 0 )

Wie finde ich jetzt heraus, ob der Punkt P auf der Geraden liegt, die durch A und B geht?

Kann mir jemand hier helfen.

Wie soll ich das rote Dreieck berechnen.

Ich habe keine klare Längen.

Danke im Voraus

LG

Wie kann man den Abstand in Lichtjahren zwischen zwei Sternen berechnen? Zum Beispiel den Abstand zwischen Alpha Centauri und 18 Scorpii. Geht das mithilfe der Deklination und Rektazension? Gibt es im Internet evtl. einen Rechner dazu?

Überprüfe folgende Aussage?

Das Verhältnis von Diagonalenlänge und Seitenlänge für Quadrate ist stets

gleich √2.

Ist diese Aussage korrekt? Wie kann man das überprüfen?

a = 12 m; b = 6 m; c = 5 m und d = 9 m. Wie hoch ist das Walmdach?

Wie berechne ich das genau?

Kann ein Trapez ein Paralelogramm sein und kamm ein Parallelogramm ein Trapez sein??

Mit Beründung bitte

Danke im Voraus

LG

Guten Tag,

ich habe derzeit im Mathe-Unterricht Geometrie und wir benutzen den Zirkel. Da ich auf dem Tablet mitschreibe brauche ich noch die passende App dafür kennt zufällig jemand eine App dafür? Für Android (Samsung)

Gegeben ist das Quadrat ABCD mit dem Dreieck AEF

Berechne den Winkel vom Fragezeichen

Hallo zusammen!

Es wäre wirklich nett, wenn mir jemand bei diese Aufgabe helfen kann. Ich habe die Orientierung drüber verloren weil ich seit einer Weile nachdenke, wie es aussehen könnte.

Ich wäre euch echt dankbar, wenn ihr helfen könntet

Wie berechne ich bei einem Diagramm den Weg wenn ich keine Funktion gegeben habe, sondern nur den Graphen? (Geschwindigkeit und Zeit sind jedoch angegeben)

Sollte es nicht v*t =s sein?

Und zwar ist er geschwungen (sprich negativ gekrümmt und dann positiv gekrümmt)

Siehe Bild:

Vielen Dank.

Bei Aufgabe 8 komme ich zum verzweifeln,da mein lehrer uns nie beibrachte,wie man die Höhne ausrechnen kann. Könnte jemand es mir noch Kindgerecht vllt sogar anhand einer Aufgabe bzw. Beispiels erklären. Danke im voraus

Moin. Ich kann mir beinahe jedes Viertel Jahr ein neues Geodreieck kaufen, da dauernd die Zahlen, bzw die Striche abgehen. Wisst ihr was man da machen kann?

Es dauernd an zu heben ist zu umständlich...😅

Hallo liebe Leute, es geht um die Frage A1 ich verstehe nicht was er meint mit die resultierende muss verschwinden? Also könnte mir da bitt jemand kurz den Sachverhalt erklären und die Lösung?

Ich habe bis hier geschafft und weiß nicht mehr weiter kann irgendjemand mir helfen.

Hallo allerseits, das Volumen berechnet man ja mit der Formel V=G×h und die Fläche vom Trapez berechnet man ja mit A=c+d zweitel ÷ h. Aber irgendwie weiß ich nicht recht,wie ich das ganze jetzt rechnen soll

Hi Leute,

ich beschäftigte mich in der Freizeit mit solchen Rätseln, aber ich komme einfach nicht weiter.

Aufgabe 1. Winkelhebel: Muss man da das Hebelgesetz anwenden F•S = F•S

Aufgabe 2. Schalthebel: Was ist das? Bei dieser Aufgabe verstehe ich einiges nicht! Wie wird das betätigt? Ich würde mich freuen, wenn man bei jeder Antwort eine knappe Erklärung rasch hinlegt😊

Ihr müsst mir es auch nicht erklären, aber wenigstens die Antwort geben, dementsprechend könnte ich es eigenständig herausfinden und verstehen👍

Vielen Danke👌👌⚡️

Hallo und zwar soll ich davon den Flächeninhalt berechnen und stehe jedoch gerade voll auf dem Schlauch. Also eine Fläche ist 18. Das heißt die Links oben. Habe ich berechnet indem ich 6/2*6 gerechnet habe. Stimmt das soweit und wie kommt ich auf das andere Dreieck?

Hallo liebe Community könnt ihr mir bitte bei einer Mathematik Aufgabe helfen!

Das mit dem Dreieck. Also Alpha=52° W Alpha=6,5cm und a=hc.

Hoffe ihr könnt mir helfen.

Hallo,

Wir sollen als Hausaufgabe den Flächeninhalt des hier gezeichneten Körpers berechnen.

Was für eine Formel muss ich da nehmen?

Ich hab schon bei mir im Tabellenbuch geschaut, aber nichts richtiges gefunden.

Die Fläche mit dem A in der Mitte ist gemeint.

Danke!

Wir haben in Physik folgende Aufgabe erhalten:

Aus einem homogenen kreisförmigen Blech mit dem Radius R wurde ein Kreis mit dem Radius R/3 ausgeschnitten (siehe Abb.). Bestimmen Sie die Lage des Schwerpunkts relativ zum Zentrum U des Bleches, wenn UZ = R/2, wobei Z das Zentrum des Kreises ist.

Als Lösung wird (-R/16) angegeben.

Ich komme aber auf (-R/18).

Mit folgender Rechnung:

Sieht jemand einen Denkfehler oder woran könnte das sonst noch liegen :(

Wie gehe ich da voran?

Wie siehtn der aus ? Also von die Grundplatte wie gezeichnet ist auf einem I Träger befestig ( mit Klemmen ). Wie sieht denn der I-Träger dahinter aus ? Ich bin komplett lost mit der Ansicht. Kann jemand das schnell skizzieren ?

Guten Abend,

ich beschäftige mich gerne mit solche technische physikalische Rätsel aus dem Netz, aber bei der bin ich echt am frustrieren. Ich verstehe es einfach nicht.

Dreht sich der Schwungrad um seine eigene Achse oder schwingt er richtung Pfeil? Soll der Schwungrad den Kolben zum bewegen bringen? Welche Strecke soll man errechnen?

Die grundsätzliche Frage ist, wie lange die Strecke ist?

Es wäre ehrenvoll wenn jemand nur wenigstens diese Frage beantwortet, vielleicht ergibt sich der Rest.

Vielen Dankéèė

Wie kann ich ich die höhne h eines Prismas berechnen,wenn diese nicht angegeben ist? Danke im voraus

Nehmen wir an, wir haben ein Dreieck, wir wissen die grundseite und eine Seite. Aber man muss die andere berechnen, OHNE den Satz des Pythagoras, da es nicht rechtwinklig ist.

Wie stellt man das an? Im Internet finde ich nur, wie man das mit einem rechtwinkligen Dreieck macht.

Das Viereck ABCD sei ein Parallelogramm, bei dem der Abstand der parallelen Geraden AB und CD gleich 6 ist. E und F seien die Mittelpunkte der Seiten BC und CD. Die Gerade DE schneide die Strecke BF im Punkt P und die Gerade AB im Punkt Q.

a) Zeigen Sie, dass |AQ| = 2 |AB| gilt.

b) Zeigen Sie, dass P auf der Geraden AC liegt und bestimmen Sie die Länge des Abstands von P zur Geraden AB.

Hilfe mit Lösungsweg wäre nett.

Hey

wir sollen sagen, ob diese Begründung

a)schlüssig und richtig oder

b)nicht schlüssig und somit falsch ist.

ich finde, es macht zwar Sinn, aber da steht ja “Legt man nun ALLE Winkel nebeneinander,…”, das ist finde ich nicht ganz eindeutig, weil man so ja auch noch die Winkel Alpha und Beta von der Strecke AB mitzählen könnte…

was meint ihr? A oder B?

Ich muss bei einer Mathearbeit einen Behälter für 4 Tischtennisbälle aus papier basteln. Einen quaderförmig und einen NICHT prismenförmig. Wenn ich allerdings nicht-prismenförmige körper google kommen nur prismeförmige Körper oder ergebenisse mit denen ich nix anfangen kann. Kann mir jemand bitte einfach sagen z.b. "Ein Zylinder ist nicht prismenförmig aus dem Grund . . ." (Ich weiss nicht ob ein Zylinder prismenförmig ist oder nicht). Danke für die Hilfe.

Ich muss nur den Umfang bestimmen

Ist es das Volumen oder der Oberflächeninhalt oder ist es was ganz anderes?

Für mehr Kontext:

Es geht um eine quadratische Pyramide.

In einem kartesischen Koordinatensystem werden die Pyramiden ABCDSk mit A(000), B(200), C(220), D(020) und Sk (11k) mit k>1, element R betrachtet.

Die gemeinsame Grundfläche ABCD dieser Pyramiden ist quadratisch.

Berechnen Sie für k=4 den Inhalt der Mantelfläche der geraden Pyramide ABCDS4

Hallo, ich schreibe morgen einen Test und komme bei folgender Übungsaufgabe nicht weiter: Ein Kreisverkehr hat eine Mittelinsel mit dem Durchmesser 20m. Die Fahrbahn um die Mittelinselherum hat eine Breite von 3,5m. Die Fahrbahn soll neu geteert werden. Welche Fläche muss geteert werden?

Bitte mit Rechnung und danke im voraus

c. Auf der Fahrt von A nach B hatte das Schiff im Punkt D den kürzesten Abstand zu C. Berechne, wie weit das Schiff in D vom Leuchtturm C entfernt war!

ich hab 9,72

Ich befinde mich zurzeit beim Thema: Sinus, Kosinus und Tangens. Ich habe verstanden, was diese bedeuten, wie sie anzuwenden sind, was die Sinussätze bzw. Kosinussätze sind. Allerdings tue ich mich momentan etwas schwer mit dem Einheitskreis. Nicht wegen des Ablesens an sich, sondern wie man z.B. zu einem gegebenen sin(234°) = -0.809 (gerundet) den zweiten Winkel findet, für den ebenfalls sin(a) = -0.809 (gerundet) ergibt.

Zu dem Beispiel an dem ich momentan feststecke war folgendes:

Der Taschenrechner liefert für sin(300) folgenden Sinuswert: Gesucht ist nach der Aufgabenstellung ein zweiter Winkel, der ebenfalls die gleiche Lösung wie für sin(300°) liefert. Alle meine Versuche auf diesen Wert zu kommen schlugen fehl (obwohl ich weiß, dass es wohl 240° sein müssen, aber ich würde es gerne rechnerisch ermitteln), und ich komme wirklich nicht mehr weiter bzw. bin etwas frustriert.

Ich habe hier dabei folgenden Ansatz versucht:

Ich weiß, dass sin(300°) auf dem Einheitskreis im vierten Quadranten liegt. Folglich muss ich doch irgendwie rechnerisch zu dem Winkel gelangen können, für den ebenfalls -1/2*Wurzel3 rauskommt. Ich habe dabei gedacht, dass  die Lösung sein könnte. Allerdings macht das ja keinen Sinn, da ich einen Winkel von 480° erhalte. Das ist zwar auch eine mögliche Lösung, allerdings soll der zweite Winkel im Intervall von 0° bis 360° liegen. Ich verstehe nicht, wie ich hier rechnerisch auf 240° kommen soll.

Vermutlich ist das evtl. wieder sehr trivial und ich habe mich vielleicht hineingesteigert in die Frustration, sodass ich was offensichtliches nicht bemerken könnte. Aber mir fällt nichts mehr ein, wie ich hier jetzt auf diesen zweiten Winkel kommen soll.

Ich hoffe, mir können hier einige Experten helfen.

Ist jede Raute auch ein Drachenviereck? und warum?

Vielen Dank!

Hallo gemeinsam,

und zwar habe ich eine kurze Frage zum vektoriellen Flächeninhalts eines Dreiecks. Die Formel ist mir klar, ich weiß was was ist. Aber die Herleitung des ganzen ist mir etwas unübersichtlich. Ich habe kein Video gefunden, das mir es etwas verständlich erklären könnte. Dafür habe ich aber eine PDF- Datei gefunden, die das ganze anschaulich gemacht hat. Die ersten Schritte habe ich soweit verstanden, aber ab dem Punkt mit dem sin und con Umstellung und das Verschwinden der 1 unter der Wurzel ist mir etwas unklar. Allgemein ab dieser Umstellung.

https://c.wgr.de/f/verlage/westermanngruppe-at/dimensionen-mathematik/_dim6/materialien/12_AnalytischeGeometrie/02_Flaecheninhaltsberechnung/12_02_vektorielle_flaecheninhaltsformel_AB.pdf

Könnte mir jemand dabei helfen und es mir eventuell etwas einfach, verständlich erklären?

Ich danke Euch im Vorraus!

Hallo, Nr. 1 have ich geschafft und ich denke es sollte auch richtig sein aber nun habe ich Schwierigkeiten mit der zweiten Aufgabe. Könnte mir jemand behilflich sein und mir das gut erklären da es Übungsaufgaben für einen Test sind, den wir bald schreiben. Danke im Voraus!

Hi,

wie man ein normales Parallelogramm berechnet, ist mir schon klar, aber dieses Parallelogramm ist iwie anders.

Wie berechne ich den Flächeninhalt?

Wie kann ich herausfinden was a ist?

Ich muss den radius eines Halbkreises und eines Viertelkreises Berechnen. Der flächeninhalt beider Figuren ist A=10hoch2. Wie geht das?

Ich bleibe bei dieser Aufgabenfrage hängen, weil mir nichts sinnvolles einfällt wie man einen Rechteck zeichnen kann nur mit 3 Strichen. Habt ihr welche Ideen wie es möglich wäre?

Hallo,

im Thaleskreis gibt es ein Dreieck mit maximalem Flächeninhalt... kann mir jemand das begründen und den zugehörigen Wert dafür geben?

danke schonmal im Voraus

Für welches Verhältnis von Breite zu Höhe eines schmalen Tafeleisberges wird die meiste Energie durch das Umkippen freigesetzt. Nimm dabei an, dass L > H ist. Könnt ihr mir dabei helfen oder mir einen Ansatz geben?

Hey, ich programmiere gerade an einem 3d Viewport und bin auf ein Problem gestoßen, als ich versucht habe Objekt zu rotieren. Beim Rotieren(oder zumindest so wie ich das implementiert habe) wird erst über die x, die y und dann die z-Achse gedreht, das Problem dabei ist, dass dann so zu sagen die Rotation über die x-Achse bei y und z noch mal mitgedreht wird und so für eine Rotation an der x Ache nicht zu einer über die globale x-Achse, sondern eher über eine lokale Achse des Objekts führt. Tatsächlich ist das auch das, was ich am Ende gern hätte, aber halt nicht nur an einer Achse. Was ich also suche, ist eine Möglichkeit einen Punkt im dreidimensionalen so zu rotieren, dass er zum Rotieren entweder nur lokale Achsen benutzt oder nur globale aber halt nicht irgendeine Mischung aus beidem. Hier ist noch der code den ich bis jetzt geschrieben habe:

point.yz = vec2(point.y * cos(rotation.x) - point.z * sin(rotation.x), point.y * sin(rotation.x) + point.z * cos(rotation.x));

point.xz = vec2(point.x * cos(rotation.y) - point.z * sin(rotation.y), point.x * sin(rotation.y) + point.z * cos(rotation.y));

point.xy = vec2(point.x * cos(rotation.z) - point.y * sin(rotation.z), point.x * sin(rotation.z) + point.y * cos(rotation.z));

Weil dann ist ja das Ergebnis immer unterschiedlich

Alle Klassen meines Jahrgangs haben PDFs zugeschickt bekommen, da wir nach den Ferien einen Vergleichstest in Mathe schreiben. Auf einer der Seiten steht folgendes:

Allerdings bin ich hier stutzig geworden, denn ich dachte Sinus und Kosinus sind immer das Verhältnis zwischen einer Schenkelseite und der Hypothenuse. Hier ist der Sinus aber plötzlich als Ankathete durch Gegenkathete definiert. (ich bin der Meinung es ist Gegenkathete durch Hypotenuse)

Also habe ich das all die Jahre falsch gemacht oder ist dieses Dokument falsch?

Bitte helft mir ich bin verwirrt 😂.

Danke im voraus. Lg Torty

Damals im Mathematikunterricht fiel mir das Thema Parabeln nicht leicht, da es zu theoretisch war. Kann man das irgendwie im Alltag oder Berufsleben irgendwo anwenden. Das einzige Beispiel, was wir im Unterricht gerechnet haben, wo man es irgendwie praktisch anwenden konnte, war bei der Berechnung an den Bögen von Brücken.

Hallo,

Ich hoffe man versteht, was ich mit meiner Frage meine. Wenn ich eine Funktion betrachte und davon die Stammfunktion bilde und dabei C = 0 setze. Was bedeutet diese Funktion dann geometrisch interpretiert. Also, wenn ich z.B x = 3 einsetzte, erhalte ich dann dann die Fläche meiner Ausgangsfunktion mit der x-Achse im Intervall von 0 bis 3 ?

Wenn ich C = -3 setze und dann x = 3 einsetzte, erhalte ich dann die Fläche meiner Ausgangsfunktion mit der x-Achse im Intervall -3 bis 3 ? Oder liege ich da falsch? Ich kann mir irgendwie nicht so ganz vorstellen, was die Stammfunktion geometrisch angibt. Oder gibt es diese geometrische Interpretation nur für das bestimmte Integral.

Würde mich über eine Antwort freuen.

Jonas ( - :

Was ist der Unterschied zwischen Arcussinus und Sinus? Wird Arcussinus oder Sinus für rechtwinklige Dreiecke benutzt? Oder ist das egal welches Dreieck? Wie heisst die Gleichung? Und wie wird Cotangens ausgerechnet?

Wenn ich einen Punkt



habe, von diesem Punkt aus eine Strecke zum Ursprung konstruiere und dann den Winkel zur x-Achse berechnen will (im Bogenmaß), wie mache ich das?

Hallo, ich verstehe dieses Thema überhaupt nicht . Kennt sich jemand damit aus?

Bitte helft mir

Hey mache bald ne mathe fachexkursion muss dort einen fachlichen beitrag leisten und hab vor über orientierbare, bzw. nicht orientierbare flächen zu machen speziell am beispiel Möbiusband. weiß aber nicht wie ich sowas kreativ gestalten könnte und am besten die schüler mit einbeziehen kann. weiß auch nicht so richtig welche informationen alles so relevant sind um ein vortrag darüber zu machen

brauch hilfe muss meine idee morgen vorstellen

Die Sehne eines Betonkegels hat einen Winkel von 65° zur Grundfläche. Der Umfang des Kegels beträgt 3,78 m. Welche Höhe hat er? Runde auf Zentimeter.

tan (65°) * 0,6m = 1,3m in der website wird das Ergebnis als falsch bewertet warum?

Viele Grüße

Hallo zusammen, Erstmal Entschuldigung für meine Grausame zeichnung.

Meine Frage ist : Ich bin grad dabei einen Konus zu berechnen der Konus soll 7grad haben, Der 1 eingangsdurchmesser steht fest er soll 31 mm im durchmesser haben.

Nun ist die Frage wie errechnet sich der Durchmesser 2 Und die gesamte länge des Konuses.

Vielen Dank schonmal für euere ganzen Antworten

Ich stehe hier vor diesem Mathe Problem, und kann es nicht lösen, ich muss aber bald einen Vortrag darüber halten

Wäre super, wenn mir jemand dabei helfen könnte:)

Hi Leute komme einfach nicht weiter, wäre super lieb wenn ihr mir helfen könntet. Habe gefühlt schon alles probiert. Lg

Hallo,

ich hab die letzten 2 Jahre nicht aufgepasst und jetzt hab ich übermorgen Matheabitur. Ich muss nur einen Punkt schaffen also gebt mal bitte Tips wie ich das am besten anstelle. Dran kommen tut Analysis, Stochastik und Geometrie. Ich kann von den drei themen alle gleich schlecht bzw gut.

Danke

Wie berechne ich das?

Hi, und zwar muss ich die Aufgabe b) machen. Aber wie mache ich das am einfachsten? Ich weiß, dass das Skalarprodukt=0 sein muss. Aber geht das nur durch ausprobieren? Kann ich mir eigentlich nicht vorstellen

Hi liebe Leute und zwar bin ich nicht so gut in Geometrie deshalb kann ich kann ich nicht so ganz nach vollziehen woher der Wert 2/3 kommt ( ich habe Screenshots hinter lassen ). Wäre echt super wenn mir dies einer ausführlich erklären würde wie 2/3 zustande kommen.

lg vielen Dank im Voraus

Hey Leute ich brauche Hilfe bei der Herleitung der Höhe eines Tetraeders. und zwar wie ich komme ich auf die 2/3 (Siehe Screenshots) ich verstehe einfach nicht wie man auf 2/3 kommt. Kann mir jemand weiter helfen?

Hallo ist die Winkelhalbierende im 2. und 4. Quadranten von links unten nach rechts oben, oder von rechts unten nach links oben?

Vielen Dank schon mal

Ich brauche Hilfe bei dieser Aufgabe. Ich weiß wirklich nicht, was ich machen soll.

Ich denke, ich muss die Parametergleichungen in die y=mx+n Form bringen, aber ich weiß nicht, wie ich das mit drei koordinaten mache. Der Schnittwinkel wird ja durch den Tangens der Beträge der Anstiege berechnet. Ich komme aber irgendwie nicht auf gescheite Gleichungen

Mein Lehrer erklärt das zu schlecht für mich... bin da leider nicht der einzige, der es nicht versteht und wenn ich mich melde ruft er mich nur selten auf. :/

Wäre schön, wenn mir das mal jemand erklärt wie man vorgeht bei den einzelnen Aufgaben ganz kurz reicht schon hauptsache ich habe das Prinzip raus:

Das Thema ist Trigonometrie.

ABC ist ein Gleichschenkliges Dreieck mit der Basis AB. Berechne aus den gegebenen Größen die übrigen, sowie die Höhe zur Basis und den Flächeninhalt.

a) c=25 ;

Der Winkel Gamma beträgt 72°

Ich verstehe die allgemeine Aufgabe nicht. Kann mir einer das bitte lösen und erklären?

Hallo ich habe den Mittelpunkt M eines Kreises gegeben und dessen Radius r davon. Ich habe auch noch zwei Vektoren (v1 & v2) gegeben die von zwei zufälligen Punkten auf dem Kreis M in eine Umlaufrichtung zeigen. (Siehe Bild)

Ich brauche jetzt eine Mathematische Lösung wie ich ausrechnen könnte ob die beiden Vektoren in die Selbe umlauf Richtung zeigen oder nicht.

Ich muss das später Programmieren und deswegen kann ich das nicht einfach mit Logischem Menschenverstand Lösen.

Danke für eure Zeit

Ich verstehe das Konstruktionsverfahren bei Vierecken nicht. Also es ist eine gewisse Länge von einigen Seiten angegeben und von diesen Informationen muss ich dann ein Viereck konstruieren. Wie geht das?

Hey, ich muss diese aufgabe hier lösen. Ich habe auch schon eines Ansatz wie ich das löse(den sinussatz nutzen) aber ich verstehe nicht wie ich auf den Winkel vom leuchtturm komme. Dort ist ja schon ein ''äußerer Winkel" mit 70 Grad aber wie komme ich auf den innenwinkel.

Kann mir das jemand erklären?:)

Ich starte ein großes Bauprojekt in überleben. Hierfür habe ich vor eine 60x60m großes Loch zu graben, das aber so rund wie möglich sein soll.

So habe ich es gemacht. Das ganze ist frei entstanden und nach keinem bestimmtem Prinzip

Das ist ein Virtel des „Kreises“

Ich weiß leider nicht wie ich das rund genug hin bekomme.

Vielleicht kann mir ja einer helfen der sich mit so etwas auskennt.

LG Michiboy

Weiß jemand die Antwort darauf..

Hier ein Beispiel aus dem Buch :

Ich kann die zentrische Streckung nutzen bzw. anwenden aber ich weiß nicht wie ich vorgehen soll wenn die Aufgabe heißt: finde k bzw das streckzentrum raus?

ich bedanke mich für die Erklärungen

lg

Gegeben sei ein Parallelogramm ABCD (Standardnotation).

Es seien M(b) der Mittelpunkt von b und M(c) der Mittelpunkt von c.

Beweisen Sie :

̅̅̅̅̅̅̅̅̅ ̅̅Die Strecken AM(b) und AM(c) teilen die Diagonale BD

in drei gleichlange Teile.

Hallo , kann mir vielleicht jemand hierbei helfen denn es ist eine Hausaufgabe aber ich verstehe sie leider überhaupt nicht . Danke schonmal

Hallo, ich möchte eine Fläche mit 80 Löcher berechnen.

Die Größe der Fläche suche ich.

Ein Loch hat einen Durchmesser mit 6,5 cm

Dieses Loch ist an 4 Seiten 1 cm breit. So das ein Quadrat entsteht.

Außerdem muss in der Mitte der Fläche ein quadratisches Loch mit den Maßen 13cmx13cm sein. Die Fläche muss 4:3 sein.

Wie berechnen ich das?

Danke schon mal im voraus.

wie kann es zur hölle sein das Deutschland zb 357000km2 groß sein soll wenn 1km2 1000mx1000m sind. Da müsste Deutschland ja laut der Angabe 357000km lang und breit sein. Was ja wohl schlecht möglich ist wenn der gesamte Erdumfang 40000km sind. Ich finde dazu nirgends eine Erklärung. Genauso wie die USA mit ihren knapp 10mio km2. Wie zur Hölle soll das gehen?

Hallo weiß jmd wie ich diese Aufgabe lösen soll?

"JOY möchte in ein Gefäß 1l Wasser abfüllen. Das Gefäß hat die Form eines Zylinders und einen Innendurchmesser von 12cm. Berechne die Füllhöhe. Runde auf Zentimeter"

Wie soll ich diese Aufgaben lösen, was soll ich wie berechnen?

Bzw. was für ein Teleskop braucht man da und wie viel kostet das?

Ich habe mir dieses Video auf YouTube angesehen:

https://youtu.be/0t4aKJuKP0Q

Einen 4D-Block Simulator. Er stellt die vierte Dimension als Raum dar. Dabei driften Aspekte des Würfels in die vierte Raumdimension ab und werden unsichtbar. Dabei wird die 2D-Welt-Analogie zur Erklärung verwendet, oder zumindest zur Annäherung an ein Verständnis der/einer vierten Raumdimension. In dieser sähe ein 2-dimensionales Wesen nur den Querschnitt eines Balles, der sich durch die Dimensionsebene des 2-dimensionalen Feldes bewegt.

Mehrere Fragen diesbezüglich:

1. Die Annahmen beruhen doch auf der Vorstellung von der Existenz von n-dimensionalen Objekten. Gibt es denn überhaupt n-dimensionale Objekte für 0 < n ≠ 3, n∈ℕ?

2. Sähe ein 2-dimensionales Subjekt wirklich den Querschnitt eines Balles (sprich einen Kreis), oder nicht nur eine Linie, da es ja nicht von außen auf das Feld bzw. auf die Ebene sehen kann?

3. Falls (2.) insofern wahrheitsgemäß beantwortet werden kann, dass das 2-dimensionale Subjekt nur 1-dimensional sehen kann, ließe sich induktiv schließen, dass n-dimensionale Subjekte stets nur (n-1)-dimensional sehen können, wobei n der Existenzdimension des beobachtenden Subjektes entspricht?

4. Falls (3.) wahrheitsgemäß als wahr beantwortet werden kann, wieso sehen 3-dimensionale Subjekte dann (scheinbar) 3-dimensional? Liegt die Lösung hier vielleicht sogar wirklich im Schlüsselwort "scheinbar"?

Hey

Muss für Mathe einen 75° Winkel konstruieren.(Also ohne Lineal)Weiß jemand wie das geht?

Wie formt man die Formel V=[(pi*h)/3]*(r1^2 + r1r2 + r2^2) so um dass r1 bzw r2 = .... steht?

Könnte mir jemand bei 14 sagen, wie man ihn ausrechnet?

Damit ich es verstehe, dabke

der nachgesagt wird, sie wäre ein Energiegenerator, ein Sternentor oder was auch immer. Bei diesen Aussagen fällt gelegentlich der Begriff Brennpunkt und es wird ebenfalls behauptet, die große Grabkammer läge in diesem Brennpunkt.

--------------------------------------------------------------------------------------

Ich frage nach dem Brennpunkt.

Abhandlungen über Energie ob ja oder nein und Sternentore und Aliens sind fehl am Platz.

Hi,

kann mir wer bei der Aufgabe helfen?

Eine Moschee besitzt eine vergoldete Kuppel, die ungefähr als Halbkugel mit einem Durchmesser von d=23m angesehen werden kann.

Nimm an, die Kuppel ist mit einer Blattgoldschicht von 0,0001cm Dicke vergoldet. Wie viel kg wiegt die Goldschicht, wenn 1cm^3 Gold 19,3g wiegt?

Mein Ansatz:

Ich habe Schon das Volumen der Kuppel ausgerechnet:

r= 11,5m

O= 4*pi*11,5^2/ 2 = 830,95 (m^2)

Kann mir jemand bei dieser Aufgabe die Erklärung machen wie man die Gleichungen ausstellt und wie man sie rechnet

Hallo,

wie kann ich hier das Volumen eines Quaders herausbekommen? (Mit Formel)

Gegebene Werte:

a = 0,5 mm

b = 1,2 cm

Ao (Oberflächeninhalt) = 49,5 mm^2

Vielen Dank!

Hey ich komme mit der 6 a) nicht weiter

Tangente bestimmten habe ich noch hingekriegt, aber warum wird die fläche der tangente und die fläche der geraden addiert? (siehe Lösungen)

oder steht es schon in der aufgabe und ich habs einfach nicht verstanden?

Jedenfalls Danke im Voraus!

Hallo, ich bin momentan in der 9. Klasse eines bayerischen Gymnasiums und bräuchte Hilfe bei einer Matheaufgabe, welche ich unten als Bild eingefügt habe. Es geht darum, dass ich nicht weiß, wie genau ich das Schrägbild eines Prismas zeichnen soll.

Ich wäre froh über eine gute Erklärung oder eine Lösung, vielen Dank im Voraus :)

Kann jemand weiter helfen?

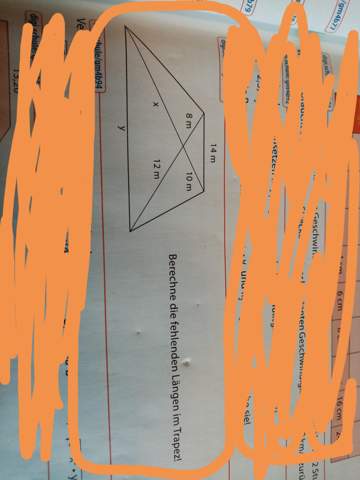
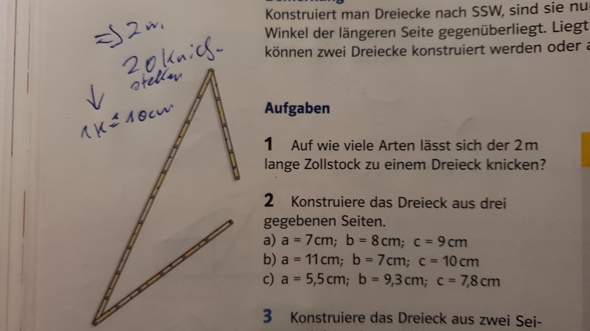
Momentan stehe ich vor einer Aufgabe, die ich nicht wirklich lösen kann. Ich habe bereits dazu eigene Überlegungen gehabt (siehe unten), aber komme dennoch nicht auf eine entsprechende Lösung. In der Aufgabe wird die Frage gestellt, auf wie viele Arten der 2m lange Zollstock (abgebildet im Buch, Bild hier angefügt) zu einem Dreieck geknickt werden kann. Mir ist die Dreiecksungleichung bekannt und an dieser orientierte ich mich auch hauptsächlich.

Nun zu meinen Überlegungen:

Der Zollstock ist 2m lang, und hat 20 Knickstellen, von denen also eine Knickstelle genau 10cm lang sein muss. Ich habe orientierend an der Dreiecksungleichung festgestellt, dass die Schranke der beiden Seiten immer so zwischen 0,5m und 1m liegen muss. Ebenso darf die Summe der beiden Seiten natürlich auch nicht größer sein als der Umfang des Dreiecks, sondern eben nur größer als die dritte Seite (hier c).

Ich habe mir erst überlegt alle Kombinationen durchzugehen, und dabei Aufgaben an der Grenze notiert wie:

0,6m + 1,3m > 0,9m
0,7m + 1,2m > 0,9m
0,8m + 1,1m > 0,9m
0,9m + 1,0m > 0,9m

Zähle ich dann jeweils durch für den zweiten Summanden bis zur Grenze, komme ich beim ersten auf 9 Möglichkeiten, beim zweiten bei 8, beim dritten auf 7 Möglichkeiten und beim vierten auf 6 Möglichkeiten. Addiere ich die zusammen komme ich also auf 30 Arten wie man den Zollstock zu einem Dreieck knicken kann. Allerdings scheint das auch nicht zu stimmen, da ich hier noch andere Möglichkeiten übersehen habe.

Hier das Bild zur Aufgabe:

Hallo Leute,

Ich muss ein Aufgabe in Mathe machen aber ich verstehe es komplett nicht. Das hat der Lehrer nicht gut erklärt und wir hatten nicht viel Zeit um uns mit diesem Thema gut zu beschäftigen. Ich werde mich sehr auf eure Antworten freuen ♥

Aufgabe: Die quadratische Pyramide wird 4 cm von der Spitze entfernt parallel zur Grundfläche abgeschnitten.

Ferner gilt: G1 = 64 cm² und h = 10 cm

Berechne das Volumen des entstehenden Pyramidenstumpfes, indem du das Volumen der oberen Ergänzungspyramide vom Volumen der ursprünglichen Pyramide abziehst.

Ich danke euch im Voraus

Liebe Grüße