Flächeninhalt Quadrat berechnen?
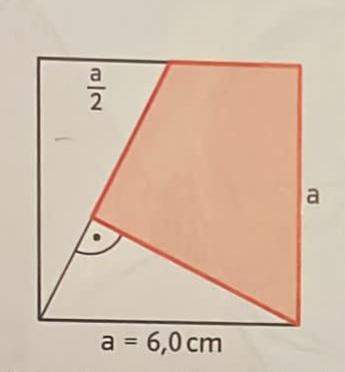
Hallo und zwar soll ich davon den Flächeninhalt berechnen und stehe jedoch gerade voll auf dem Schlauch. Also eine Fläche ist 18. Das heißt die Links oben. Habe ich berechnet indem ich 6/2*6 gerechnet habe. Stimmt das soweit und wie kommt ich auf das andere Dreieck?
6 Antworten
Da ist das Dreieck
Quadrat ist doch rel. einfach. Seitenlänge*Seitenlänge = Flächeninhalt
Und ein Dreieck in dem Quadrat hat halt den halben Flächeninhalt.
Jetzt sehe ich erst das Bild: Du musst einfach nur den Flächeninhalt der Dreiecke berechnen. FlächeninhaltQuadrat - FlächeninhaltDreiecke = FlächeninhaltGesucht
Das ist mir ja klar. Aber ich weiß nicht, wie ich das andere Dreieck ausrechne
Schon aber es sind ja nicht 2 mal die gleich großen Quadrate
Da man eine Seitenlänge (6cm) und einen Winkel (90°) des unteren Dreiecks hat, kann man über den Sinus die Seitenlängen und somit auch den Flächeninhalt von diesen berechnen. Zieht man die Flächeninhalte der beiden Dreiecke von den 36 cm2 ab, erhält man die Lösung.
Also eine Fläche ist 18
ein Quadrat besteht aus 6 Teilflächen
ziehe die Wurzel aus 18, damit hast die Länge und kannst rechnen
wäre Volumen
da das Bild später kam, funktioniert das nicht
da wirst über den Pythagoras und Winkelfunktion rechnen müssen.
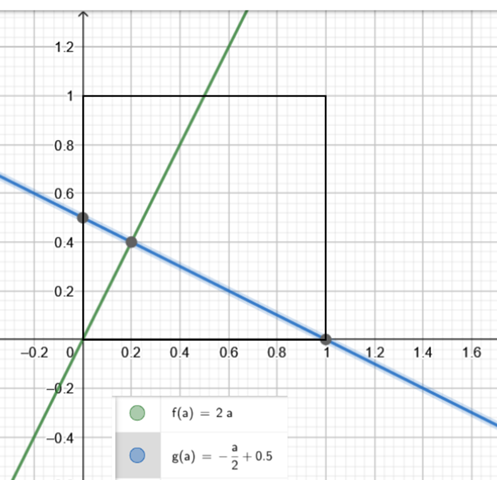
Eine Idee ist zwei Funktionen aufzustellen. Das Quadrat soll eine Seitenlänge von genau a = 1 lang sein.
g(a) = 2a
f(a) = -a/2*a + 0,5
Schnittpunkt g(a) = f(a) den kannst du ablesen. Auf deine Figur angewandt wäre der Schnittpunkt bei 0,2*a und die Höhe wäre 0,4*a
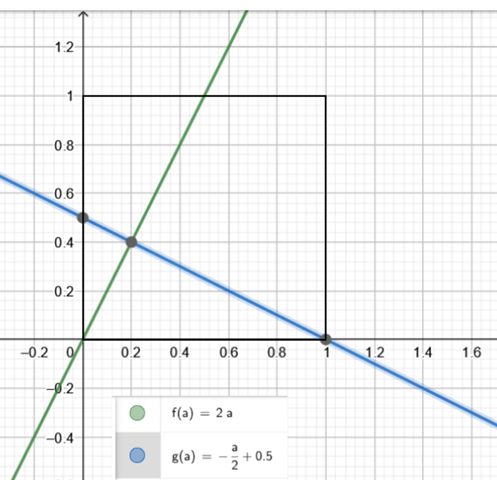
Das untere Dreieck hat damit eine Fläche von A = 0,5* G * h = a * (0,4a) = 0,2a²
Das Dreieck links oben hat eine Fläche von A =0,5* a * a/2 = 0,25a²
Deine gesuchte markierte Fläche ist dann groß:
A = a² - 0,2a² - 0,25a² = 0,55a²
Und was für eine Länge habe ich dann?