Quadrat in viertel Kreis?
Hi Leute komme einfach nicht weiter, wäre super lieb wenn ihr mir helfen könntet. Habe gefühlt schon alles probiert. Lg
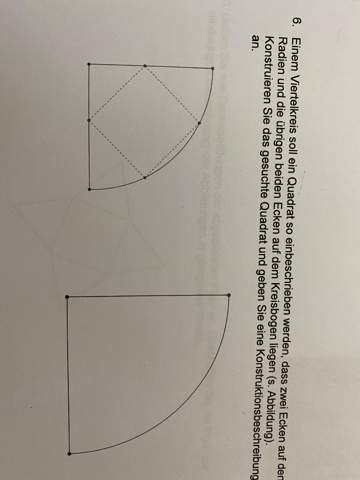
2 Antworten
Seit wann kann GF denn die Grafiken wieder vergrößern? Oder ist es hier ein Zufall?
Meine Konstruktionsbeschreibung stimmt anscheinend nicht, obwohl ich derzeit nicht sehen kann, warum nicht.
Also ziehe ich sie zurück!
Da ich nicht weiß, ob GF aus der Bearbeitung eine Nachricht macht, hier ein Dummy-Kommentar, damit es gesichert ist.
Das funktioniert leider nicht, da die beiden Eckpunkte links und unten des gesuchten Quadrats die Kreisradien nicht halbieren.
Hallo,
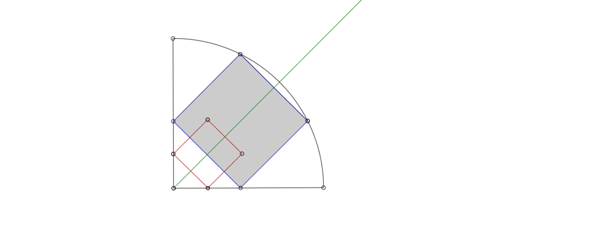
konstruiere zunächst die Winkelhalbierende (grün) des Viertelkreises.
Danach eine Senkrechte zu dieser Winkelhalbierenden nicht zu weit vom Mittelpunkt des Viertelkreises entfernt. Die Schnittpunkte dieser Senkrechten mit den beiden Schenkeln des rechten Winkels, der den Viertelkreis begrenzt, sind eine Seite des Hilfsquadrats (rot). Du ergänzt die drei anderen roten Seiten.
Nun verbindest Du den Kreismittelpunkt einmal mit dem Eckpunkt des roten Quadrats, der ganz oben steht, durch einen Strahl und den Mittelpunkt mit dem Eckpunkt rechts durch einen zweiten Strahl.
Die Schnittpunkte dieser beiden Strahlen mit dem Bogen des Viertelkreises ergeben die Eckpunkte oben und links des gesuchten Quadrats (blau), das Du entsprechend ergänzt.
Hier noch ein zweites Bild mit den eingezeichneten beiden Strahlen (rot):
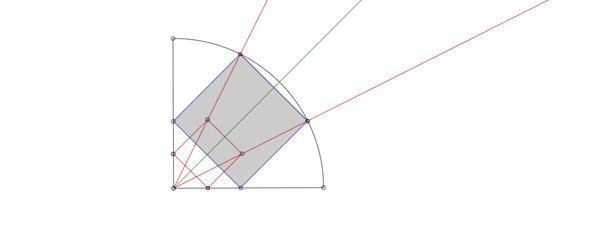
Herzliche Grüße,
Willy
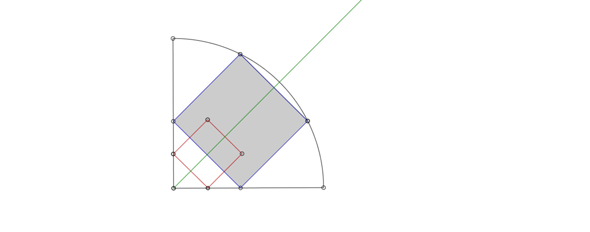
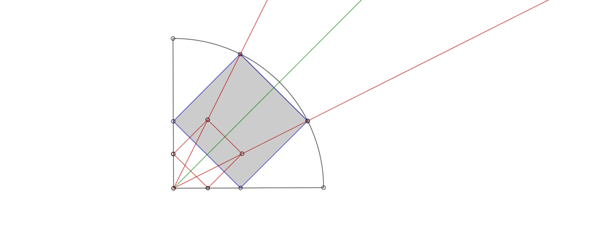
Und das funktioniert, weil auch die beiden äußeren Ecken des Hilfsquadrats auf einem Viertelkreis (mit kleinerem Radius) liegen. Eine zentrische Streckung führt dann auf den großen Viertelkreis.
Wenn man es vorgeführt bekommt, ist es einfach. Wie kommt man darauf? Oder ist das eine Standardaufgabe, wenn man zentrische Streckungen behandelt?
Mir sind schon des öfteren Aufgaben begegnet, die über Hilfskonstruktionen gelöst werden. Bei mir war es einfach Erfahrung.
Du bist mega Schlau, wie kommt man nur darauf selbst frage ich mich