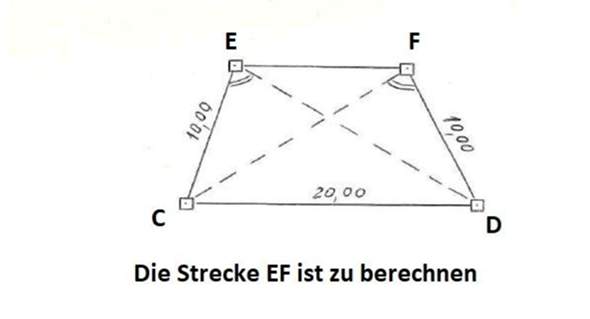
Strecke berechnen Viereck Winkel?
Weiß jemand die Antwort darauf..
5 Antworten
ED = CF = √300 = 17,32... (Pythagoras)
Winkel DCF = Winkel EDC = 30° (Sinus)
S = Schnittpunkt der Diagonalen
Winkel ESC = 60°
Winkel FCE = 30°
EF² = 10² + 300 - 2 * 10 * √300 * cos(30°) (Kosinussatz)
EF = 10,00
Sei M der Mittelpunkt der Seite CD und damit auch der Mittelpunkt des Theleskreises über CD. Der Radius des Thaleskreises ist 10. Auf diesem Kreis liegen auch E und F.
Wegen DM = DF = MF = 10 ist das Dreieck MDF gleichseitig, das Dreieck CME ebenfalls.
Da die Winkel DMF und MCE beide gleich sind (60°), sind MF und CE parallel. Aus Symmetriegründen sind auch CM und EF parallel. Damit ist CMFE ein Parallelogramm und EF = CM = 10.
Hallo,
ohne weitere Angaben ist das Viereck nicht eindeutig konstruierbar und somit auch nicht zu berechnen.
Herzliche Grüße,
Willy
Dann geht's. Strecke DE ist Wurzel (20²-10²)=Wurzel (300).
Strecke EF ist dann Wurzel (300-100)=Wurzel (200)=10*Wurzel (2).
Nee, ist doch 10. Ich hatte einen der beiden rechten Winkel falsch eingezeichnet.
Hallo,
hier hast Du noch eine Zeichnung nach Konstruktion mit den eingezeichneten Größen:
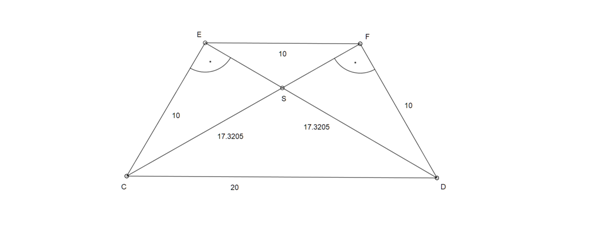
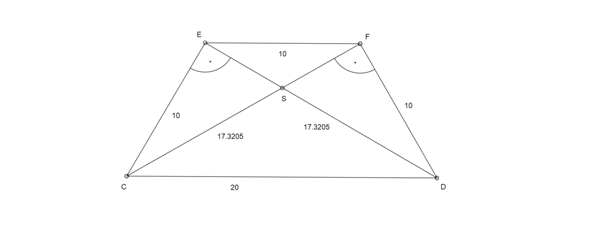
Die Angaben sind nicht ausreichend
Die Winkel oben sollen rechte Winkel sein. Geht es dann ?