Exponentialfunktion – die neusten Beiträge

Heyy, nochmal ne kurze Frage. Gestern hab ich ja meine Klausur in Mathe geschrieben. Jetzt mach ich mir über alles nen Kopf und das bereitet mir am meisten Sorgen, da ich nicht weis ob das prinzipiell falsch ist.

also ich sollte ja den Wertebereich von f(x)= -x^3 + 2 und g(x)=0,5x+1,5 angeben. Da das ja beide Expotenzialfunktionen mit ungeraden Exponeten sind ( die eine lineare Funktion und die andere eine Parabel 3. Ordnung) hab ich erstmal geschrieben y ist Element der reellen Zahlen. Nun hab ich aber auch noch geschrieben: y ist uneingeschränkt im Definitionsbereich. Klar, grundsätzlich hat der Definitionsbereich was mit den x und nicht den y Werten zu tun. Aber lasst mich erklären was ich mir dabei gedacht habe:

Ja, das sind beides Funktionen die unendlich viele Y Werte annehmen können. Aber zu jedem Y Wert gehört ja auch ein x Wert. Wenn es also einen Y Wert der Funktion gibt, dessen zugehöriger X Wert außerhalb des Definitionsbereiches liegt, gibt es dann diesen Y Wert für die Funktion oder nicht? Wenn dieser Y Wert dann nicht existiert, dann ist der Wertebereich im gewissen Sinne ja schon durch den Definitionsbereich beschränkt.

Ist meine Denkweise einfach falsch oder ist das vielleicht überflüssig mit hin zuschreiben, bzw. Kann meine Mathe Lehrerin mir dafür einen Punkt abziehen?

Hallo habe Probleme bei der folgenden Aufgabe. Jede Hilfe wäre nützlich. Ich möchte aber nicht nur einen Lösungsweg auch wenn dieser bereits weiter hilft sondern fände auch eine Erklärung zu den Schritten nützlich da ich die Aufgabe auch verstehen will. Danke im Voraus!

Aufgabe:

Nach starken Regenfällen im Gebirge steigt der Wasserspiegel in einem Stausee an.Die in den ersten 24 Stunden nach den Regenfällen festgestellte Zuflussgeschwindigkeit kann nahrungsweise durch die Funktion f mit f(t)=0,25t3 -12t2 +144t beschrieben werden (t in Stunden, f(t)= in m3/h).

Berechnen Sie die Nullstellen von f sowie die Koordinaten der Extrempunkte von f erläutern Sie die Bedeutung Sie die Bedeutung der Ergebnisse

Die Stellen habe ich berechnet, jedoch fehlt mir die Erläuterung der Bedeutung. Kann mir jemand helfen?

Und wie bestimmt man den Zeitraum in dem die Zuflussgeschwindigkeit mindestens die Hälfte des Maximalwerts beträgt ?

erklären*

Hallo Community

Es wäre echt nett, wenn mir jemand bei def folgenden Matheaufgabe helfen könnte:) :

Die Funktion f(x)= In(1-x) ist angegeben. Man soll nun am Entwicklungspunkt f0=0 eine Taylorreihentwicklung der Funktion f(x) bis zum 3 nicht verschwindenden Glied durchführen. Von der Taylorreihe habe ich schon gelesen, weiß leider aber trotzdem nicht, wie diese Aufgabe zu lösen ist.

Ich freue mich besonders über ausführliche Antworten!😊

Kann mir das jemand knapp erklären? Ich Blick da nicht durch

nr. 23 a)

Aufgabe: Wo sind die Funktionswerte von f(x)= 1/xⁿgrößer als 400 bzw. kleiner als 0,05? 

a) n=1, n=3   b) n=2, n=4

Problem/Ansatz:

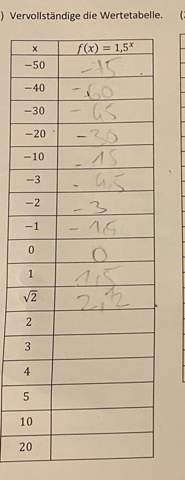
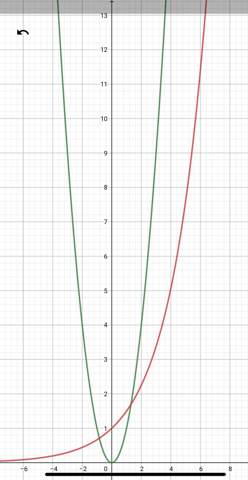
Wie löst man diese Aufgabe.

Schreibe Freitag die Klausur und hänge an dieser Aufgabe

Danke im voraus

A1 - b)… Den ersten Teil der Aufgabenstellung verstehe ich noch, da wird bloß die Ableitung gebildet und 0 für den x wert eingesetzt (Ergebnis müsste -3a sein)

aber der zweite Teil fällt mir schwerer

ich verstehe es so dass ich f‘(1) nach a Auflösen… es würde rauskommen 0 macht aber keinen Sinn auch vom grafen her (gtr)

wie kommt man voran, danke schonmal!

Woran erkenne ich anhand dieser Funktion ohne Taschenrechner, ob sie gegen +-unendlich oder gegen 0 verläuft?

Also bei x-> +∞ verläuft sie gegen 0 und x-> -∞ verläuft sie gegen -∞. Ich verstehe das iwie nicht weil das in Bruch ist.. Wie kommt man drauf

Wir haben als Thema gerade die momentane Änderung auzurechnen, wenn da steht "Es ist f(x)=3x^2. Bestimmen Sie rechnerisch die Ableitung von f an der Stelle." was wäre dann hier a?

Bestimme den Inhalt der Fläche, die vom Schaubild von f, der y-Achse und den Geraden g : y = -x -1 sowie h : x = 1/2 ln(2) eingeschlossen wird.

f(x) = -e^-2x -x -1

Falls ja: Geben Sie ihren Verkauf und ihre Funktionsgleichung an.

Leute, ich komme da nicht weiter. Kann mir irgendwer helfen?

Kann mir jemand bei dieser Aufgabe helfen?

 g(x) = tan(x), gesucht ist die Stammfunktion G(x).

Ich weiß leider nicht, wie ich vorangehen soll.

Danke schonmal im Vorraus. Stern bekommt ihr dann, wenn ichs vergeben kann.

LG

Moin,

ich verstehe mal wieder eine Aufgabe nicht, deshalb bitte ich jemandem diese mir zu erklären.

In einem Forschungslabor werden Algen gezüchtet. Diese verdoppeln sich täglich. Zu Beginn liegt eine Algenmasse von 8g vor.

-Wie entwickelt sich die Algenmasse in den ersten 5 Tagen?

-Wie viel Algenmasse könnte man nach dem vierten Tag entnehmen, ohne dass sich der Bestand verringert?

-Wie hoch ist die stündliche Rate?

Ich habe für die folgende Aufgabe a)

1.für lim x -->unendlich=0

2.für lim x --> minus unendlich=0/"unendlich"

3.für lim x -->0 =1/"unendlich"

herausbekommen. Das Problem ist ich weiß nicht ob das stimmt.

Falls ja dann bitte sagen was ich im Fall von durch unendlich aus Ergebnis machen muss und falls nein bitte eine Erklärung wie man es macht.

(Und wo kann ich sicher sagen wo die Fkt. stetig ist)?

Kann mir jemand erklären wie ich diese Aufgabe machen muss? Bisher hab ich bei a) 120 • a^4,5 = 45, aber ich denke dass es falsch ist

f(x) = 2e^x + x^2 - 2x +1

f'(x) = 2e^x + 2x - 2

Ist das so richtig?

Und wie kann ich jetzt die Extrempunkte berechnen? Ich weiß nicht wie ich die Gleichung mit dem E Teil lösen soll

Sind Quadratische-Funktionen ein Teil von Potenzfunktionen? Falls nicht was ist der Unterschied zwischen den beiden?

LG

Ich habe de Ableitung angegeben: f'(x)=x-1 und Integral von 0 bis 2 f=5 Wie kann ich jz durch diese Infos den Term herausfinden? Ich habe f' integriert weiter weiß ich nicht

Bsp:

F(x)= -x⁴-8x²+9

Nullstellen kann ich rechnen, hier sind sie

x1= -1 und x2= 1

Aber wie bekomme ich y raus?

Um eine Skizze der Funktion zu machen brauche ist Y

Hallo ich hab eine Textaufgabe , weiß leider nicht wie ich sie lösen soll. Ein Kapital von 20.000€ wird mit einem Zinssatz von 5% jährlich verzinst.
a) Vor wie vielen Jahren betrug das Kapital bei gleichem Zinssatz 15.000€

b) In welchem Jahr nimmt das Kapital erstmal um 5000€ zu?

Wie genau kommt man darauf? Es geht um die Normierung einer Wellenfunktion.

Könnte mir jemand helfen die Umkehrfunktion zu lösen?

Die erste Aufgabe ist: Bestimmen sie für die Funktion die Stelle, an dem sie den Wert 4 hat. Die Funktion wäre dann f(x)=x^3

Die zweite Aufgabe: Bestimmen Sie n so, dass der Graph f(x)=x^n durch den Punkt verläuft, hier wäre es E (0,1/0,001) oder B (-3/9)

Wie löst man folgende Exponentialfunktion? Bin ein wenig verwirrt weil es zwei Exponenten mit x drin gibt. Vielleicht hat ja jemand eine Idee

Meine Gleichung ist: 1013.25 × 0.99987 ^ x

Dabei geht es um die Halbierung des Luftdrucks, wie kann ich das ausrechnen?

Ich mache hin und wieder in meiner Schullaufbahn auf logarithmusaufgaben.

Manchmal stoße ich auf aufgeben, wenn man die Zinsen berechnen muss, wo ich den logarithmus berechnen muss. Aber da war es mir dann im vornherein nicht wirklich klar.

Ich will nicht wissen, wie, sondern wann man den logarithmus berechnet. Woran erkennt man, dass das von mir verlangt wird? Das wird irgendwie kaum besprochen.

Hallo, ist das richtig?

Danke im Voraus

Ich habe eine Hyperbel (besser gesagt zwei… . Siehe Bild unten, ->Habe ich selber zusammengestellt). Meine Frage: Ich soll dazu eine Funktionsgleichung der Form „a*x^2+c“ aufschreiben. Wie gehe ich jetzt vor? Wie finde ich „a“ bzw. „c“ heraus? Gibt es Regeln, damit ich das immer schaffe?

Danke im Voraus!

Hallo, kann mir jemand bei diesen Aufgaben helfen?

hey weiß jemand wie ich das lösen könnte?

Heyy :)

Ich war die letzte Mathestunde leider krank und meine Klasse hat die allgemeine Exponentialfunktion durchgenommen. Auch, wie man den Funktionsterm von einem Graph ablesen kann und auch wie man den Graph mit dem Term zeichnet.

Ich habe das leider nicht verstanden und wollte hier mal um Hilfe bitten.

Danke schon mal :))

Wie wäre die aufleitung von e^2x?

Ich habe irgendwie das Gefühl dass die Ableitung einer Funktion mit den binomischen Formeln zusammenhängt, natürlich unter Anwendung des Konzeptes der Infinitesimalrechnung und von Grenzwerten. Denn a²+2ab+b² stellt ein Quadrat dar welches in zwei kleinere Quadrate und zwei Rechtecke geteilt wird. Wenn man nun aber den Flächeninhalt der Flächen 2ab und vor allem b² ( das alleine reicht ja schon) gegen Null laufen lässt bleibt praktisch nur 2a übrig. Wenn man jetzt statt „a“ den Buchstaben „x“ verwendet fällt sofort auf dass man mit 2x praktisch die Ableitung von x² zu erhalten scheint. Wenn ich dann auch noch Newtons vereinfachte Schreibweise betrachte statt „(a+b)²“ „(1+x)²“ zu schreiben sticht das für mich noch mehr heraus. Das Gleiche funktioniert scheinbar auch bei höheren Graden, auch wenn ich nicht alle ausprobiert habe.

Auf Youtube gibt es diverse Videos, wie man die Produktregel anwendet, jedoch wird nicht erklärt, warum man mitten in der Ableitung Klammern setzt.

Daher meine Frage, wann setzt man bei der Produktregeln beim ableiten klammern?

Wie berechne oder lese ich die Steigung an den Stellen -2 und 1 ab?

Die Funktion ist =x hoch 2

Heyyy,

an meine Matheprofis hier:D, ich hab vorkurzem erst mit meinem Mathe Studium begonnen und bin bisschen lost, also kann es sein, dass ich hier mehrere Fragen stellen werde. Würde mich freuen wenn ihr mir helfen könntet:)).

Zur Frage, unten habe ich ein Bild gepostet, was die Aufgabe zeigt. Habt ihr vielleicht Tipps für mich, wie ich die Übungen mit wirklich absolut Beginner kenntnissen trotzdem meistern kann? Falls ihr Videovorschläge habt würde ich mich freuen, ansonsten, nehme ich auch jede andere Art von Hilfe an:D. Also, wie sollte ich hier am besten vorgehen?^^

Eine Bakterienkultur hat anfangs 1000 und eine Verdoppelungszeit von 3 Minuten. Die Bakterienkultur Y hat anfangs 2000 und eine Verdoppelungszeit von 4 Minuten. Berechne den Zeitpunkt an dem beide gleich viel haben?

stecke bei dieser aufgabe fest >.<

Hallo,

ich brauche Hilfe bei der Aufgabe, ich finde nichts wie man sie lösen kann.

wäre sehr dankbar für Vorschläge wie man die Aufgabe 7 lösen kann 😊

lg

x -> + ∞ gillt f(x) -> + ∞

x -> - ∞ gillt f(x) -> + ∞

Bei Potenzfunktion mit geraden positiven Exponent also : f(x) = x^4

x —> + ∞ gillt f(x) -> + ∞

x -> - ∞ gillt f(x) -> - ∞

Bei Potenzfunktion mit einem ungeraden positiven Exponenten also :

f(x) = x^3

x -> + ∞ gillt f(x) -> + ∞

x -> - ∞ gillt f(x) -> + ∞

Bei Potenzfunktion mit geraden und negativen Exponenten also..

f(x) = x ^-4

x -> + ∞ gillt f(x) -> + ∞

x -> - ∞ gillt f(x) -> - ∞

Bei Potenzfunktionen mit einem ungeraden und negativen Exponent.

Hab ich das Richtig gemacht, bzw.. das Verhalten der Funktionen im Unendlichen richtig beschreiben?

Ich weiß nicht wie ich hier vorgehen soll.Es wäre super, wenn mir jemand die Lösung vorgeben könnte und auch erklärt wie man darauf kommt :)

Hallo ich habe Probleme mit der 8

Ich verstehe es garnicht und wollte nach Hilfe fragen bzw wie man da vorgeht zum rechnen ?
dankee

Ich bräuchte mal bitte Hilfe bei den Aufgaben. Was ich alleine gemacht habe, ergibt keinen Sinn…

Lena bekommt 50 Milligramm eines Medikamentes verabreicht. Nach jeder vollen Stunde bekommt sie weitere 3 Milligramm des Medikaments. Ihr Körper baut pro Stunde 8 Prozent des Medikaments ab.

a) Die Menge des Medikaments in Lenas Körper soll für die ersten 3 Stunden dargestellt werden. Skizziere einen passenden Funktionsgraphen.

b) Berechne die Menge des Medikaments in Lenas Körper für die nächsten 36 Stunden jeweils zur vollen Stunde. Nutze eine Tabellenkalkulation.

c) Erstelle auf dem gleichen Arbeitsblatt der Tabellenkalkulation eine Wertetabelle zur Funktion f mit f(t) = 20 + 30 • 0,85'.

d) Vergleiche die Werte aus der Tabelle in b) und der Wertetabelle in c).

e) Anna behauptet: „Die Funktion f passt nicht zur Situation." Hat sie recht? Begründe.

danke falls jemand helfen kann

Die Bevölkerungszahl beträgt 7.300.000 im Jahr 2010, jährlich nimmt sie um 1,6% (1,06) zu.
a) Berechne, im welchen Jahr die Bevölkerung neun Millionen Menschen erreicht.

b) Berechne, im welchen Jahr 20 Millionen Menschen dort wohnen.

Meine Formel wäre:

N(t) = 7.300.000 x 1,06 hoch 9, jedoch stimmt diese nicht, gibt es dafür was anderes?

das gelbe ist x^-4

In der Aufgabe steht nicht dass wir das erklären sollen. Wir sollen einfach nur den Graphen digital zeichnen. Mehr nicht.

Aber trotzdem interessiert mich das warum das so aussieht

kanns mir wer erklären?

Hallo, ist der Graph der Exponentialfunktion mit der Basis 2 einfach nur f(x)=2 oder f(x)=2x?

Danke schonmal!

Die Aufgabe ist die n-te Ableitung von f(x)=2^x zu finde, aber ich verstehe gar nicht was ich machen soll oder wie ich vorangehen muss??

Wenn ich die hyperbel im koordinatensystem hab wie kann ich dann die formel einleiten zu der grundformel? die ja lautet a•(x-d)²+e

was muss ich tun/ablesen jnd wo in die formel einsetzen damit ich die komplette formel rauskriege?

Ich habe zunächst die ableitung von f(x) gebildet = f'(x)=-2x. Was mach ich jetzt als nächstes? Aufgabe 23 Nr d

F(x)= x³-3x²-16x+48

Wenn ich die Funktion ausklammern möchte, muss die 48 in die Klammer?

x ( x²-3x-16)+48 oder x ( x²-3x-16+48)???

In welcher Zeit verdoppelt sich das Guthaben von 10000 € bei einer Verzinsung von 4 %?

z.B. bei x : 4 + x

dort ist ja die waagrechte Asymptote y=1 und die senkrechte Asymptote x= -4

Ich habe ein Physik Arbeitsblatt bekommen.

Dir Aufgaben bringen mich zum verzweifeln, kann mir jemand helfen ?

Heyy, wie würde man ableiten, wenn man beispielsweise folgende Brüche ableiten müsste?

Welche Regeln sind dabei zu beachten?

a) 1/a x⁴

b) a/4 x²

Hallo, ich verstehe es immer noch nicht ganz, wie ich diese Exponentialfunktionen vereinfachen kann. Nie weiß ich, welche Regeln ich anwenden muss. Vielleicht kann mir jemand weiterhelfen.

a) 2ln(x) - ln(2x)

b) (e^3ln(a) - 2e^ln(a))² * a^-2 + 4a²

Wie viel Bakterien gibt es, wenn sie sich alle 20 Minuten verdoppeln und das 16 Stunden lang?

Vielen Dank!

Wenn ich die Funktion e^x (x-a+1) habe, wie kann ich die Funktion nullsetzten, um die Nullstelle zu berechnen.

Weil meine Lehrerin hat nur, dass in der Klammer nullgesetzt und das e^x einfach ignoriert, weil es ja immer größer null ist. Aber kann man das einfach so ignorieren.

Hallo,

wir schreiben in einer Woche eine Mathe Klausur und haben als Übung u.a. diese Aufgabe bekommen. Ich verstehe sie leider nicht und habe keine Ahnung wie man die Graphen den Funktionen zuordnen kann. Kann mir jemand helfen?

Vielen Dank im Voraus

Hallo liebe Community,

ich sitze gerade an einer Abiaufgabe und komme nicht auf die Ableitung.

kann mir jemand erklären wieso aus f(x)= 7200x^2*e^-0,25x f’(x)= 7200*(-0,25x^2+2x)*e^-0,25x wird? Mir ist klar dass man die Produkt und kettenregel anwenden muss, aber ich scheine mich irgendwo ständig zu verrechnen, kann mir jemand eventuell eine kleinschrittige Rechnung zeigen?

danke!

Geht das überhaupt

Wie ist die erste und die zweite Ableitung von der Funktion f(x)=x hoch 2 mal e hoch x?

Wie kommt man auf die -2,5x?

Woher die -10x ?

Ich verstehe nicht warum (e hoch 0.5) hoch x verwendet werden kann. Das entspricht ja etwa 1.64, das ist nicht 1.5
Ergo was heisst wachstumsrate?

ausgedrückt wird.

f(x)= 2e^(-1/2*x)+2x

Welche Gerade ist Asymptote des Schaubilds von f?

Wie ist die Frage gemeint?

Wie bekommt man die Funktionsgleichung von der schwarzen und der roten heraus?

Habe bei dem blauen Graphen 2^x+1 heraus (hab es bei Geogebra kontrolliert)

Bin bei dem roten Graphen genauso vorgegangen wie beim blauen, aber es kommt ein komplett falsches Ergebnis heraus.

Ich hoffe, dass ihr mir dazu weiterhelfen könnt.

Hey ich bereite mich für Mathe vor und die 1. Frage war was man allgemein von einer Funktionsvorschrift versteht. Das habe ich auch aufgeschrieben. Die 2. Frage lautet einfach "Was ist die Funktionsvorschrift?"

Wird die allgemeine gemeint?

Kann mir die bitte jemand nennen?

Dankeschön!

Die Wasserrose vermehrt sich auf einem See mit 8 ha Größe. Die bedeckte Fläche nimmt wöchentlich um 30 % zu. Anfangs sind 150 m^2 der Oberfläche bedeckt.

Ich hätte gedacht durch eine Funktionsgleichung gedacht, die ein beschränktes exponentielles Wachstum dargestellt

Bestimmen Sie die Stelle x, an welcher die Funktion f den Wert y annimmt.

f(x)=2•4^x y=4

komme nicht auf den Rechenweg :(

Woher weiß man ob eine Exponentialfunktion streng monoton fallend oder streng monoton wachsend ist?

Ich würde mich über eine Antwort freuen.

Woher weiß ich, welche Definitions– bzw. Wertemenge eine Exponentialfunktion hat?

Würde mich über eine Antwort freuen.

Hallo, ich benötige eure Hilfe zur folgenden Aufgabe;

gegeben sind die Funktionen ;

f(x)= 2 x 1,2^x und g(x)= 1,5 x 1,4^-x

diese Funktion soll ausgerechnet werden, um den zeichnerisch bestimmten Schnittpunkt rechnerisch zu bestätigen

Es wäre super, wenn jemand mir den Rechenweg aufzeigt und erklärt, da ich ihn nicht verstehe und weder durch das Buch oder mit Hilfe von YouTube auf das richtige Ergebnis komme.

vielen lieben Dank schon einmal im Voraus!

Wie kommt bei c auf die 1/5 ?

klar wegen alle 5 Stunden trotzdem versteh ich nicht ganz wieso es zb nicht 5 ist oder nur x und dabei wär dann x= vergangene Zeit alle 5 Stunden

Hallo,

wenn ich einen Graphen einer e-Funktion vor mir habe, wie finde ich heraus, ob der Graph in y-Richtung gestreckt oder gestaucht ist und wenn ja, was der Streckungsfaktor ist?

danke schon mal:)

Die Bestände zweier Ameisenkolonien können durch die Funktionen A(t)=5000-2000*e^-0,2t und B(t)=5000-3,2*(t-25)^2 erfasst werden.

a) Wann sind die Kolonien gleich groß?
b) Wann ist Kolonie A doppelt so groß wie Kolonie B?
c) Wie entwickeln sich die Kolonien langfristig? Wo liegt die Gültigkeitsgrenze von Modell B?

Bei der a) weiß ich, dass man beide Funktionen gleichsetzen muss. Wenn ich alles zusammenfasse sieht das bei mir so aus:

e^-0,2t= 1/625t^2-2/25t+1 |ln

-0,2t=-0,08

t=0,4

kann man das so machen? Hab alles was nach dem „=„ in Taschenrechner bei der ln Taste eingesetzt.

Bei der b) habe ich den Ansatz A(t)/B(t)= 2

Wenn ich hier alles kürze was man kürzen kann sieht das so aus:

e^-0,2t/ -3,2t+160t=2

Ist das bis jetzt so richtig? Wenn ja wie geht es weiter? Wenn nein was muss ich machen?

Ich schreibe morgen eine Arbeit und hänge schon länger an dieser Aufgabe hier.

Hallöchen.

Ich habe diese Aufgabe vor mir und kann mir selbst nicht helfen:

Eine Bakterienkultur wächst exponentiell. Um 8 Uhr waren es 2300 und um 12 Uhr 36200. Wie viele Bakterien waren es um 9 Uhr, um 10 Uhr und um 13.30 Uhr?

Kann mir jemand behilflich sein?

Der Führerschein naht?

Olafs Vater möchte 1.000€ zu 4,25% in einem Sparvertrag anlegen. Olaf ist 9

a) Olafs Vater plant für den Führerschein 1.900 € ein. Wann hätte er den Sparvertrag abschließen müssen? Bestimme den Zeitpunkt möglichst genau

b) in 8 Jahren möchte Olaf seinen Führerschein machen. Wie hoch hätte bei gleichem Zinssatz das Startkapital sein müssen, damit ihm ein Guthaben von mindestens 1.900 € zur Verfügung stehen wird?

Wie rechnet man die Aufgaben?

Wie funktioniert der Rechenweg von b) und c) ?

Ein Kondensator der Kapazität C wird über einen Widerstand R aufgeladen bzw. entladen. Der Spannungsverlauf am Kondensator während des Aufladevorgangs wird dabei beschrieben durch die Funktion U mit U(t)= U₀* (1-e^{-1/ R*C *t}), der Spannungsverlauf während des Entladennvorgangs durch die Funltion U mit U(t)= U(0) * e^{-1/R*C *t}. Das Produkt von Widerstand R und Kapazität C wird als Zeitkonstante (tau) bezeichnet: tau = R * C

a) Um wie viel Prozent hat die Spannung am Kondensator beim Entladevorgang nach der Zeitkonstante tau abgenommen?

b) Man sagt der Kondensator ist nach der Zeit t=5 (tau) entladen. Wie viel Prozent der ursprünglichen Spannung liegen zu diesem Zeitpunkt noch am Kondensator an?

Kann mir jemand helfen bei dieser Aufgabe?

Ein Kondensator der Kapazität C wird über einen Widerstand R aufgeladen bzw. entladen. Der Spannungsverlauf am Kondensator während des Aufladevorgangs wird dabei beschrieben durch die Funktion U mit U(t)= U0* (1-e-1/ R*C *t), der Spannungsverlauf während des Entladennvorgangs durch die Funltion U mit U(t)= U(0) * e-1/R*C *t. Das Produkt von Widerstand R und Kapazität C wird als Zeitkonstante bezeichnet: = R * C

a) Auf wie viel Prozent der Spannung U0 hat die Spannung am Kondensator beim Aufladevorgang nach der Zeitkonstante zugenommen?

b) Man sagt, der Kondensator ist nach der Zeit t= 5 aufgeladen. Auf wie viel Prozent der angelegten Spannung U0 ist die Spannung am Kondensator zu diesem Zeitpunkt gestiegen?

Ich bitte um Hilfe und Erklärung, wie man das rechnen könnte

f(x)=2 × 4^x , y=4

Hi,
ich weiß nur, dass x ungefähr 5 ist… aber nicht wie man es auflösen soll

Mfg Lu

Hallo,

Die Aufgabe lautet:

"Zum Zeitpunkt t=1850 lebten auf der Erde y=1,17 Milliarden Menschen, t=1900 waren es bereits y=1,61 Milliarden und t=1950 y=2,50 Milliarden. Bestimmen Sie das mittlere Bevölkerungswachstum und berechnen Sie die erwartete Bevölkerungszahl für 2020. Nehmen Sie einen funktionalen Verlauf y = a · e^b·t an. Finden Sie die Antwort rechnerisch und zeichnerisch!"

ich habe da schonmal einen Ansatz, aber bin mir da echt nicht sicher. Ich glaube man muss nach e rechnen:

2,5Mrd=1,17Mrd*e^100

hierfür habe ich dann den Logarithmus angewendet

log100(2,137)=0,1649

wenn ich die Zahl aber wieder einsetze um die Lösung zu prüfen kommt was ganz anderes raus...kann mir da jemand vielleicht helfen?

ich danke sehr im Voraus <3

Habe folgende Ableitung: h'(x)=2e^2x-4

und muss davon die Extrempunkte berechnen, also h'(x)=0

Meine Rechnung:

0 = 2e^2x -4 | + 4

4 = 2e^2x | : 2

2 = e^2x

ln(2) = ln(2x)

ist das soweit richtig und wie kann ich das weiter lösen?

Hi, wir fangen gerade in Mathe ein neues Thema mit Verkettungen an und ich habe mir Beispiele angeschaut wie Funktionen neu gebildet werden, nur ich verstehe nicht wie es bei der Differenz eine +3 wird, wenn man doch eigentlich x^2+1 - x -2 rechnet und dann -1 daraus ergibt ?

Hallo,

ich gehe auf das technische Berufskolleg und unser nächstes Mathe Thema wird Exponentialfunktion sein. Ist das Thema einfach oder schwer? Hatte jemand schon Erfahrungen damit?

Hi,

bei der Aufgabe muss du jeweils die Wertetabelle ausfüllen. Muss ich um an den zweiten Wert dazukommen jeweils x•1,5 rechnen oder 1.5 hoch x. Hab echt ne schwere Zeit den Stoff nachzuarbeiten und würd mich echt über ne Antwort freuen.
FG

Hallo, ich muss eine Gleichung nach einer Variablen, hier "t" , auflösen. Krieg ich aber irgendwie nicht hin - mach ich etwas falsch oder geht das einfach nicht?

ab der letzten Zeile fang ich an Probleme zu haben.

Kann mir bitte jemand sagen, wie ich bei der Aufgabe auf den Wachstum komme. Also wie ich a bestimmen kann?

Hey,

also ich hab folgendes Problem…

ich schreibe am Freitag eine Klassenarbeit und in der kommen unter anderem auch Aufgaben wie hier nr. 6&8 dran. Ich kann grob einordnen welche Funktionen in welchen Quadranten gehören, dennoch weiß ich nicht genau, wie man die finale Entscheidung trifft.

Könnte mir vielleicht jemand anhand von 2-3 Beispielen pro Aufgabe oder so erklären, wie man genau vorgeht?

das Bild mit der Überschrift Kompetenz Check beschreibt, was in der Arbeit drankommt. Hier ist nr.1b ja eine ähnliche Aufgabe, jedoch finde ich viel einfacher. Hier hatte ich nämlich keine Probleme, da ich es anhand der Steile des Abflachens oder des Steigens bestimmt habe…

Danke im Voraus :)

Hallo - ich bräuchte Hilfe bei folgender Aufgabe, da ich nicht weiß, wie ich dabei vorgehen soll:)

Radioaktive Substanzen zerfallen exponentiell mit einer gewissen Halbwertszeit. Die Aktivität oder Zerfallsrate einer radioaktiven Stoffmenge ist die Anzahl der Kernzerfälle pro Zeiteinheit. Die Einheit dafür ist 1 Becquerel (1Bq), benannt nach Henri Becquerel, einem französischen Physiker. 1 Bq entspricht einem Zerfall pro Sekunde. Iod-131 hat eine Halbwertszeit von 8 Tagen. Eine bestimmte Menge dieser Substanz hat eine Aktivität von 48 kBq.

Ergänzen Sie die Lücken des folgenden Satzes so, dass eine mathematisch korrekte Aussage entsteht!

Die Aktivität ..., weil ...

Lücke 1

• ist nach 16 Tagen praktisch null
• ist nach 24 Tagen auf 6kBq gesunken
• nimmt pro Tag um 3kBq ab

Lücke 2

• drei Halbwertszeiten vergangen sind.
• eine Abnahme um 24 kBq innerhalb von 8 Tagen eine gleichmäßige Abnahme von 3 kBq pro Tag bedeuten.
• die Abnahme pro Halbwertszeit 24 kBq beträgt.

Aufgabe:

Der Anfangswert beträgt 3000, die Verdopplungszeit ist 2,5 Jahre. Wie hoch ist der Bestand nach 10,5 Jahren?

Meine Lösung:

ca. 5513.8

Buch Lösung:

55138

Was habe ich falsch gemacht, bzw. Kann das jemand bitte mal vorrechnen?

LG Jakob