[#Mathe#] Exponentialfunktion Nullstelle berechnen?
Ich habe ein für mich unlösbares Problem.
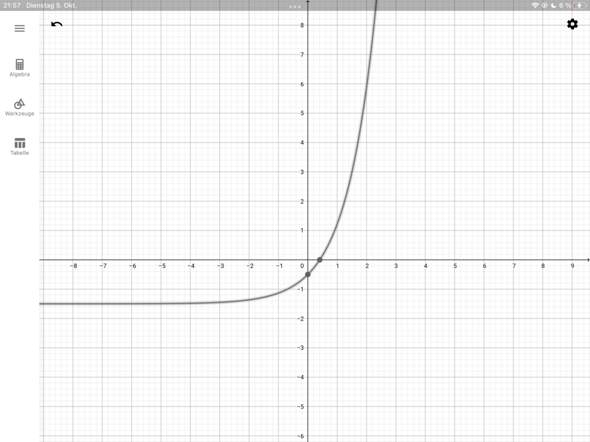
Bei dieser Aufgabe konnte ich die Nullstelle problemlos berechnen:

Schaubild des Funktionsterms:
Bei der kommenden Aufgabe (im Buch steht sie genau so da nur ohne -3 am Ende) hier drunter weiß ich nicht, wie ich die Nullstellen berechne, denn mit logarithmieren mit 2e^(-x) auf einer Seite würde ein einzelnes 1/2x rechts noch übrig bleiben.
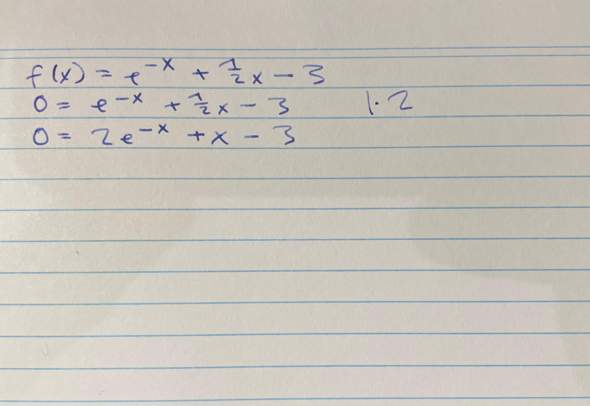
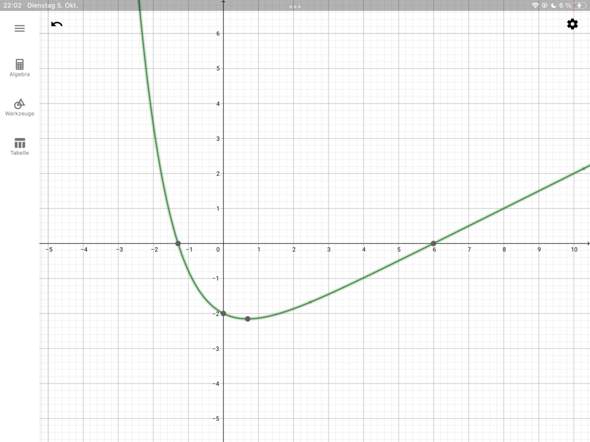
Das Schaubild (so wie es hier unten als Bild ist) ist auch im Buch dargestellt (nur ohne das -3 am Ende, ohne Nullstellen, diese Aufgabe möchte ich nur machen, um zu verstehen wie es geht). Vielleicht muss man noch einen Punkt ablesen, um auszurechnen/rechnerisch zu bestimmen dass es keine Nullstellen hat.
Vielen Dank, dass du deine Zeit für meine Frage investierst 💚
Mit freundlichen Grüßen 🙋♂️
3 Antworten
Soweit ich weiß (man möge mich korrigieren), ist es aussichtslos, Nullstellen von Funktionen zu berechnen, wo das x sowohl "normal" als auch als Argument einer e-Funktion oder Winkelfunktion vorkommt.
Ein Klassiker ist
https://photomath.net/s/81EnJ5
Das müsste die richtige Lösung sein.
Dort kannst du dir alle Rechenschritte erklären lassen.
Hoffe das hilft dir weiter
Mfg Sam
das mal 2 sein lassen, dafür mit e^x multiplizieren. Dann wir der erste Therm zu 1, der zweite zu 1/2 x*e^x und der dritte zu 3 e^x
Der zweite Therm ist die Lambert'sche Funktion. Um die nach x umzustellen gibt es laut google eine Standardlösung
https://kilchb.de/faqmath3.php
(allerdings hab ich dann doch nicht bachvollziehen können was da steht, Die Mathe II Vorlesung ist doch schon zu lange her und außerdem habe ich gerade keine Lust mir das Hirn zu verbiegen.