Schnittpunkt von 2 Logarithmusfunktion?
Ich möchte den Schnittpunkt von 2 Logarithmusfunktionen berechnen. Erster Schritt ist natürlich f=g:
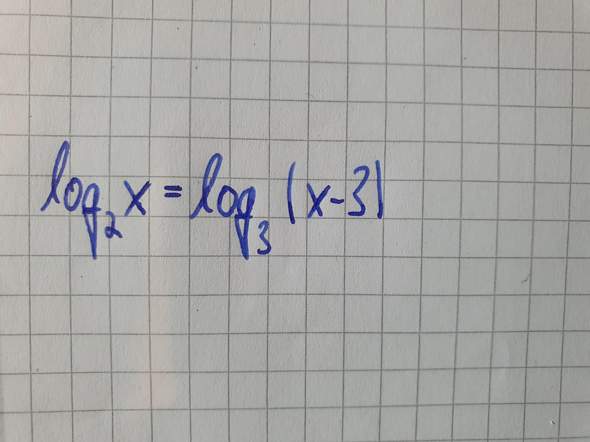
Aber wie geht es weiter? Einen Logarithmus auf die andere Seite bringen und dann ein Logarithmusgesetz anwenden, funktioniert nicht, da sie nicht die gleichen Basen haben.
3 Antworten
Mit dem Newton-Verfahren lässt sich die komplexe Lösung
9.86109533634565E-3+2.31440317668334*(i)
bestimmen.
Es gilt x = 0,0097+2,3144i sowie Konjugierte.
Man setzt h(x) := ln(x)/ln(2) - ln(x-3)/ln(3)
Mit x0 = 1 gewählt interiert man
x1 = x0 - h(x0)/h'(x0)
:::
xN-1 = xN-2 - h(xN-2)/h'(xN-2)
Stoppe, wenn
xN = xN-1 - h(xN-1)/h'(xN-1) = xN-1
Vor der gesamten Iteration lässt sich der allgemeine Term x - h(x)/h'(x) vereinfachen.
Der Taschenrechner muss auf komplexe Zahlen (CPLX) und Radiant (RAD) eingestellt sein, bei Dezimalzahlausgabe ohne automatischer Rundung (und nicht-symbolisch bei CAS Taschenrechnern).
Hilft Dir das?
Das ist ln(x) / ln(2) = ln(x-3) / ln(3).
https://www.wolframalpha.com/input/?i=ln%28x%29%2Fln%282%29+%3D+ln%28x-3%29%2Fln%283%29
ln(x-3) / ln(x)= ln(3) / ln(2)
https://www.wolframalpha.com/input/?i=ln%28x-3%29+%2F+ln%28x%29%3D+ln%283%29+%2F+ln%282%29
Für x gegen Unendlich konvergiert die linke Seite (von unten) gegen 1. ln(3) / ln(2) ist aber größer als 1, also gibt es keinen Schnittpunkt.
3^log2x= x-3
vielleicht bringt dich das weiter
man kann aber auch sagen:
log2x=log3x : log33
log2x=log3x: 1(da loga u = lg u : lg a)
also log2x = log3x also keine Schnittstelle
ich habe keine Ahnung weil wir das auch gerade erst machen also verlass dich bitte nicht drauf xD