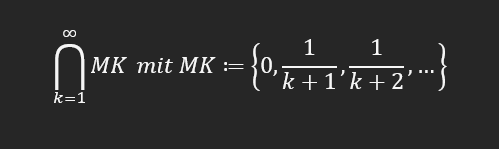Die 117, 158 und 447 sind mir gestern begegnet. Laut meiner bisherigen Recherche, sind dies Engelszahlen.

Welche andere Bedeutung könnten diese Zahlen noch haben, oder ist dies bereits die Erklärung?

--

https://engelszahlen.com/engelszahlen/engel-nummer-117/

geg. an = 1/n × cos(n)

Man sieht sofort, dass es eine Nullfolge ist. Die Cos. Funktion alterniert und 1/n geht gegen 0. Aber kann man das auch fundiert beweisen?

Hi,

es geht um folgende Folge:

 Erkennt ihr hier ein Zusammenhang? Arithmetisch und geometrisch ist es mMn nicht.

Vielen Dank schonmal für eure Hilfe.

29, -58, -55, 110, 113, -226, ?,

ich check das nicht. Was kommt dann und wieso?

In einer Nährlösung befinden sich ca. 1000 Einzeller einer Art, bei der es im Durchschnitt alle 20 Minuten zu einer Teilung kommt.

a) Geben Sie eine Folge an, die das explosive Wachstum dieser Art beschreibt.

b) Berechnen Sie, wie viele Einzeller nach 24 Stunden entstanden sind. Welche Länge ergibt sich, wenn man diese aneinander legt (Länge eines Einzellers: 0,001 mm)?

c) Nach welcher Zeit sind etwa 10 Millionen Einzeller vorhanden?

d) Welche äußeren Faktoren begrenzen das Wachstum?

Ich brauche unbedingt Hilfe zu d.

n*(n-1)

Hallo zusammen, ich habe gerade in Mathe Mengen und Zahlen zur Wiederholung und verstehe die eine Aufgabe nicht. Die Aufgabe lautet.

Wie löst man diese.

Beispiel e)

Bei den vorherigen Beispielen habe ich das letzte Folgenglied immer in das explizite Bildungsgesetz der geometrischen Folge eingesetzt und nach n aufgelöst. Hatte auch funktioniert, aber bei e) und f) klappt’s nicht.

Ich will dadurch auf die Summe der Reihe kommen. Also n in die Summenformel einsetzen.

1/64 = 2 * 0,5^(n-1)

liefert mir aber ein falsches Ergebnis.

Bitte um Hilfe!

Es gilt zu beweisen, dass 3^n-3 (n>=1) immer durch 6 teilbar ist. Im Internet sah ich mehrere Lösungsvorschläge, keiner der aussah wie meiner. Ich ging so vor:

Induktionsbeginn: 3^1-3=0/6=0 -> passt

Induktionsbehauptung: 6 teilt 3^n-3

Induktionsschritt: 3^(n+1)-3=3*3^n-3 -> man kann 3 ausklammern =3(3^n-1) und sieht nun, dass 3^n-1 immer gerade ist, weil 3^n ungerade ist und eine ungerade Zahl -1 wieder gerade. Damit hat man mit 3^(n+1)-3 eine sowohl durch 2, als auch 3 teilbare Zahl, die logischerweise auch durch 6 teilbar ist.

Hi,

ich suche immer in meiner Freizeit nach wegen Geld zu verdienen, mit Geld, das ich nicht brauche (niemand sollte mit wichtigem Geld spielen).

Und ich bin in Roulette auf eine Strategie gestoßen, wo man auf die zahlen Felder setzt, wo man immer, das dreifache zurückbekommt, mit einer zahlen folge(1,2,3,4,6,9,13,20,30,45,67,100) und ich brauchte eure Hilfe diese Zahlen folge fort zu Sätzen.

Ich habe euch das Video verlinkt.

https://youtu.be/xbouiKltYjc

Ich habe das Problem hier:

ich will eine reihe bilden für 0,99999.. die zu 1 konvergiert. Meine Reihe sieht so aus :

Sigma Zeichen :0,9*0,1^i

ich möchte bei der 10. Partialsumme eine immer genauere Annäherung an 1 haben . Wie jedoch mache ich das ,gibt da me Formel? Ich habe diese Formel : a0*1-q^n+1/q^n und komme dann nur auf das Folgenglied und nicht auf die Summe…

26=512

35=415

68=748

75=?

Setzen sie die Zahlenfolge um 2 Glieder fort

10 20 15 35 25 55

Hallo, leider war ich an dem Tag krank, als wir an der Uni Cauchy Folgen besprochen hatten und ich bin jetzt sehr verwirrt und verstehe dieses Beispiel nicht. Ich wäre sehr froh, wenn mir jemand helfen könnte :(

Vorallem steht oben noch in der Folge ein a mit kleinem n und -1.

Was soll das bedeuten? Ich weiß, dass "an" die Folge ist, aber die -1 dahinter verstehe ich nicht :( Außerdem verstehe ich auch nicht, was er weiterhin gemacht hat:(

Bräuchte die nächsten 3 Zahlen dieser Zahlenreihe 9,5,10,6,12,8,16

Vielen Dank

Hallo, ich habe bei dieser Aufgabe Probleme und wäre sehr dankbar für Hilfe :(

Wie komme ich darauf, dass die Folge von e

(1+1/N)^N= 1+N/1×1/N + ( N×(N-1) )/ 1×2 + ....

Auch als :

(1+1/N)^N = 1+1+1/1*2 + 1/ 1×2×3 + ....

dargestellt werden kann ?

Wie würde die arithemtische Folge 2. Ordnung aussehen mit der Formel:

a_n := a₀ + n * ã₀ + (n(n-1)/2) *d

Beispiel Zahlenfolge: 1,7,17,31,49

Soweit bin ich jetzt gekommen:

1 7 17 31 49

6 10 14 18

2 2 2

Ich verstehe aber nicht wie die Formel dazu aussieht?

Guten Tag,

ich habe Probleme bei der folgenden Aufgabe, kann mir da jemand weiterhelfen?

Aufgabe:

Seien (an) und (bn) zwei reelle Zahlenfolgen. Zeigen Sie, dass die durch c2n−1 := an und c2n := bn definierte Folge (cn) genau dann konvergiert, wenn die Folgen (an) und (bn) konvergieren und denselben Grenzwert haben.

danke im voraus!

Hallo,

zahlenreihe : 10,-5,25,-35,85,-155, ?

2,4,6,10,16,?

1,4,27,?,3125

4,12,6,12,36,18,36,?

20,23,28,14,17,22,11,?

18,9,11,14,7,9,12,?

ich bräuchte die Antworten für die ?. Kann das leider überhaupt nicht und bräuchte es für einen Einstellungstest.

LG

Nehmen wir an, dass sich eine Rakete mit 0.8c und das Licht mit c bewegt. Sie laufen parallel zueinander in die gleiche Richtung. Relativistisch addieren muss man ja, aber darf ich in dem fall klassisch subtrahieren, also annehmen, dass zwischen Rakete und Licht eine Relativgeschwindigkeit von 0.2c vorherrscht, oder muss man auch relativistisch subtrahieren?

Die Nummer 2 a) sowie b) verstehe ich nicht so ganz. Was ich weiß ist, das ich den limes (lim an n->unendlich) benutzen muss, aber wie ich die Zahlenfolge umformen soll weiß ich nicht so ganz, hab da sehr Schwierigkeiten. Kann mir einer das erklären.

Ich komm da nicht drauf. Habe es in irgendeinem Logiktest gesehen. Lösung gabs dazu nicht. Ich denke die 90 ist einfach falsch. Wie kann man denn wenn man von 16 auf 18 kommt von 18 auf 90 kommen?

Ich verstehe leider gar nichts.

morgen schreibe ich eine Klassenarbeit und lerne gerade ,aber diese Aufgabe hält mich gerade vom Weiterkommen ab

ich Zweifel gerade an a). Ich erkenne das es eine geometrische Folge ist da der werd immer im 1/2 kleiner wird. Aber ich weis nicht wie ich die Höhe des gesamten Gebildes berechnen soll

Wie löst man diese Formel auf löst man sie mit der rekursiven Formel auf, oder expliziten Formel auf? b(n)=(-2)xb(n-1) ; b(1)=1

ede Simkarte stehen 20 Ziffern un folgende Buchstaben un Buchstaben C/VE außerdem der Name des Dienstanbieters - was kann man daraus ablesen ????

Hallo, ich soll beweisen, dass für n Element aus N, es kein p Element aus N gibt, sodass: n<p<n+1 gilt.

Peano Axiome wurden noch nicht behandelt, dafür aber Körper- und Anordnungsaxiome. Ich habe vor, dies mit einer vollständigen Induktion zu beweisen. Dafür habe ich grundsätzlich 2 Ideen, ich weiß jedoch nicht, ob diese so sinnvoll sind.

1. N ist eine induktive Menge, das heißt es gilt „A(n) –> A(n+1)“. Ich habe für A(n)=(n−1)+1 geschrieben, aber darf man das so voraussetzen? Und dann müsste der Beweis für n+1gelten, da p jedoch <n+1 ist, gilt der Beweis nicht für p. 

oder

2. Ich führe die vollständige Induktion mit der gaußschen Summenformel durch, setze anstatt für n+1 p ein. Dann sieht man, dass diese Formel dann nur stimmt wenn p=n+1 gilt. Da p<n+1 ist und aufgrund von Trichotomie kann nur eine Relation gelten.

Ich würde mich über euren Rat freuen.

Ich muss in Mathe eine explizite Darstellung der oben genannten Zahlenfolge aufstellen. Ich habe die rekursive bereits, da man immer das vorherige folgenglied mit n addieren muss : an +1 ( nach unten gestellt) = an +n

zum Beispiel : für n = 1 ( in oben genannte Formel einsetzen )

a1+1 = a2 = a1 +1

a2= 0+1 = 1 somit ist a2 = 1 ( passt wie oben in der Zahlenfolge )

nun will ich aber die explizite Darstellung. Im Internet steht etwas von dreickszahlen und einer gaußschen summenformel. Die explizite wäre danach : an= n(n-1) / 2

jetzt verstehe ich nicht, wie man darauf kommt. Diese explizite Darstellung ist richtig, aber wie kommt man darauf. Vor allem das mit durch 2 dividieren ?Und auch das(n-1) Steht das für das folgenglied, das vor dem an folgt?

Hallo,

Ich verstehe nicht, wie man auf 1/((n+1)(n+2)) kommt, also der dritte Term von links, da man ja eigentlich an n/n+1 nur (n+1) hinzufügt

Ich sehe sehr oft zufällig im Alltag die Zahl 444, auch wenn ich es nicht darauf anlege, z.B. wandert mein Blick beim Spazierengehen zufällig auf ein Kennzeichen eines Autos wo die Zahl 444 enthalten ist, oder ich schaue sehr oft zufällig gerade dann auf die Uhr wenn es 14:44 ist. Aber auch abwegigere Situationen, wie z.B. dass diese Zahl dann in der Browserleiste oben im Code einer Internetadresse enthalten ist und ich genau auf diesen Abschnitt schaue, oder die Koordinaten irgendeines Ortes enthalten diese Zahl usw. Geht sogar so weit, dass die Zahl dann beispielsweise in Filmen die ich sehe auftaucht, z.B. eine Tür auf der "Room 444" steht - ich fühle mich also sprichwörtlich von der Zahl verfolgt.

Hat jemand ähnliche Erfahrungen, natürlich auch mit anderen Zahlen gemacht? Hattet ihr das Gefühl dahinter steckt eine spirituelle Botschaft, falls ja welche?

Ich bin im Internet über diese Zahlenfolge gestolpert und habe einfach absolut keine Idee wie diese zu vervollständigen ist. Kommt jemand von euch drauf? Es würd es wirklich gerne verstehen!

Hi, ich will unbedingt wissen wie man diese Zahlenfolge weiterführt und wie man darauf kommt.( eine Formel wäre nett)

1; 4; 12; 33; 88

Hallo,

wie bekomme ich die explizite Bildungsvorschrift aus einer rekursiven Bildungsvorschrift?

In meiner Aufgabe lautet die rekursive Bildungsvorschrift: a1=1; an+1=2 • an (Siehe Bild, Aufgabe b).

Ich habe folgende Zahlenfolge herausgefunden: 1, 2, 4, 8, 16, 32, 64, 128, 256,... (hoffe mal die ist richtig)

Wie bekomme ich jetzt die explizite Bildungsvorschrift heraus?

Guten Abend,

Ich soll eine Zahlenfolge lösen und als Summe zusammen fassen, zweiteres ist kein Problem, bloß bei der Folge komme ich nicht weiter. Ich hätte im ersten Anlauf 2hoch n gesagt, jedoch fehlt dafür zwischen 1 und 4 die 2.

Könnt ihr da helfen?

1, 4, 8, 16, 32, 64, 128, 256

Oder hat der Prof einfach die 2 vergessen?

Ich habe schon alles Mögliche probiert.

Danke für eure Hilfe

Kann mir bitte jemand Schritt für Schritt erklären wie man die rekursive Darstellung für wine Zahlenfolgen mit Brüchen findet. Mein Beispiel: 1, 1/2, 1/3, 1/4, …

Es geht um folgende Zahlenfolge:

1 2 3 5 7 11 _

Die Löung: 13 (Primzahlen)

Meine Lösung:

15 (+1+1 —> 2 dann 3, +2+2 —> 5 dann 7, +4+4 —>11 dann 15) also immer verdoppeln (1;2;4;8 usw.)

Wäre meine Lösung auch richtig, wenn man nur die Zahlenfolge fortsetzen soll?

Schreibt bitte nicht sowas wie eine Duzentilliarde eins oder so.

...

Quinquagintizentilliarde

Duzentillion

Duzentilliarde

... (Was kommt danach ?)

Die Frage im Titel bezieht sich auf Aufgabe 3 und 4.

Bei 3. aber ganz allgemein - mir ist nicht ganz klar, wie diese Zahlenfolge aussehen soll.

Und bei 4. ist eben die Sache mit dem Faktor a. Oder ist das Zufall, dass a als Vorfaktor gewählt wurde? Hat er gar nichts mit der Bezeichnung der Folge zu tun?

Danke im Voraus!

Ich verstehe es mit den brühen nich💁🏼

Hey, ich bräuchte Hilfe beim Bildungsgesetz einer Folge:

3, 33, 333, 3333 usw. (ich weiß wie es wahrscheinlich weiter geht, aber ich weiß die Formel nicht!)

Wenn es geht, explizit und rekursiv.

Danke schön:)

Ich brauche Hilfe bei den folgenden Aufgabe.

Die Seitenlänge des ersten Quadrates ist 1m. Täglich kommt eine Generation kleinerer Quadrate dazu, deren Seitenlänge nur noch ein Drittel der vorherigen Quadrate beträgt.

A) Berechne den Umfang der Pflanze Q1 Q2, Q3, Qn.

B) Berechne den Flächeninhalt der Pflanzen Q1, Q2, Q3, Qn.

ich weiß nicht, wie ich vorgehen soll.

Danke im Voraus :)

Hallo, ich möchte gerne aus eigenem Interesse wissen, ob es eine Zahlenfolge gibt, die arithmetisch UND geometrisch ist. Mich würde auch interessieren, wie diese Zahlenfolge aussehen könnte.

Danke im Vorraus :)

Hallo, ich brauche für meinen Matheunterricht eine Zahlenfolge, die weder arithmetisch noch geometrisch ist.

Wäre toll, wenn mir jemand helfen könnte und mir ein Beispiel geben könnte.

Danke im Vorraus

Hallo

Ich habe Probleme meine Aufgabe zu lösen unzwar soll es um drei weitere fortgeführt werden und ein Bildungsgesetz erstellt werden ich bin auch nach Vielen Versuchen nicht darauf gekommen.

1,16,81 und 256

Hallo liebe Community!

Bin gerade bei einer kniffligen Aufgabe und komme alleine nicht weiter. Schafft es vielleicht jemand von euch einen Rechenweg/Muster zu erkennen?:)

3, 9, 11, 23, 43, 77, 143

Hier: 1, 2, ?, 3, ?, 6, ?, 8, 9

Meint ihr Engelszahlen sind echt? Beispielsweise 111 finde ich unmöglich...

„Die Engelszahl 111 bedeutet, dass deine Gedanken wahr werden. Stelle sicher, dass du keine unerwünschten Gedanken in deinem Kopf hast. Dies ist die Art und Weise, wie deine Engel dich warnen, auf die Dinge zu achten, an die du denkst. Sie können sehr schnell zur Realität werden, wenn du nicht vorsichtig bist.“

Andere Engleszahlen sind realistischer haha aber trotzdem.

Einige sagen es wäre totaler Quatsch andere meinen es wäre ein Zeichen der Engel und dem Universum.

Über jegliche Hilfe wäre ich dankbar. Es kann auch sein, dass es nichts bedeutet.

Rom liegt doch viel näher an Deutschland

Hi,

Ich möchte gerne wissen, wo/womit man alle Kombinationsmöglichkeiten von einer Reihe von Buchstaben und Zifferrn herausfinden kann(Nein ich versuche nicht irgend jemandes passwort etc. zu knacken), dies beinhaltet auch groß- und Kleinschreibung von Buchstaben. Hier ein Beispiel einer Möglichen "Symbolreihe"

vOX892hjnBHUK878JN982nk7zNZUnykj73hskj98msioj3idj3o

Gruß,

David

habe folgende Reihe:

0,5; 0,75; 0,875: 0,9375; ...
Wie komme ich von irgendeinem Wert dieser Reihe in den darunterliegenden oder darüberliegenden, bzw. wie findet man das Glied dieser Zahlenfolge heraus?
Danke für Deine Antwort im Voraus (-:

30 10 7 21 24 8 5 ?

die Summe der Zahlenreihe 1, 2, 4, 8, 16, 32, 64, 128 berechnet man mit 128 x 2-1.

Wie berechnet man die Summe der Zahlenreihe 1, 3, 7, 15, 31, 63, 127?

Danke für Eure Antworten

Zahlenfolge: Beispiel für "monoton wachsend und Grenzwert bei 7"?

Guten Abend,

Ich suche eine Zahlenfolge, welche monoton wachsen ist und einen Grenzwert a = 7 besitzt. Eine Zahlenfolge zu erstellen, die monoton wächst ist für mich kein Problem. Das wäre ja zum Beispiel "(an) = 2+(n-1)", doch ich komme nicht darauf, wie ich es mit dem Grenzwert hinbekommen soll..

Ich würde mich über ein Tipp, bzw. evtl auch ein Beispiel sehr freuen!

Danke!

Luise hat sich eine vierstellige Zahl gedacht. Pierre versucht, sie herauszukriegen. Seine bisherigen Versuche waren alle falsch, aber Luise hat ihm Tipps gegeben.

7 6 4 2 — Keine der Ziffern ist korrekt.

2 7 4 1 — Eine Ziffer ist korrekt, sie steht aber an der falschen Stelle.

4 1 3 2 — Zwei Ziffern sind korrekt, aber beide stehen an der falschen Stelle.

9 8 2 6 — Eine Ziffer ist korrekt und steht auch an der richtigen Stelle.

5 0 7 9 — Zwei Ziffern sind korrekt. Eine davon steht an der richtigen Stelle, die andere nicht.

Welches ist die letzte Ziffer von Luises Zahl?

(A) 0

(B) 1

(C) 3

(D) 5

(E) 9 

Hallo zusammen,

ich verstehe nicht wieso bei dieser Zahlenreihe "36" gesucht wird, könnt ihr mir helfen.

wie viele Möglichkeiten gibt es, 5 verschiedene Zeichen, also eine mögliche Kombination aus 59 Buchstaben (groß u. klein), 10 Ziffern und den Sonderzeichen, zu bilden.
zB. sK8.-1 oder als)2 oder irgendeine andere. muss eine unendlich große Zahl sein xD
sorry wenn ichs verwirrend erklärt habe, hoffe ihr wisst was ich meine^^

Die Frage sieht vielleicht auf den ersten Blick verwirrend aus, aber es gibt sehr logische Gründe für diese Frage:

1. Bei den Zahlen von 11 bis 19 unterscheiden sich bei der Aussprache nur 'Elf' und 'Zwölf' von den Zahlen Dreizehn bis Neunzehn. Wäre das nicht der Fall würde man von 'Einzehn' und 'Zweizehn' sprechen (diese Frage wurde auf GF schon gestellt).
2. Ab 20 Gild dann zusätzlich das man immer 'und' zwischen der Zahl und der Zehnerstelle setzt z. B.: Einundzwanzig, Zweiundzwanzig, Dreiundzwanzig...

Warum alles so kompliziert machen, damit ist es für Kinder und Ausländer doch nicht logisch.

Vereinfacht könnte man es so darstellen, dass man das 'und' immer einsetzt und die Spezialwörter 'Elf' und 'Zwölf' weglässt, dann hätte man immer die gleichen Regeln:
Einundzehn, Zweiundzehn, Dreiundzehn...
Einundzwanzig, Zweiundzwanzig, Dreiundzwanzig... (wie man es kennt)

Auch könnte man das Prinzip der Zahlen 13-19 immer anwenden und das 'und' weglassen:
Einzehn, Zweizehn, Dreizehn...
Einzwanzig, Zweizwanzig, Dreizwanzig...
Eindreisig, Zweidreisig, Dreidreisig...

Ich finde es oft unpraktisch dass Sprachen, so viele nicht vereinheitlichte Spezialregeln haben, die es notwendig machen viel zu lernen, was oft nicht notwendig wäre. Es kommt mir manchmal so vor, als gehe es nur darum viel zu lernen, obwohl Effizienz immer im Vordergrund stehen sollte!

Hallo,

wie viele Möglichkeiten gibt es bei einer 3-Stelligen Ziffernkombination, wenn man 2 Ziffern schon weiß?

Also ein 3-stellige Ziffernkombination hat 1000 Möglichkeiten, aber um wieviel verkleiner sich die Möglichkeiten, wenn man z.B. die 2 und 6 schon kennt?

Danke im Vorraus!

Gruß

Hallo,

ich bin momentan dabei Koreanisch zu lernen, die kleineren Zahlen weiß ich bereits, allerdings habe ich gerade Schwierigkeiten mit den größeren Zahlen. Und zwar bei den (originalen?) koreanischen zahlen (nicht die sino koreanischen). Von 1-99 weiß ich alles, allerdings habe ich dann für 100 einmal 온 und einmal 백 gefunden. 백 ist ja auch 100 bei den sino koreanischen Zahlen, allerdings habe ich es auch bei den Originalen gefunden und nun frage ich mich, was denn nun stimmt. Außerdem weiß ich nicht, wie es dann weiter geht ( z.B 101 und 111). Wenn 온 stimmt, wären das dann 온열 und 온열하나 ? Und zuletzt habe ich noch die Frage, was denn 200, 300, 400, 500, 600, 700, 800 und 900 heißt.

Ich hoffe, man kann verstehen, was ich meine und dass es ist zu verwirrend ist. Ich würde mich sehr freuen wenn mir jemand weiter helfen kann.

LG Lotta !

Hallo zusammen,

ich bin neu hier und würde mich sehr freuen, wenn mir jemand kurzfristig bei einem Problem helfen kann. Meine Freundin hat morgen ein Assesment Test und wir zerbrechen uns gerade bei der folgenden Zahlenreihe den Kopf:

22 - 46 - 86 - 236 - 62 - 64 - 286

kennt hier jemand die Lösung und besonders den Lösungsweg?

vielen Dank für eure Hilfe :)

Markus

Hallo liebe Mathegenies und vielleicht auch nicht Mathegenies,

ich habe mir einige Gedanken über die Zahl Pi gemacht.

Wie wir alle wissen, ist Pi unendlich lang, also könnte theoretisch alles passieren, z.B eine Zahlenfolge mit 1000 Mal 9 innerhalb Pis (Ich hoffe das ist verständlich, stelle die Frage auf dem Handy und möchte nicht so viel tippen, bitte verzeiht mir :-)

Ich suche jetzt aber nach folgender Zahlenfolge (die folgende Eigenschaften haben muss):

Sie soll sich zwei Mal wiederholen

Sie fängt beim Anfang (also 3,141...) an und endet beim Anfang der Wiederholung, die die gleiche Zahlenfolge umfasst (also von 3,141... bis zur Wiederholung)

Ist bisschen schwer zu erklären, aber ich hoffe ihr versteht es

Also theoretisch wäre ja die Wahrscheinlichkeit unendlich niedrig, da immer wenn es keine Wiederholung gibt, eine weitere Zahl dazukommt und es unwahrscheinlicher wird, dass es sich wiederholt. Da Pi unendlich lang ist, müsste es unendlich oft unwahrscheinlicher werden.

Also ich habe ich zwei Fragen: Kann so eine Wiederholung überhaupt stattfinden und wenn ja bzw. nein warum?

Ich bitte euch ernsthafte Antworten zu geben, die auch wirklich hilfreich sind und keine nervigen Kommentare wie z.B "was für eine blöde Frage" oder "ja denke schon" da dadurch die Frage als gelöst gesehen wird, da es bereits Antworten gibt.

Ich danke euch und habe versucht, die Frage so gut ich konnte zu formulieren.

Vielen Dank im Voraus

Xydru

1>10>11>100>101>???

Warum sagt man in Europa Million, Milliarde, Billion, billarde....

Und in America

Million, Billion, trillion ...?

Ich bin nun in der 11. Klasse und habe einen neuen Mathelehrer bei dem ich leider nichts wirklich verstehe. Er hat uns jetzt so ziemlich in das Thema Zahlenfolgen eingeworfen und das Ganze ziemlich schnell erklärt sodass ich viele grundlegende Sachen nicht wirklich verstehen konnte.

Was ist denn nun überhaupt ein Grenzwert? Die zahlreichen Online-Erklärungen sind auch alle recht kompliziert formuliert. Ist das ein Wert der nie erreicht wird bzw. den man nicht genau berechnen kann?

Und eine weitere Sache, die ich nicht verstehe ist das Epsilon( ε). Wofür steht das bzw was gibt es an?

Ich bin am verzweifeln und wäre für jede Antwort sehr dankbar:)

Mit Begründung!!

N‘Abend.

Ich habe eine Liste voller Postleitzahlen, die ich gerne nach „Größe“ sortieren möchte. Sodass wenn Leute drauf gucken, sie schnell rausfinden ob ihre PLZ mit unter den aufgeführten steht und nicht die ganze Liste durchgucken müssen. Momentan ist das ganze nämlich nach Entfernung zum Ausgangsort sortiert.

Kann mir jemand sagen, wie ich das hinbekomme? :D

LG

Hallo, ich benötige Hilfe beim Lösen eines Zahlenrätsels.

Jemand eine Idee, was A, C und D sein könnten, und wie der Lösungsweg ist?

Also wie berechne ich diese?

(Es geht um explizite Zahlenfolgen)

Mit freundlichen Grüßen

Setze die Zahlenfolge in beide Richtungen jeweils 3 Zahlen fort: ... 27,36,46,57,69 ...

Hi,

Ich bin absoluter Anfänger in Sachen Programmierung und muss für meine Hausaufgabe (Imperative Programmierung) ein Programm schreiben, dass von einer Zahlenfolge mit positiven ganzen Zahlen, das Maximum, das Minimum oder den Mittelwert bestimmen soll. Die Zahleneingabe soll über die Konsole erfolgen. Das Ende einer Zahlenfolge soll durch eine negative Ganzzahl signalisiert werden. Im Endeffekt geht es mir hauptsächlich um die Eingabe der Zahlenfolge, bei der ich einfach nicht zurecht komme.

Hat jemand eine Idee, wie ich dies umsetzen kann?

Die Zahlenfolge lautet: 0, 3, 8, 15, 24, 35, 48...

es steigert sich halt am Anfang um 3 und danach immer um 3+2 und nach jedem mal kommt eine 2 hinzu. Wie schreibt man das als Formel auf, z.B an=?

Hallo Zusammen,

gleich vorweg, das ist keine Hausaufgabe oder so, nur ein Rätsel welches ich einfach nicht knacken kann... Und es fuchst mich total.

Kann mir vielleicht jemand einen Lösungsansatz verraten, oder 1 oder 2 Reihen vorgeben? Ich finde einfach keinen Einstieg bei den vielen Möglichkeiten.

Danke und LG

Setzt die Zahlen von 1 bis 9 jeweils viermal in das Diagramm ein.

Gleiche Zahlen grenzen Waagerecht und senkrecht niemals aneinander, wohl aber diagonal. Kommen je Reihe und Spalte Zahlen öfter als einmal vor, wird ausdrücklich darauf hingewiesen.

A: Die 1 und die 2 kommen jeweils zweimal vor.

B: Die 7 kommt zweimal vor.

C: Die 1 und die 4 kommen jeweils zweimal vor. Die Summe der sechs Zahlen beträgt 25.

D: Von links nach rechts bildet sich eine aufsteigende Reihe von direkt aufeinanderfolgenden Zahlen.

E: Die Summe der sechs Zahlen beträgt 38.

F: Die 9 kommt zweimal vor, die 3 kommt nicht vor.

1: Die Summe der sechs Zahlen beträgt 22

2: Die 8 kommt zweimal vor. Die Summe der sechs Zahlen beträgt 29.

3: Die 7 kommt zweimal vor, die 3 kommt nicht vor.

4: Die 3 kommt zweimal vor. Die Zahl in A4 ist größer als die Zahl in B4.

5: Diese Spalte zeigt von oben nach unten eine aufsteigende Reihe von direkt aufeinanderfolgenden Zahlen.

6: Die Summe der drei obersten Zahlen lautet 6, und die Summe der unteren dre Zahlen ist 23.

Die Aufgabe heißt: Die Längen der drei Seiten eines rechtwinkligen Dreiecks mögen die ersten drei Glieder einer arithmetischen Zahlenfolge bilden. Der Flächeninhalt des Dreiecks beträgt 150 cm^2 . Welche Maße haben die drei Seiten und wie heißt das Bildungsgesetz der Zahlenfolge?

Temperatur Gesteins nimmt zum Erdinneren hin um etwa 3 grad je 100m Tiefe zu. In MittelEuropa herrscht in 25 min tiefe etwa 10 grad.

1. Welche Temperatur herrscht in 10 km tiefe?
2. in welcher tiefe siedet Wasser, aus welcher Tiefe kommt 45 grad warme thermalquelle.

Also Ich kann diese schon lösen, aber ich denke, dass der Dreisatz in Mathe LK nicht verlangt wird. Und ich kann diese Aufgabe irgendwie nicht mit Zahlenfolgen verknüpfen, die wir in der letzten stunde erwaehnt hatten

Ich muss am Donnerstag einen Aufnahmetest an einer Uni machen

es kommen auch Zahlenfolgen

habt ihr Tipps wie man die möglichst schnell und gut lösen kann?

Hallo!

Ich lerne für den MedAT und werde bei Wortflüssigkeit trotz vielen Übens einfach nicht besser. Habt ihr irgendwelche Tipps (außer Anfangs- und Endsilben zu finden und auf ei, eu, au usw. zu achten)? Und denkt ihr, dass man sich in diesem Untertest verbessern kann oder ist das sozusagen sowieso reine Kopfsache, die man nicht trainieren kann? Das hat mir mal nämlich ein Kollege gesagt und jetzt bin ich mir nicht sicher wie sinnvoll es ist sich überhaupt darauf vorzubereiten... :/

An alle, die diesen Test nicht kennen: Wortflüssigkeit ist dasselbe wie Anagramme lösen, dh man bekommt einen Buchstabensalat und muss diese Buchstaben zu einem sinnvollen Wort zusammensetzen. In meinem Test handelt es sich hierbei um deutsche Nomen im Singular.

Vielen Dank für jeden Tipp!

Alles Liebe

Ich stehe vollkommen auf dem Schlauch.

Aufgabe: Finde den Grenwzert für die Folge an (nein das ist kein Schreibfehler, ich weiß bloß nicht wie man das n nach unten rückt).

an=(2^n-5^n)/(2^(n+1)+5^(n+1))

Ich hab schon viele Varianten versucht...L'Hospital bringt nix, mit dem negierten Nenner erweitern ebenfalls und die Potenzgesetze hab ich auch schon alle durchprobiert. Wahrscheinlich übersehe ich irgendetwas und bitte daher um Hilfestellung.

Keines Beispiel : 2,6,18,54...
Wie komme ich jetzt da auf die direkte Formel ?

Gibt es da eine bestimmte Regel ?

Vielen Dank für eure Unterstützung ❤️

Die Aufgabe lautet die Zahlenfolge bis a(8) aufzuschreiben zu: a) a (n) = Anzahl der Teiler von n b) b (n) = Summer der Teiler von n c) c (n) = Produkt -||- d) d (n) = Anzahl aller natürlichen Zahlen, die kleiner als n und zu n teilerfremd sind.

Mir fehlt der Ansatz zum Aufstellen der zugehörigen Gleichung, es scheitert beim Ausdruck: "Teiler von n". Kann mir da jemand helfen? Schon einmal Danke im voraus. :)

Hallo zusammen!

Wie führt man die folgende Zahlenfolge fort, bzw. wie lautet eine mögliche Funktionsgleichung für die Zahlenfolge?

1, 3, 7, 8, 21, 49, 76, 224, 467, 514, 1155, 2683, 5216, 10544, 26867, 51510, 95823, 198669, 357535, 863317, 1811764, 1811764, 33185509, 54538862, 111949941, 227634408, 400708894, 1033162084, 2102388551, ...

Viele Grüße,

Elias.

Hey ich frage mich wie man diese Zahlenfolge herausbekommt und was die schritte sind, also was man rechnen muss.

Setze die Zahlenreihe fort: 7 21 14 42 28 ...

Ich möchte meiner Schwester drei schwierige Zahlenfolgen geben, die sie lösen muss. Sollen halt eine Reihe von Zahlen sein mit einem bestimmten Muster dahinter. Z.B.: 1;4;7;10;13;16 (immer +3) nur sollen die hakt schwer sein. Pls mit Lösung, also der Vorgehensweise, Danke! LG

Ich bekomme folgende Zahlenfolge nicht heraus:

8 - 64 - 4 - 64 - 2,8284 - 64 - 2,2974 - 64 - ... - ... -...

Man soll die letzten drei Zahlen angeben. Vermutlich ist es ganz einfach, aber ich komme nicht darauf.

Ich hoffe, jemand kann helfen. Danke im Vorraus!

1, 8, 27, 64, 125, ... Kann mir jemand weiterhelfen? Und SEHR WICHTIG sagt mir bitte wie ihr darauf gekommen seit. Danke im voraus! :)

Hallo

also ich muss einen java-code schreiben, bei dem zahlen aus einer schlange ausgelesen werden und umgedreht werden Das ist die genaue aufgabe: das Programm ZahlenUmdrehen, das eine beliebige Folge Zahlen aus einer Queue ausliest und mithilfe eines Stacks in umgekehrter Reihenfolge über die Methode ausgabeZahlenfolge() ausgibt.

Testen Sie das Programm mit der Zahlenfolge 10,4,6,7,3,5,1.

danke schonmal :)

Zahlenfolge: 1/-2/3/-4/5/-6

Uns wurde die explizite Form schon vorgegeben und wir sollen jetzt die rekursive daraus bilden. Explizit: an=(-1)^n+1 *n Es wäre super, wenn der Rechenweg nachzuvollziehen ist. Ein riesen Dankeschön schon im Voraus!

PS: Meine ganze Klasse verzweifelt an dieser Aufgabe. XD

Im Bild sind die aufgaben.

Es gibt noch eine Aufgabe, die ich aber hier rein schreibe. 1. Bestimmen Sie die ersten fünf Glieder und das allgemeine Glied an folgender Zahlenfolge : a ) jeder natürlichen Zahl n > 0 ist ihre um 2 verminderte Quadratzahl zugeordnet. Meine Lösung: n (hoch) 2 -2, also das Quadrat von n -2 und dann für n, die zahlen von 1-5 einsetzen und ausrechnen.