Wie lautet die rekursive Form der folgenden Zahlenfolge?
Zahlenfolge: 1/-2/3/-4/5/-6
Uns wurde die explizite Form schon vorgegeben und wir sollen jetzt die rekursive daraus bilden. Explizit: an=(-1)^n+1 *n Es wäre super, wenn der Rechenweg nachzuvollziehen ist. Ein riesen Dankeschön schon im Voraus!
PS: Meine ganze Klasse verzweifelt an dieser Aufgabe. XD
6 Antworten
a ᵢ ₊₁ = ‒ (aᵢ / |aᵢ|) ∙ (|aᵢ| + 1) = ‒ aᵢ ∙ (1 + 1/|aᵢ|)
Hmm, Rechenweg ist immer schwierig, aber ich würde als Rekursion konstruieren:
a_0 = 1
a_i+1 = -sign(a_i) * (|a_i| + 1)
Richtig, aber die Frage, ob es effektiver hinsichtlich der Komplexität (Rechenleistung) ist, stelle ich mal in den Raum. Man könnte als weitere Alternative statt (-1)^(|a_i|) auch (-1)^(i+1) nehmen. Ich denke aber, die Signumfunktion führt da direkter zum Ziel.
a[n]=(-1)^n * n = pow(-1,n)*n
a[n+1]=pow(-1,n+1)*(n+1) Nachfolger
Quotient: pow(-1,n+1)*(n+1)/[pow(-1,n)*n]=(-1-n)/n
a[n+1]=a[n]*(-1-n)/n
Nicht immer ist der Quotient einfach! Manchmal auch andere Funktionen (Differenz usw.)
Es gibt mindestens 4 Vorzeichenwechsel-Funktionen für Index n=ganzzahlig:
pow(-1,n)=cos(PI*n)=1-2*n+4*floor(n/2)=1 - n % 2 * 2
mit n%2 = n modulo 2 = n-2*floor(n/2) mit floor=Abrunden
wobei die Modulo Funktion rechentechnisch die schnellste ist (besonders bei großen n).
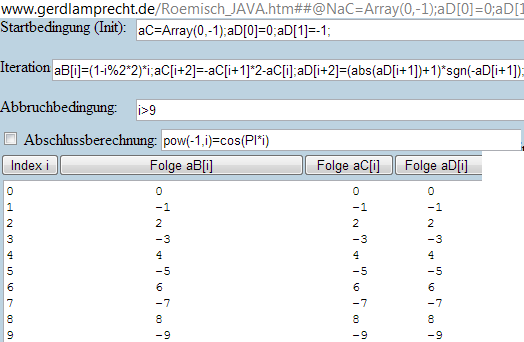
Beim online Iterationsrechner ist Index nicht n sondern i und a[n] ist aB[i]:
http://www.gerdlamprecht.de/Roemisch_JAVA.htm##@NaC=Array(0,-1);aD[0]=0;aD[1]=-1;@N@Bi]=(1-i%252*2)*i;@Ci+2]=-@Ci+1]*2-@Ci];aD[i+2]=(@AaD[i+1])+1)*sgn(-aD[i+1]);@Ni%3E9@N0@N0@N@P-1,i)=cos(PI*i)
siehe Bild
Besonderheit bei aC und aD: zum Start 2 Vorgänger nötig:
aC: weil Definition 2 Vorgänger velangt
aD: weil sgn(0)=0 alle anderen Argumente liefern Vorzeichen +1 oder -1
Besonderheit bei Verwendung von
aD[i+1]=aD[i]*(-1-i)/i; darf Index i erst bei 1 beginnen, da
1/0 = undefinierte Polstelle
Start: aD[0]=0;aD[1]=-1;
Iteration: if(i>0)aD[i+1]=aD[i]*(-1-i)/i;
(statt aD auch alles mit aB möglich)
Ich würds direkt ablesen:
sei f(n) gegeben.
wie kommst du zum nächsten?
+1 rechnen und beim ergebnis ein - davor bzw. mi (-1) multiplizieren.
also wenn du bspw f(n)=1 hast,
dann ist f(n+1)=(-1)*(f(n)+1)=-2
Und noch eine Variante, ohne Betrag und Sonderfunktionen wie Signum, dafür aber Rekursion mit zwei Vorgängern.
a(n+2) := - 2 * a(n+1) - a(n) und natürlich a(1) = 1, a(2) = -2.
Statt "-sign(a_i)" kann man auch "(-1)^(|a_i|)" nehmen.