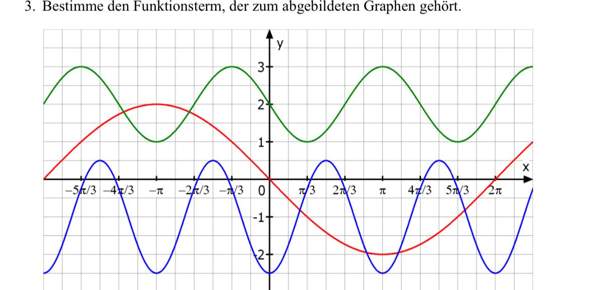
Hallo Leute
und zwar habe ich folgende Aufgaben bekommen, allerdings komme ich nicht wirklich weiter. Wir hatten das Thema noch nie und ich muss mich selbst damit beschäftigen, um es für die Klasse zu erklären, indem ich diese Aufgaben löse.
folgende Antwort habe ich für a), könnt ihr bitte kontrollieren, ob es richtig ist, weil ich bin mir nicht sicher, ob das mit mathematisch dargestellt gemeint war.
a) > Ein Rotationskörper ist ein dreidimensionaler Körper, der entsteht, wenn eine Fläche um eine bestimmte Achse rotiert bzw. dreht. Ein Beispiel für einen Rotationskörper ist ein Zylinder, der durch Rotation eines Rechtecks um die x-Achse entsteht. Ein Graph einer Funktion f(x) umschließt mit der x-Achse eine Fläche auf dem Intervall I = a, b. Diese Fläche rotiert um die x-Achse und bildet somit einen Rotationskörper. Das Volumen (V) eines Rotationskörpers, der durch die Rotation einer Funktion f(x) um die x-Achse entsteht, berechnet sich mit folgender Formel aus: V = π⋅a∫b f(x)² dx
Wobei a und b die Integrationsgrenzen der Funktion sind und f(x) die Funktionsgleichung des Graphen darstellt.
bei d) weiß ich auch schon wie ich vorgehe: Um auf das Gewicht eines Rotationskörpers zu kommen, braucht man nur das Volumen davon und die Dichte. Man multipliziert diese beide zusammen, und dann hat man das Gewicht des Glases. G = Vol • rho
Dafür brauche ich natürlich erstmal das Volumen
Jetzt brauche ich Hilfe bei b) und c)
Ich hoffe, dass mir jemand hier helfen kann. Das wäre sehr nett und würde mich freuen. Danke im Voraus :)