Gauß Integral?

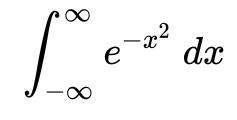
Wie berechne ich davon das Integral?

Answer 1

[LORDderANALYSE]

mihisu hat schon in seiner Antwort den normalen Weg erklärt, ich erkläre daher einfach mal zwei andere Wege.

Beide Wege beruhen darauf, dass wir die Stammfunktion bilden und dann die Integralgrenzen einsetzen.

Spezielle Funktionen

als PNG:

als LaTeX-Code:

\begin{align*}
&\text{Fehlerfunktion:}\\
&\quad \operatorname{erf}\left( x, y \right) \equiv \frac{2}{\sqrt{\pi}} \cdot \int_{x}^{y} e^{-\zeta^{2}} \operatorname{d}\zeta\\
&\quad \operatorname{erf}\left( x, y \right) = \operatorname{erf}\left( 0, y \right) - \operatorname{erf}\left( 0, x \right)\\
\\
&\text{Stammfunktion bilden: }\\
&\quad \int e^{-x^{2}} \operatorname{d}x = 1 \cdot \int e^{-x^{2}} \operatorname{d}x\\
&\quad \int e^{-x^{2}} \operatorname{d}x = \frac{2 \cdot \sqrt{\pi}}{2 \cdot \sqrt{\pi}} \cdot \int e^{-x^{2}} \operatorname{d}x\\
&\quad \int e^{-x^{2}} \operatorname{d}x = \frac{\sqrt{\pi} \cdot 2}{2 \cdot \sqrt{\pi}} \cdot \int e^{-x^{2}} \operatorname{d}x\\
&\quad \int e^{-x^{2}} \operatorname{d}x = \frac{\sqrt{\pi}}{2} \cdot \frac{2}{\sqrt{\pi}} \cdot \int e^{-x^{2}} \operatorname{d}x\\
&\quad \int e^{-x^{2}} \operatorname{d}x = \frac{\sqrt{\pi}}{2} \cdot \underbrace{ \frac{2}{\sqrt{\pi}} \cdot \int e^{-x^{2}} \operatorname{d}x}_{\text{nutze die Definition der Fehlerfunktion: } \operatorname{erf}\left( 0, ~x \right) ~\equiv~ \frac{2}{\sqrt{\pi}} \cdot \int_{0}^{x} e^{-x^{2}} \operatorname{d}x}\\
&\quad \int e^{-x^{2}} \operatorname{d}x = \frac{\sqrt{\pi}}{2} \cdot \operatorname{erf}\left( 0, ~x \right) + c_{1}\\
\\
&\text{Grenzen einsetzen:}\\
&\quad \int_{-\infty}^{\infty} e^{-x^{2}} \operatorname{d}x = \lim_{a \to \infty} \left( \frac{\sqrt{\pi}}{2} \cdot \operatorname{erf}\left( 0, a \right) \right) - \lim_{b \to -\infty} \left( \frac{\sqrt{\pi}}{2} \cdot \operatorname{erf}\left( 0, b \right) \right)\\
&\quad \int_{-\infty}^{\infty} e^{-x^{2}} \operatorname{d}x = \frac{\sqrt{\pi}}{2} \cdot \lim_{a \to \infty} \left( \operatorname{erf}\left( 0, a \right) \right) - \frac{\sqrt{\pi}}{2} \cdot \lim_{b \to -\infty} \left( \operatorname{erf}\left( 0, b \right) \right)\\
&\quad \int_{-\infty}^{\infty} e^{-x^{2}} \operatorname{d}x = \frac{\sqrt{\pi}}{2} \cdot \left( \lim_{a \to \infty} \left( \operatorname{erf}\left( 0, a \right) \right) - \lim_{b \to -\infty} \left( \operatorname{erf}\left( 0, b \right) \right) \right)\\
&\quad \int_{-\infty}^{\infty} e^{-x^{2}} \operatorname{d}x = \frac{\sqrt{\pi}}{2} \cdot \left( \lim_{a \to \infty} \left( \operatorname{erf}\left( 0, a \right) \right) - \lim_{a \to \infty} \left( \operatorname{erf}\left( 0, -a \right) \right) \right)\\
&\quad \int_{-\infty}^{\infty} e^{-x^{2}} \operatorname{d}x = \frac{\sqrt{\pi}}{2} \cdot \left( \lim_{a \to \infty} \left( \operatorname{erf}\left( -a, a \right) \right) \right)\\
&\quad \int_{-\infty}^{\infty} e^{-x^{2}} \operatorname{d}x = \frac{\sqrt{\pi}}{2} \cdot 2\\
&\quad \int_{-\infty}^{\infty} e^{-x^{2}} \operatorname{d}x = \sqrt{\pi}\\
\end{align*}

Reihenentwicklung

als PNGs:

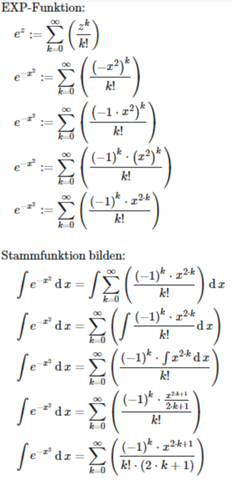
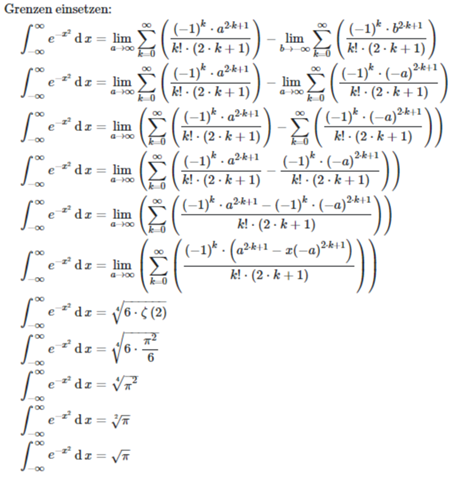
als LaTeX-Code:

\begin{align*}
&\text{EXP-Funktion:}\\
&\quad e^{z} := \sum_{k = 0}^{\infty} \left( \frac{z^{k}}{k!} \right)\\
&\quad e^{-x^{2}} := \sum_{k = 0}^{\infty} \left( \frac{\left( -x^{2} \right)^{k}}{k!} \right)\\
&\quad e^{-x^{2}} := \sum_{k = 0}^{\infty} \left( \frac{\left( -1 \cdot x^{2} \right)^{k}}{k!} \right)\\
&\quad e^{-x^{2}} := \sum_{k = 0}^{\infty} \left( \frac{\left( -1 \right)^{k} \cdot \left( x^{2} \right)^{k}}{k!} \right)\\
&\quad e^{-x^{2}} := \sum_{k = 0}^{\infty} \left( \frac{\left( -1 \right)^{k} \cdot x^{2 \cdot k}}{k!} \right)\\
\\
&\text{Stammfunktion bilden: }\\
&\quad \int e^{-x^{2}} \operatorname{d}x = \int \sum_{k = 0}^{\infty} \left( \frac{\left( -1 \right)^{k} \cdot x^{2 \cdot k}}{k!} \right) \operatorname{d}x\\
&\quad \int e^{-x^{2}} \operatorname{d}x = \sum_{k = 0}^{\infty} \left( \int \frac{\left( -1 \right)^{k} \cdot x^{2 \cdot k}}{k!} \operatorname{d}x \right)\\
&\quad \int e^{-x^{2}} \operatorname{d}x = \sum_{k = 0}^{\infty} \left( \frac{\left( -1 \right)^{k} \cdot \int x^{2 \cdot k} \operatorname{d}x}{k!} \right)\\
&\quad \int e^{-x^{2}} \operatorname{d}x = \sum_{k = 0}^{\infty} \left( \frac{\left( -1 \right)^{k} \cdot \frac{x^{2 \cdot k + 1}}{2 \cdot k + 1}}{k!} \right)\\
&\quad \int e^{-x^{2}} \operatorname{d}x = \sum_{k = 0}^{\infty} \left( \frac{\left( -1 \right)^{k} \cdot x^{2 \cdot k + 1}}{k! \cdot \left( 2 \cdot k + 1 \right)} \right)\\
\\
&\text{Grenzen einsetzen:}\\
&\quad \int_{-\infty}^{\infty} e^{-x^{2}} \operatorname{d}x = \lim_{a \to \infty} \sum_{k = 0}^{\infty} \left( \frac{\left( -1 \right)^{k} \cdot a^{2 \cdot k + 1}}{k! \cdot \left( 2 \cdot k + 1 \right)} \right) - \lim_{b \to -\infty} \sum_{k = 0}^{\infty} \left( \frac{\left( -1 \right)^{k} \cdot b^{2 \cdot k + 1}}{k! \cdot \left( 2 \cdot k + 1 \right)} \right)\\
&\quad \int_{-\infty}^{\infty} e^{-x^{2}} \operatorname{d}x = \lim_{a \to \infty} \sum_{k = 0}^{\infty} \left( \frac{\left( -1 \right)^{k} \cdot a^{2 \cdot k + 1}}{k! \cdot \left( 2 \cdot k + 1 \right)} \right) - \lim_{a \to \infty} \sum_{k = 0}^{\infty} \left( \frac{\left( -1 \right)^{k} \cdot \left( -a \right)^{2 \cdot k + 1}}{k! \cdot \left( 2 \cdot k + 1 \right)} \right)\\
&\quad \int_{-\infty}^{\infty} e^{-x^{2}} \operatorname{d}x = \lim_{a \to \infty} \left( \sum_{k = 0}^{\infty} \left( \frac{\left( -1 \right)^{k} \cdot a^{2 \cdot k + 1}}{k! \cdot \left( 2 \cdot k + 1 \right)} \right) - \sum_{k = 0}^{\infty} \left( \frac{\left( -1 \right)^{k} \cdot \left( -a \right)^{2 \cdot k + 1}}{k! \cdot \left( 2 \cdot k + 1 \right)} \right) \right)\\
&\quad \int_{-\infty}^{\infty} e^{-x^{2}} \operatorname{d}x = \lim_{a \to \infty} \left( \sum_{k = 0}^{\infty} \left( \frac{\left( -1 \right)^{k} \cdot a^{2 \cdot k + 1}}{k! \cdot \left( 2 \cdot k + 1 \right)} - \frac{\left( -1 \right)^{k} \cdot \left( -a \right)^{2 \cdot k + 1}}{k! \cdot \left( 2 \cdot k + 1 \right)} \right) \right)\\
&\quad \int_{-\infty}^{\infty} e^{-x^{2}} \operatorname{d}x = \lim_{a \to \infty} \left( \sum_{k = 0}^{\infty} \left( \frac{\left( -1 \right)^{k} \cdot a^{2 \cdot k + 1} - \left( -1 \right)^{k} \cdot \left( -a \right)^{2 \cdot k + 1}}{k! \cdot \left( 2 \cdot k + 1 \right)} \right) \right)\\
&\quad \int_{-\infty}^{\infty} e^{-x^{2}} \operatorname{d}x = \lim_{a \to \infty} \left( \sum_{k = 0}^{\infty} \left( \frac{\left( -1 \right)^{k} \cdot \left( a^{2 \cdot k + 1} - x\left( -a \right)^{2 \cdot k + 1} \right)}{k! \cdot \left( 2 \cdot k + 1 \right)} \right) \right)\\
&\quad \int_{-\infty}^{\infty} e^{-x^{2}} \operatorname{d}x = \sqrt[4]{6 \cdot \zeta\left( 2 \right)}\\
&\quad \int_{-\infty}^{\infty} e^{-x^{2}} \operatorname{d}x = \sqrt[4]{6 \cdot \frac{\pi^{2}}{6}}\\
&\quad \int_{-\infty}^{\infty} e^{-x^{2}} \operatorname{d}x = \sqrt[4]{\pi^{2}}\\
&\quad \int_{-\infty}^{\infty} e^{-x^{2}} \operatorname{d}x = \sqrt[2]{\pi}\\
&\quad \int_{-\infty}^{\infty} e^{-x^{2}} \operatorname{d}x = \sqrt{\pi}\\
\end{align*}

Woher ich das weiß: Studium / Ausbildung

Comments

[rixtwix007]

Der Lösungsweg Reihenentwicklung gefällt mir am besten. Jedoch verstehe ich es nicht mehr ab den Punkt Grenzen einsetzen. Kannst du ab da alles nochmal erklären? Das wäre supee

[LORDderANALYSE]

@rixtwix007

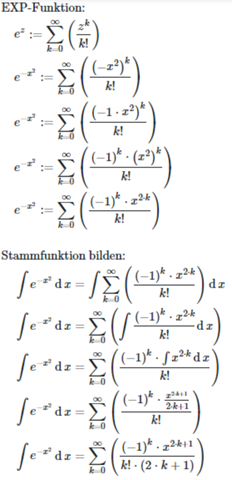
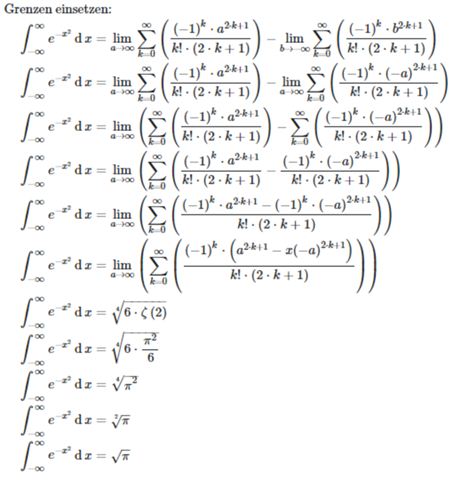
Legende

• Zeilennummer: Gemachter Schritt von der vorherigen Zeile zur aktuellen Zeile + Erklärung

Erklärung

• Zeile 2: Substitution der Limits (b := -a), womit im rechten Limit alle b zu -a werden. Da wir aber -a gegen -unendlich laufen lassen und "- * - = +" können wir das -unendlich im Limit durch ein unendlich austauschen und das Minus vor a weg lassen. Bildlich gesehen haben wir nun b durch a ersetzt und den Limit zu gegen unendlich gendert.
• Zeile 3: Wir fassen beide Limits zu einen zusammen, da in beiden der selbe Index a gegen etwas (unendlich) läuft.
• Zeile 4: Wir fassen die beiden Summen zu einer Summe zusammen. Summe (a_1 + a_2 + a_3 + ...) + Summe (b_1 + b_2 + b_3 + ...) ist selbst eine Summe (a_1 + a_2 + a_3 + ... + b_1 + b_2 + b_3 + ...), kann also als Summe ausgedrückt werden. Gemäß der Kommutativität bezüglich der Addition können wir die einzelnen Therme verschieben (a_1 + b_1 + a_2 + b_2 + a_3 + b_3 + ...), wobei wir die beiden n-ten Therme der Summe (a_n + b_n) zu einen neuen Therm zusammen fassen (c_n), wodurch wir eine Summe von den neuen Thermen erhalten (c_1 + c_2 + c_3 + ...), welche wir mit den Summenzeichen zusammenfassen können. Das Ergebnis ist die Zeile 4.
• Zeile 5: Wir schieben beides innerhalb der Summe auf einen Bruchstrich.
• Zeile 6: Wir klammern den (-1)-Therm aus.
• Zeile 7: Wir sehen, dass das ein Spezialfall der riemannschen Zeta Funktion ist und schreiben sie dementsprechend um.

[rixtwix007]

@LORDderANALYSE

Wir haben b als -a definiert, wieso wird es dann beim Limes zu a gegen unendlich und wieso bleibt es im Term bei -a?

[rixtwix007]

@LORDderANALYSE

Ich habe es nun verstanden, also Zeile.2: egal ob a oder -a gegen unendlich läuft, kommt das gleiche raus, wegen dem Minus vom -a.

Frage zu Zeile.7: welcher Spezialfall ist das, wo steht der?

Answer 2

[ChrisGE1267]

Entweder standardmässig durch Quadrierung des Integrals und Integration über die komplette Ebene durch Koordinatenwechsel zu Polarkoordinaten - da muss man aber schon etwas über die Funktionaldeterminante wissen.

Viel eleganter finde ich die Berechnung über Feynman‘s Trick:

https://medium.com/@rthvik.07/solving-the-gaussian-integral-using-the-feynman-integration-method-215cf3cd6236

Woher ich das weiß: Studium / Ausbildung – PhD Analytische & Algebraische Zahlentheorie

Answer 3

[mihisu]

Üblicherweise nutzt man da den Trick, das Quadrat des gesuchten Wertes zu berechnen, und diesen wiederum über eine Transformation zu Polarkoordinaten zu erhalten...

$\left(\int\limits_{-\infty}^{\infty}e^{-x^2}\,\text{d}x\right)^2$

$=\left(\int\limits_{-\infty}^{\infty}e^{-x^2}\,\text{d}x\right)\cdot \left(\int\limits_{-\infty}^{\infty}e^{-x^2}\,\text{d}x\right)$

$=\left(\int\limits_{-\infty}^{\infty}e^{-x^2}\,\text{d}x\right)\cdot \left(\int\limits_{-\infty}^{\infty}e^{-y^2}\,\text{d}y\right)$

$=\int\limits_{-\infty}^{\infty}\int\limits_{-\infty}^{\infty}e^{-x^2}\cdot e^{-y^2}\,\text{d}x\,\text{d}y$

$=\int\limits_{-\infty}^{\infty}\int\limits_{-\infty}^{\infty}e^{-\left(x^2+y^2\right)}\,\text{d}x\,\text{d}y$

[Transformation zu Polarkoordinaten (Genau genommen braucht man neben der Transformationsformel auch noch den Satz von Fubini.)]

$=\int\limits_{r=0}^{r=\infty}\int\limits_{\varphi=0}^{\varphi=2\pi}e^{-r^2}\cdot r\,\text{d}\varphi\,\text{d}r$

$=\int\limits_{r=0}^{r=\infty}e^{-r^2}\cdot r\cdot 2\pi\,\text{d}r$

$=-\pi\cdot \int\limits_{r=0}^{r=\infty}e^{-r^2}\cdot \left(-2r\right)\,\text{d}r$

$=-\pi\cdot \left(\underbrace{\lim\limits_{r\to \infty}e^{-r^2}}_{=0}-\underbrace{e^{-0^2}}_{=1}\right)$

$=-\pi\cdot \left(-1\right)$

$=\pi$

Und wenn man da nun die Quadratwurzel zieht, erhält man...

$\int\limits_{-\infty}^{\infty}e^{-x^2}\,\text{d}x=\sqrt{\pi}$

Answer 4

[Niemand18]

Du setzt J := int (e^(-x^2) dx) von -inf to inf und betrachtet J^2 = int(e^(-x^2)dx) * int(e^-(y^2) dy)

Jetzt Fubini und Substitution durch Polarkoordinaten verwenden.

Woher ich das weiß: Hobby – Selbststudium