Tangente durchläuft Punkte?
Aufgabe :
Gegeben ist die Funktion f mit f(x)=0,5x^2 Bestimme die Punkte des Graphen, dessen Tangenten durch den Punkt (1/0) verlaufen
3 Antworten
Es ist so gemeint:
Die Funktion f hat in jedem ihrer Punkte eine Tangente. Du sollst die Punkte herausfinden, deren Tangenten durch den Punkt (1|0) verlaufen. Würde der Punkt (1|0) beispielsweise auf der Symmetrieachse liegen, hättest du x_t und -x_t als Lösung.
Frage formuliert man so um
Tangente(n) von (1/0) an f(x)
yT = mx + b
P (px/py)
.
Die Tangentensteigung bekommt man aus der ersten Ableitung
f'(x) = 2*0.5x = x
.
einmal ist m =
0 - f(x) /(1-x)
einmal ist m = x
.
Gleichsetzen
0 - 0.5x²/(1-x) = x
0 -0.5x² = x - x²
0 = -0.5x² + x
0 = -x*(0.5x - 1)
bei x = 0 und bei x = +2 wird die Parabel berührt
.
.
Tangente 1 ist die x-Achse
.
Tangente 2 durch (2/2) und (1/0)
m = (2-0)/(2-1) = 2
.
0 = 2*1 + b
-2 = b
yT2 = 2x - 2
Probe im Bild
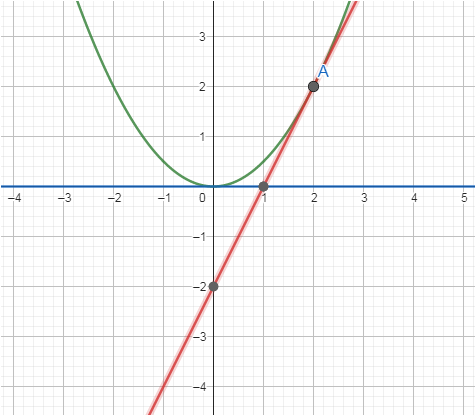
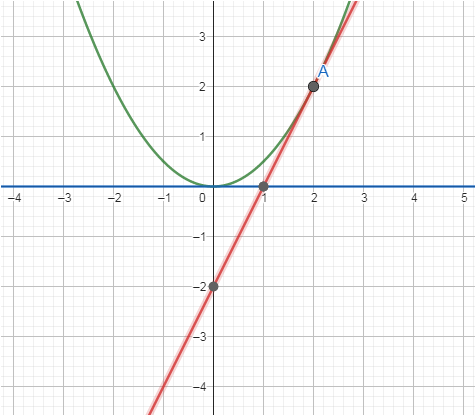
wenn man zwei Punkte hat , dann ist das die Formel für die Steigung einer Gerade zwischen ihnen ( Delta y durch Delta x ) . Egal ob die Gerade eine Sekante, Tangente , Passante oder "normal" ist .
Hier ist der eine Punkt in Zahlen bekannt (1/0) , der andere ist der Berührpunkt ( noch nicht in Zahlen bekannt ) . Deswegen steht da ( x / f(x) ) . Wobei f(x) eben durch 0.5x² ersetzt werden kann .
Man kann also auch eine Steigung als Formel angeben , ohne dass man schon die Zahlen kennt.
.
Eigentlich hätte ich auch unten wie oben (px/py) schreiben können , aber das war mir zu lang
.
der Gag bei dieser Frage ist eben der , dass man m auf zwei verschiedene Weisen formulieren kann : Als Ableitung und als Differenzenquotient , welche man dann gleichsetzt und so zum Ziel kommt.
Du musst en Gleichungssystem aufstellen:
1.) Punkt-Steigungsformel für die Tangente, die durch den Punkt (0/1) geht und die Steigung f'(x) hat.
2.) Die gesuchten Punkte liegen auf der Parabel, erfüllen also die Gleichung y=f(x)
{Lösung : P1=(0/0) undP2=(2/2)}
Die Steigung m =0 - f(x) /(1-x) hast du aber im dem Fall mit dem Differenzenqutionteten berechnet oder ,das ist doch der Durchschnitt sozusagen. Das benutzt man doch um sekanten zu berechnen oder?