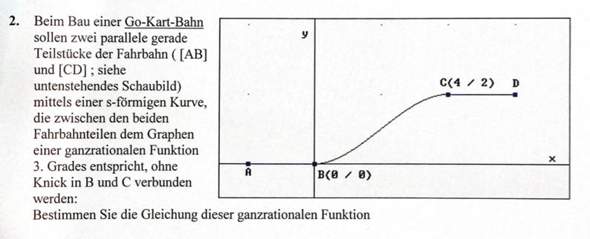
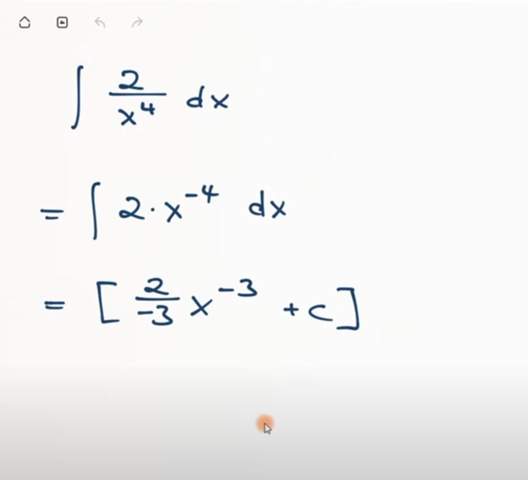
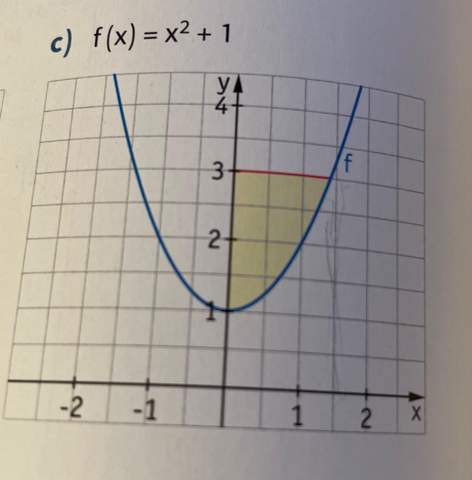
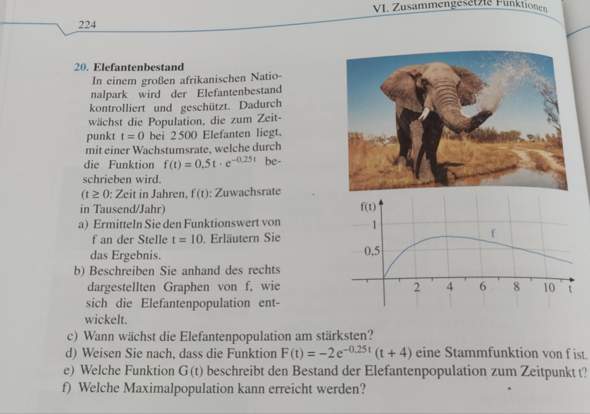
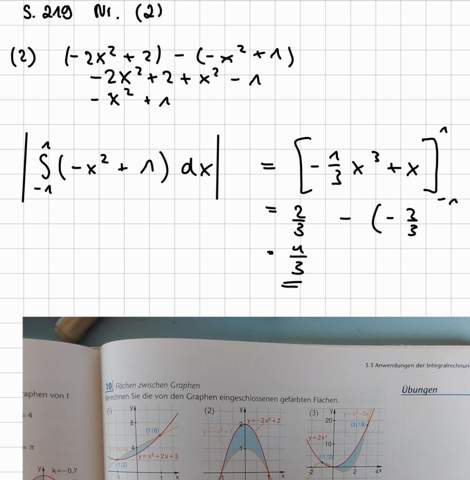
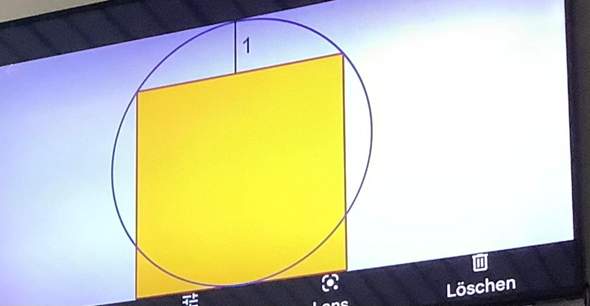
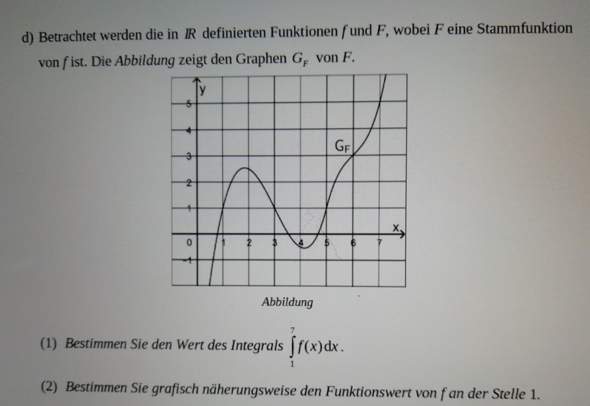
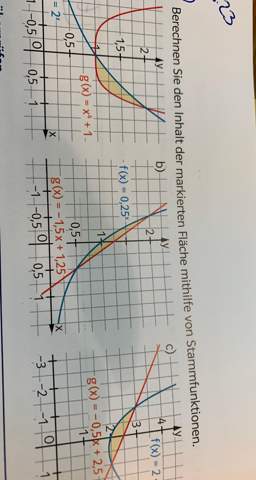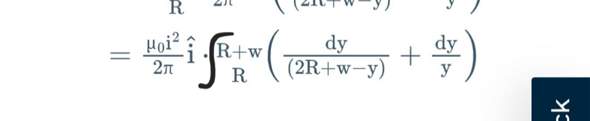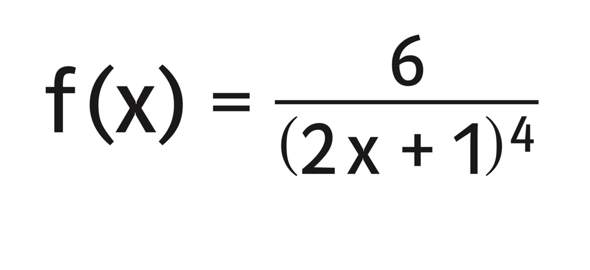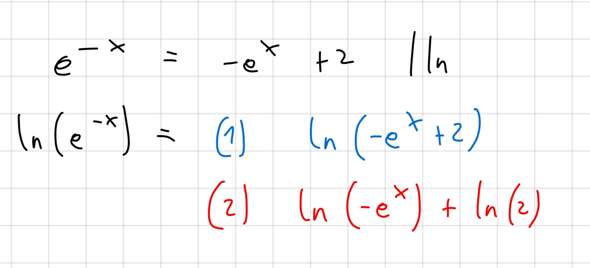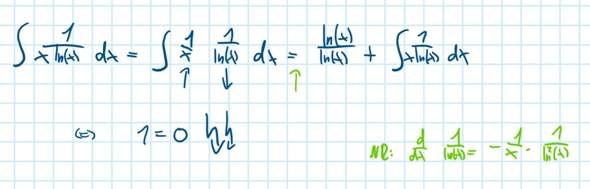Zu der Aufgabe wäre das meine Lösung:
a) Um die Extrema und Wendepunkte der Funktion f(x) = e^x - x zu bestimmen, betrachten wir zuerst die Ableitung f'(x). Setzen wir f'(x) = 0, um mögliche Extremstellen zu finden:
f'(x) = e^x - 1 = 0
Daraus folgt:
e^x = 1
Da die Exponentialfunktion e^x niemals negativ wird, kann sie nur an einer Stelle den Wert 1 erreichen, und das ist bei x = 0 der Fall. Somit haben wir eine Extremstelle bei x = 0.
Um festzustellen, ob es sich um ein Minimum oder Maximum handelt, betrachten wir die zweite Ableitung f''(x):
f''(x) = e^x
Da f''(0) = e^0 = 1 positiv ist, handelt es sich bei x = 0 um ein Minimum.
Da wir kein weiteres Extremum gefunden haben und die Funktion f(x) nach oben offen ist, besitzt sie keine weiteren Extrema oder Wendepunkte.
b) Da f(0) = 1 und es keine weiteren Extremstellen gibt, gibt es keine kleineren Werte als 1 auf dem Funktionsgraphen. Daher hat die Funktion f(x) keine Nullstellen.
c) Um zu zeigen, dass der Zubringer tangential in die Autobahn mündet, müssen wir den Anstieg der Funktion f(x) an der Stelle x = 1 mit dem Anstieg der Geraden des Zubringers vergleichen.
Der Zubringer wird durch eine Geradengleichung y = ax + b beschrieben. Da der Punkt (0,0) auf der Geraden liegt, ist b = 0. Der Punkt (1, f(1)) = (1, e^1 - 1) liegt ebenfalls auf der Geraden, daher setzen wir ihn ein:
f(1) = e^1 - 1 = e - 1
Daraus ergibt sich:
f(1) = a*1 + b = e - 1
Da b = 0, erhalten wir a = e - 1.
Somit hat die Gerade des Zubringers die Gleichung y = (e - 1)x.
Der Anstieg der Funktion f(x) an der Stelle x = 1 ist gegeben durch f'(1) = e^1 - 1 = e - 1.
Der Anstieg der Geraden des Zubringers ist ebenfalls e - 1.
Da beide Anstiege gleich sind, mündet der Zubringer tangential in die Autobahn.
d) Um die Fläche des Grundstücks zwischen Straße, Zubringer und Bahnlinie zu berechnen, müssen wir den Bereich zwischen den entsprechenden Kurven auf dem Graphen bestimmen.
Die Straße wird durch die x-Achse (y = 0) dargestellt.
Die Gerade des Zubringers ist y = (e - 1)x.
Die Bahnlinie wird durch die Gerade y = x dargestellt.
Wir müssen nun die Schnittpunkte dieser Kurven finden:
0 = (e - 1)x
x = 0 (Schnittpunkt bei B)
und
x = 1 (Schnittpunkt mit der Autobahn)
Der Bereich zwischen den Kurven erstreckt sich also von x = 0 bis x = 1.
Um die Fläche dieses Bereichs zu berechnen, verwenden wir das Integral. Da die Kurvenfunktionen y = (e - 1)x und y = x den Bereich begrenzen, integrieren wir die Differenz der beiden Funktionen von x = 0 bis x = 1:
Fläche = ∫[0,1] [(e - 1)x - x] dx
Die Berechnung des Integrals ergibt:
Fläche = [((e - 1)x^2)/2 - (x^2)/2] |[0,1]
= ((e - 1)/2 - 1/2) - (0/2 - 0/2)
= (e - 2)/2
Da 1 Hektar 10,000 m² entspricht, können wir die Fläche in Hektar umrechnen:
Fläche = (e - 2)/2 * 10,000 m²
Somit hat das Grundstück zwischen Straße, Zubringer und Bahnlinie eine Fläche von (e - 2)/2 * 10,000 m² bzw. (e - 2)/2 Hektar.