Integral näherungsweise mit Produktsummen berechnen?

Hallo,

ich brauche Hilfe bei einer Aufgabe zu Integralen. Die Aufgabe lautet: "Berechnen Sie das Integral näherungsweise mithilfe von Produktsummen."
Das Integral von f(x)= (2-x)^2 von 0 bis 4 ist gegeben.

Ich habe für Delta x= 4/n und als Intervallgrenzen

0, 2* 4/n, 3*4/n,..., (n-1)*4/n und dann

Sn (Produktsumme) = 4/n * (4+(8/n-2)^2 + (12/n-2)^2 + ... + (4n-4/n -2)^2)

aber ich komme leider nicht weiter und ich verstehe nicht wie ich auf ein Ergebnis komme.

Es wäre sehr nett, wenn sich jemand die Zeit nehmen könnte, um mir zu helfen!
Vielen Dank im Voraus.

Answer 1

[evtldocha]

Ich weiß offen gesagt nicht genau, was ihr im Unterricht zu dem Thema gemacht habt - ich jedenfalls würde das so rechnen:

$S_n=\sum_{k=1}^nΔx\cdot f\left(Δx\cdot k\right)=\frac{4}{n}\cdot\sum_{k=1}^n\left(2-\frac{4}{n}\cdot k\right)^{^2}$

Nun in der Summe die Binomische Formel anwenden und die Summe in 3 Teilsummen aufspalten. Anschließend alles mit den Formeln

$\sum_{k=1}^n4=4n;\ \sum_{k=1}^nk=\frac{n\cdot\left(n+1\right)}{2};\ \ \sum_{k=1}^nk^2=\frac{1}{6}n\cdot\left(n+1\right)\cdot\left(2n+1\right)$ zusammenfassen. Das liefert nach einer etwas längeren Rechnerei:

$S_n=16-\frac{64\cdot\left(n+1\right)}{6n}\cdot\left(1-\frac{1}{n}\right)$

oder noch einfacher:

$S_n=16-\frac{64}{6}\cdot\left(1-\frac{1}{n^2}\right)$

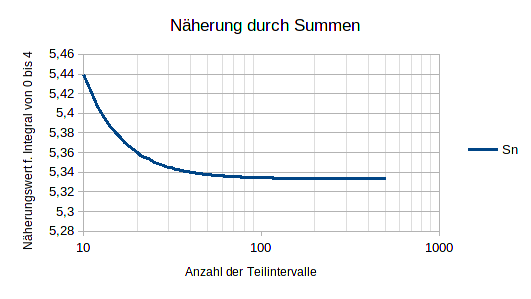
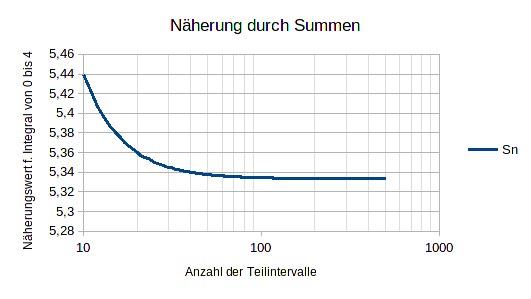
Jetzt kannst Du einen beliebigen Wert "n" einsetzen um eine Näherung für die (Ober-)Summe zu erhalten. Da die Summe sehr langsam konvergiert wird das Ergebnis erst ab n=100 einigermaßen an den exakten Integralwert von 16/3 heranreichen.