Wie kann man die Wasservolumen berechnen?
Die Aufgabe lautet: Im Sommer steht das Wasser im Kanal an der tiefsten Stelle 1 Meter hoch. Bestimmen Sie das Wasservolumen des beschriebenen Kanals im Sommer.
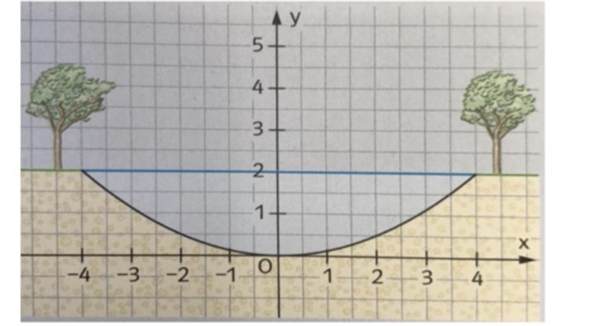
f(x)= 1/8x²
Ich habe den x Wert für y=1 berechnet, also 2√2 und dann subtrahiert mit Integrale der Querschnittsflächen in gelb 1,885618 was dann subtrahiert 0,94280 ergab.Dann habe ich V = G* h = 0,94280m²* 1000m = 942,8m³ raus, aber es stimmt nicht mit den Lösungen überrein. In der Lösung heißt es 3770 m³. Könnt ihr mir helfen?
Der Kanal ist 1km lang.
2 Antworten
Hallo,
die Lösung ist falsch.
Das Integral über ((1/8)x²-2)dx in den Grenzen von -4 bis 4 hat den Betrag von 32/3 m², wenn eine Flächeneinheit ein Meter sein soll.
Das mal 1000 ergibt 32000/3=10666,67 m³ Volumen.
Herzliche Grüße,
Willy
Jetzt sehe ich es. Im Sommer hast Du einen Wasserstand von 1 m. Dann mußt Du von - Wurzel (8 ) bis Wurzel (8) rechnen über (1/8)x²-1. Dann sind es 3771,236 m³.
Jap, auf das selbe komme ich auch. @wagmaw ich könnte dir meinen rechenweg schicken?
Also ich habe beim Integral= 1,88561808 raus. Bei meiner Rechtecksfläche habe ich Wurzel 8 raus. Das beides subtrahieren 1,88561808-Wurzel 8 = 0,9428090447. Danach die Volumenformel V= 0,9428090447m^2 * 1000m = 942,8090447m^3, stimmt immer noch nicht,,,
Du musst die Wurzel 8- das integral rechnen. (Rechteck minus Fläche unter dem Graphen= Fläche über dem Graphen)
Anders herum hättest du den selben wert negativ raus. Da kannst du aber den Betrag nehmen.
du musst ZWEI mal Wurzel 8 nehmen.
aber ich muss doch die 1m berücksichtigen oder? demnach muss man ab die 1m ein rechteck konstruieren und berechnen, und die neuen x Grenzen ergeben dann 2wurzel 2 und -2wurzel 2. Und demnach auch die integralgrenzen...
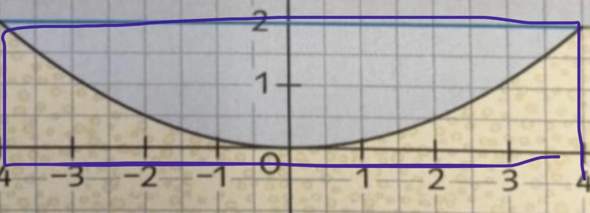
Das da kann man als Rechteck betrachten mit dem Flächeninhalt 8*2=16
dann integrierst du deine Funktion von -4 bis 4.
ein integral ist die Fläche unter einem Graphen. Im also die Fläche über dem Graphen zu bekommen (das Wasser), rechnest du 16-Integral von -4 bis 4
(Rechteck minus integral)
ich habe vergessen dazuzuschreiben, dass der Kanal 1km lang ist.
Die Aufgabe lautet: Im Sommer steht das Wasser im Kanal an der tiefsten Stelle 1m hoch. Bestimmen Sie das Wasservolumen des beschriebenen Kanals im Sommer.
mein Fehler. Ich hab die Aufgabenstellung überlesen. Ja du schaust was bei y=1 rauskommt, da müsste 2x der selbe wert raus kommen, einmal positiv und einmal negativ. Das sind deine integralgrenzen. Das mit dem Rechteck kannst du genauso machen, nur der Flächeninhalt ist ein anderer. (Wenn das mit dem 2Wurzel 2 stimmt dann 2Wurzel2-(-2Wurzel2)
Also meine Grenzen für mein Integral waren ja auch 2wurzel2 und -2wurzel 2... aber ich weiß nicht, wieso ich nicht das richtige ergebnis bekomme
es geht nicht um die Grenzen von -4 bis 4. ich habe die Aufgabenstellung erst auch nicht gelesen ;)