wenn hier 3 variablen unbekannt sind, geht das ja nicht....

Hallo, ich hänge hier bei einer Mathe Aufgabe, bei dem Thema hab ich etwas Schwierigkeiten. um eine Basis zu bestimmen muss man schauen ob alle Mengen linear unabhängig voneinander sind und ob durch Linearkombination aus Teilraum T der Vektor M erzeugt werden kann. Wie kann ich dann nur einen aussuchen wenn alle M als Ganzes da steht und nicht als einzelne? Oder verstehe ich hier etwas nicht richtig? Ich bin dankbar für jeden Lösungsvorschlag!

Es heißt:

,,Berechnen Sie die Lösung des linearen Gleichungssystems´´:

0,5x - 3y = 7,5

6x + 5y = 8

Vielen Dank für eure Mühe:)

Es gibt ja die Formel f(x)=k*x+d

Aber was ist was?
Beispiel:
Eine 40cm große Kerze brennt gleichmäßig ab. Nach 10 Stunden ist sie noch 27cm hoch.

1. Ermittle die Funktion, die die Höhe der Kerze nach der Brenndauer t (in Stunden) angibt.
2. Wie lang brennt die Kerze?

Ich habe jetzt 3 Angaben (40cm, 10 Stunden, 27cm), aber wo setzte ich was ein? Und ist das immer gleich?

Bei mir kommt irgendwie ein falsches Ergebnis raus und bei den Lösungen steht kein Rechenweg. Kann jemand die a lösen (mit Rechenweg )damit ich das nachvollziehen kann.

Danke

Hallo, also am Freitag schreibe ich einen Test in Mathe es sind lineare Gleichungen und all das was dazu gehört. Und ja ich bin nicht die hellste Kerze in Mathe aber dieses Thema verstehe ich wirklich garnicht egal was ich mach ich hab mir schon unzählige Videos angesehen und meine Lehrerin gefargt und meinen Eltern aber irgendwie hilft nichts. Nur leider kann ich nicht sagen das ich das nicht verstehe um den Test nicht zu schreiben. Was soll ich jetzt machen?

Würde mich auf Antworten freuen!

Hallo,

ich habe zurzeit ein Problem mit einer Matheaufgabe. Wir müssen bei dieser den Gauß-Algorithmus anwenden, jedoch finde ich keinen Ansatz. Ich würde mich über hilfe freuen.

Danke im Voraus!

Es geht um das Gaus verfahren und das dreieckssystem.

danke

Nur die Nummer 1

Nur bei der a)

Bei der a) habe ich 4 und 6 raus bin aber nicht sicher

Hallo! Ich bräuchte Hilfe bei meinen Physik aufgaben! Die sind eigentlich bis Mittwoch, wollte sie aber jetzt schon erledigen, und sitze hier jetzt schon so lange, verstehe es aber immernoch nicht😞 Aufgabe 2 :)

1a und c

2x1 - 4x2 - x3=1

5x2 + 2x; = 16

3x3 = 9

Hallo, könnt ihr mir bitte helfen?

das Thema ist Lösungsmengen linearer Gleichungssysteme ( Gauß verfahren)und ich verstehe es nicht. Ich werde mich auf Ihre Antwort freuen!

Hallo,

ich habe eine Frage bezüglich dieser Aufgabe und zwar wie geht man hier genau vor und wie kann ich dem Gleichungssystem Informationen entnehmen, sodass sie mir helfen, die Abbildungen zuzuordnen?
Freue mich über jede Antwort

MfG

Hallo,

Ich habe Mathe Hausaufgaben und verstehe

1. Die Nummer sechs nicht ganz, bzw wo da mein Fehler liegt

Und bin mir

2. Unsicher, ob ich die Nummer elf richtig verstanden habe.

Ich habe versucht, alles übersichtlich zu halten, damit schlüssig ist, wie ich gerechnet habe.

Ich freue mich auf euer Hilfe

(Bilder werden sofort angefügt)

Moin!

brauche gerade Hilfe bei meinen Hausaufgaben weil ich nicht weiß wie ich das zweite Zahlenspiel herausfinden kann. Wenn mir jemand das erklären könnte wäre das super :)

(Nr. 4)

Wie gibt man bei einer Gleichung eine Unendliche Lösungsmege an ? Gibt es eine bestimmte Formel ? Und wie wäre die unendliche lösungsmenge im diesem Beispiel ? :

Hallo,

Ich schreibe demnächst eine Arbeit und wollte wissen, wie ich bei Nummer 2 vorgehen muss.

Hi,

schreibe in ein paar Tagen Mathe und bin mega Safe in dem Thema, es fällt mir wirklich leicht und ich kann auch fast alle sachaufgaben lösen oder finde direkt einen Ansatz. Das Problem ist jedoch, wie löse ich diese sachaufgaben mit Linearen Gleichungssystemen ? Also sprich, nicht das Berechnen das kann ich, aber wir stelle ich hierzu das LGS auf ? Ich finde die LGS erstmal aufzustellen ist viel schwerer als das zu berechnen

Es gibt zwei geraden wo con der geradenbüschel berechnet werden soll.

5= a+b

8= a+2b

11=a+3b

Wie stelle ich davon jetzt die Maschengleichungen auf bzw. das LGS?

30x - 15y = 9

-15x + 45y - 15z = 9

-15y + 30z = 9

Oder wie?

Guten Tag,

bei meiner Frage geht es um das Aufstellen von Funktionsgleichungen mit linearen Gleichungssystemen. Es gilt, alle ganzrationale Funktionen vom Grad zwei zu bestimmen, deren Graphen durch die Punkte A(2|0) und B(-2|0) verläuft.

Ich habe bisher ein lineares Gleichungssystem anhand der allgemeinen Funktionsgleichung f(x) = ax² + c erstellt, da die Parabel ja achsensymmetrisch ist. Dieses Gleichungssystem hat jedoch unendlich viele Lösungen (eine Zeile nur mit Nullen) und ich weiß nicht, wie ich jetzt weiter verfahren muss. Ich dachte, ich könnte eine Funktionsschar aufstellen, jedoch weiß ich nicht, wie das in diesem Fall funktioniert. Ich weiß somit nicht, wie ich die Lösung zu dieser Aufgabe angebe.

Ich würde mich über jede Hilfe freuen. Danke im Voraus!

Hey, ich sehe nicht wo der Fehler in beiden Gleichungen ist. Ich habe alles Schritt für Schritt nachgerechnet und die Lösung macht sogar Sinn wenn man Sie einsetzt:

Hat jemand eine Idee?

Vielen Dank!

Hallo,

mich wollte fragen ob ich dies auch als Limes schreiben könnte ,und wenn wie?

Ich habe eine Mathefrage: Stell dir ein Rechteck vor. Die 2 Seiten Länge zusammen müssen 11 m lang sein. Wie lang sind die Seiten das der höchste Flächeninhalt entsteht

Ich habe links das Gleichsetzungsverfahren gemacht, da habe ich keine Fragen zu, alles in Ordnug.

ich habe zwei unterschiedliche Verfahren benutzt.

rechtsseitig ist das gaussche Eliminationsverfahren, ein überbestimmtes LGS, wobei zwei Gleichungen redundant sind. Aus einer Zeile entsteht 0=0, das sagt, dass beide Geraden aufeinander liegen. Was bedeutet das nun, wenn die andere Gleichung 0=6 ist, dies bedeutet doch es gibt keine Lösung, weil das eine nicht wahre Aussage ist, also sind sie parallel zueinande. Ich verstehe jetzt nicht, wie ich welchen Schluss ziehen kann. Liegen die Geraden nun aufeinander oder sind die parallel zueinander, nach dem gausschen Algorithmus? (Ich habe das Vertauschen beider Zeilen sein lassen und es im Kopf gemacht)

hallo,

wir befassen uns um Unterricht gerade mit Sachaufgaben zu linearen Gleichungssystemen und so ganz einfache lgs in sachaufgaben kann ich problemlos aufstellen genauso wie auch bei “etwas” schwierigeren Aufgaben. Aber bei den hier zum Beispiel (vor allem bei 6) habe ich keinen Plan wie man das aufstellen soll, da die 6 hier sogar physikalisch nicht mal Sinn macht (?). Kann mir jemand erklären wie man in solchen Aufgaben wie auf der Seite die Gleichungssysteme einfach aufstellen kann ? Das berechnen ist wiederum kein Problem für mich

Wie geht man an sowas ran um es zu lösen mit dem < Zeichen?

Ich habe mir überlegt ob ein überstumpfwinkliger Winkel(über 181 grad) in einem Dreieck seien kann weil die Summe der Winkel von einem Dreieck ja immer 180° ergeben also habe ich es mir auf ein Blatt Papier aufgezeichnet und es ging aber in google steht überall das dass nicht möglich währe wüsste ihr vielleicht ob das überhaupt seien kann und wieso die Summe über 180° ergibt

Danke im voraus!

Hallo liebe Community,

Ich werde demnächst eine GFS (ein Referat) in Mathe zum Thema "Mischungen" bzw. das Gauß-Verfahren halten.

Ich würde gerne ein paar Beispiele aus dem Alltag nennen, bei denen man das Gauß-Verfahren auch anwenden kann, kennt ihr welche?

Sie müssen nicht spezifisch sein, sondern eher allgemein, wie z.B. "in der Ernährung zur Berechnung von 3 Nährstoffen in 3 Lebensmitteln."

Schöne Woche noch ;)

Hallo zusammen,

ich habe im September ein Studium in Informatik begonnen. Pflichtveranstaltungen sind dabei Analysis 1 und Lineare Algebra 1. Ich bin aber gerade echt am Verzweifeln. Im Gymnasium war ich echt gut in Mathe, aber in diesen zwei Fächern weiss ich einfach nicht wie ich z.B. die Aufgaben lösen soll (wie man da vorgeht, Gedankenschritte, etc.). Habt ihr evtl. eine Empfehlung wie man sich gut für die Klausur vorbereiten kann? Lehrbücher, welche einfach zu verstehen sind und wirklich von 0 anfangen zu erklären?

ich wäre echt um jede Hilfe und Unterstüzung dankbar, denn ich weiss momentan echt nicht weiter...

Danke schon mal!

PS: bitte sagt mir nicht, ich solle direkt aufhören - ich will es wirklich versuchen.

Ich habe zwei Aufgaben, verstehe das Thema aber noch nicht ganz.

Bei den Lösungen steht, dass bei der 1. Aufgabe die Gleichung keine Lösung hat und bei der 2. Aufgabe, dass die Gleichung für jedes x lösbar ist, aber warum? Bei der 1. und 2. Aufgabe fallen die x-Werte komplett weg.

Wie löst man das folgende lineare Gleichungssystem mit dem gaußschen Algorithmus, sodass eine Zeilenstufenform entsteht?

Hallo,

ich brauche Hilfe bei dieser Aufgabe :

Zwei unterschiedlich lange Kerzen wurden gleichzeitig angezündet. Nach zwei Stunden hatten beide Kerzen die gleiche Länge. Die eine Kerze war nach insgesamt dreieinhalb Stunden ganz abgebrannt, die andere nach insgesamt fünf Stunden. Um wie viel Prozent war eine Kerze zu Beginn länger als die andere?

ICH MUSS DABEI BESTIMMMEN WOFÜR X UND Y STEHEN UND ZWEI LINEARE GLEICHUNGEN AUFSTELLEN.

LG

Hallo,

ich brauche nur Hilfe bei der Aufstellung des Gleichungssystems. Was bedeutet das Stimmenverhältnis der gültigen Stimmen war 5:4 :

Bei der Stichwahl für das Amt der Bürgermeisterin siegt Frau Schwab mit einer Mehrheit von 1236 Stimmen gegenüber Frau Beyer. Das Stimmenverhältnis der gültigen Stimmen war 5 : 4.

Danke für die Hilfe

Ich weiß einfach nicht weiter, wenn jemand vor mit Gleichungen löst finde ich es verständlich und plausibel, aber selber so vorrangen kann ich einfach nicht.

Wie löst man diese Gleichungen?

Hallo, kann jemand diese Aufgabe lösen?

Herr Krause hat testamentarisch festgelegt, dass seine beiden Kinder nach seinem Tod je 1/3 seines Vermögens erhalten. Der verbleibende Betrag wird auf die 5 Enkel verteilt. Jeder Enkel erhält nach diesen Bestimmungen 1.500€. Wie groß das das Vermögen von Herr Krause

Hallo,

Wie zeichnet man dass? Auf dem Koordinaten System.

LG

Hallo, ich muss in Mathe Grundkurs eine GFS machen und unsere Lehrerin hat uns Themen zur Auswahl gegeben, die in Stufe 12 und 13 behandelt werden (Berufliches Gymnasium). Welche(s) dieser Themen ist am einfachsten? Wir sollen darüber dann eine Unterrichtsstunde und Ausarbeitung gestalten danke :)

Danke für jede Hilfe!

Hi, wie löse ich die Aufgabe? ich habe bei der a)

” 8über 2” = 28?

stimmt das?

bei b) habe ich “5000 über 2” = 12.497.500

stimmt das ?

C habe ich : “25 über 3” = 2300

stimmt das so? was habe ich falsch gemacht?

Wie kann ich wissen ob ich das Gleichsetzungsverfahren oder das Einsetzungsverfahren benutzen soll? Kann jemand bitte es mit Zusammenhang der Aufgabe 9 erklären. Danke

Könnt ihr mir bitte bei der Gauß‘sches Eliminationsverfahren helfen. Wir haben das Thema in der Stunde nie behandelt. Haben die Aufgabe als Lernauftrag aufbekommen. Habe mir Dutzende Videos angeschaut aber kann irgendwie diese Aufgabe nicht lösen. Wäre super nett wenn ihr helfen könnt bzw. Auch erklären könnt. Damit ich das auch verstehe und in den anderen Aufgaben anwenden kann. Danke :)

aufgabe:

4x-2y+2z=2 

-2x+3y-2z=0

3x-5y+ z=-7

2y = -6 +6y-2

Also

2y = -6 +6y-2 | : 2

y = -3 +3y -1

Ich soll ein paar Gleichungen nach y auflösen und habe null plan

Beispiel:

I 2x+y=8

II 4x-y=10

Woher weiß ich, welches Verfahren ich einsetzen muss, wenn es zwei Variablen in einer Gleichung gibt? Es gibt das Gleichsetzung und das Einsetzungsverfahren.

Gibt es ein Dreieck mit folgenden Eigenschaften? Ein Winkel ist das Doppelte eines anderen Winkels. Die beiden Winkel sind zusammen 36° größer als der dritte Winkel.

Die St.-Georg-Sprungschanze in Winterberg im Sauerland wurde im Jahr 2000 zu einer Ganzjahresanlage umgebaut. Man kann ein Koordinatensystem mit dem Ursprung O senkrecht unter dem Schanzentisch am Beginn des Aufsprunghügels zugrunde legen.

Folgende Maße (in Meter) sind dann für die Winterberger Schanze bekannt:

Der Wendepunkt K hat die Koordinaten (-69,6 |-38,6), die maximale Steigung beträgt 35,5°.

Die x-Koordinate des Hillsize-Punktes H beträgt - 74,6.

1. Ermitteln Sie eine ganzrationale Funktion dritten Grades, deren Graph das Profil des Aufsprungbereichs zwischen dem Hillsize-Punkt H und dem kritischen Punkt K beschreibt.
2. Begründen Sie, dass die in Teilaufgabe a) gefundene Funktion nicht geeignet ist, das Profil des gesamten Aufsprunghügels zu beschreiben.

Wie geht man vor? Was sind die Bedingungen und wie kommt man auf die?

Hallo, könnte mir jemand bei dieser Aufgabe eventuell weiterhelfen?
Normalerweise nutzt man hierbei ja das Gauß-Verfahren, aber das ist hier ziemlich kompliziert umzusetzen. Daher könnte mir jemand eventuell helfen?

Danke und liebe Grüße :)

Ich brauche Hilfe bei der Lösung dieses Mathe Aufgabe!!

Eine Jugendgruppe benötigt für einen Theaterbesuch 11 Karten. Sie bekommt jedoch nur noch 4 Karten in der teuren Preisklasse und 7 in der 3€ billigeren Preisklasse. Zusammen kosten die Karten 100€.

Wie teuer sind die Karten in den beiden Preisklassen?

Wie berechne ich das?

Als Lösung habe ich AB ist 13,1 m

ich habe Schwierigkeiten mit Textaufgaben. Wie löse ich a und b? Kann jemand helfen?

Warum muss ich hier die Vorzeichen ändern?

Also Quadratische Gleichungen kann ich easy Rechnen aber bei eine Textaufgabe bin ich komplett auf null. Textaufgaben sind ja meistens das Problem in Mathe aber bei diesem Thema ist dass noch mal eine extra Wurst

Hier wären ein paar meiner Textaufgaben könnt ihr mir irgendwie helfen in diesem Thema die Textaufgaben zu verstehen

Für mich ergibt sich der Sinn nicht. A ist eine Matrix. sigma_i ein Skalar. u_i ein Spaltenvektor und v_i^T ein Zeilenvektor. Laut Skalarprodukt ergibt alles was in der Summe steht am Ende eine Zahl und keine Matrix.

Hallo,

ich bräuchte ganz dringend Hilfe!
Ich übe gerade für meine Klausur und schaue mir unterbestimmte lineares Gleichungssystem an. Das Problem ist, dass ich versucht habe das lineare Gleichungssystem zu lösen, aber leider kommt bei mir ein falsches Ergebnis raus und ich verstehe leider garnicht, was mein Fehler ist.

Könnte mir jemand dabei helfen?

Hallo ihr Lieben,

meine Lerngruppe und ich stolpern über diese Übungsaufgabe. Wir sollen die Lösungen des LGS bestimmen und können keinen richtigen Anfang finden. Vielleicht hat einer von euch eine Idee?

LG :)

Wie berechnet man diese

Gleichung mit dem

Gleichsetzungsverfahren?

Bei mir kommen andere Zahlen raus die nicht überein stimmen (Lösungen).

Bei der unten angehängten Aufgabe komme ich nicht weiter. Ich habe die Lösung dazu aber weiss nicht wie man zu dieser kommt.

Lösung: grösserer Kredit in CHF -> x =14400

kleinerer Kredit in CHF -> y = 10800

Ich brauche Hilfe bei diesen Aufgaben:

1) Bstimmen Sie eine ganzrationale Funktion 5.Grades, deren Graph zum Koordinatenusrsprung symmetrisch ist und für die gilt: Der Graph hat eine Nullstelle mit waaderechter Tangente bei X=1, im Ursprung beträgt die Steigung 1.

2)Bestimmen Sie eine ganzrationale Funktion möglichst niedrigen Grades mit folgenden Eigenschaften:

1. T(0|0] ist Tiefpunkt des Graphen und W (1 | 11) ist Wendepunkt.
2. S(0|3] ist Sattelpunkt des Graphen. Ferner liegt im Punkt P (3|0) eine waagerechte Tangente vor.
3. Der Graph hat den Wendepunkt W (0|1) und berührt die Parabel mit der Gleichung g(x) = x? + x in ihrem Scheitelpunkt.

3)Von einer ganzrationalen Funktion f 4.Grades sind folgende Bedingungen bekannt:

1. f[2)=4
2. f(2)=0
3. f(0)=0
4. f"(0) = 0
5. f(0)=1

Entscheiden Sie, ob die von David und Anna formulierten Aufgaben zu den gegebenen Bedingungen passen. Überprüfen Sie anschließend, ob die Aufgaben lösbar sind.

David: T(2 | 4) ist Tiefpunkt des Graphen von f, W(0 | 0) ist Wendepunkt der Steigung 1.

Anna: „Der Graph der Funktion f hat im Koordinatenursprung einen Wendepunkt. Die Wendetangente hat die Gleichung y = x.Im Punkt P(2 | 4) hat der Graph eine waagerechte Tangente."

Hallo,

Ich bin gerade dabei den Gauß Algorithmus zu üben und komme bei dieser Gleichung nicht weiter… als x muss nämlich eigentlich 1 rauskommen , bei mir kommt aber stattdessen 53 raus…

Sieht jemand von euch den Fehler ?

Wäre sehr dankbar , wenn jemand darüber schauen könnte :)

Kann mir vielleicht jemand den reihenweise erklären?

Ich weiß einfach nicht wie ich auf die Grundgebühr kommen soll...

Ich komme irgendwie immer bis zum Gleichungssystem kann dieses allerdings nie korrekt lösen . (Die Aufgaben sind vom selben Arbeitsblatt wie in der ersten Frage . 😭)

Hat jemand einen Lösungsansatz für mich? Fangen das Thema gerade erst neu an und sehe keine Möglichkeit LGS etc anzuwenden.

Hallo,

es geht um folgende Aufgabe:

Es soll ein LGS mit drei Gleichungen und drei Variablen aufgestellt werden, das die angegebene Lösungsmenge hat. Die Koeffizienten sollen ungleich null sein.

Die Lösungsmenge ist: L={(5;t;t+1)}.

Bisher habe ich es immer so gemacht, dass ich beim Lösen eines LGS mit unendlicher Lösungsmenge für x3 in der dritten Zeile immer t gewählt habe, weshalb es mich schon verwirrt, dass bei x2 die Variable t steht. Ich komme bisher einfach nicht dahinter, wie man diese Art von Aufgabe richtig löst, möchte es aber unbedingt verstehen.

Ich würde mich über eine ausführlichere Antwort freuen, die sich auch genau auf diese Aufgabe bezieht.

Vielen Dank schon mal!! :))

Hallo, ich habe eine Aufgabe, in der ich ein Gleichungssystem zu lösen habe mit 4 Gleichungen und 3 Unbekannten, leider komme ich hier mit Hilfe des Gaußschen Algorithmusses nicht weiter und wollte um Hilfe fragen. Unten seht ihr das Bild zu meiner Aufgabe.

Wie löst man dieses Gleichungssystem?

Irgendwie ist alles, was ich versuche falsch. Ich benutze hier den Gauß-Algorithmus.

Gesucht ist die Funktion zu den oben gegebenen Bedingungen. Ich habe da raus, dass das nicht geht, aber das scheint mir falsch, weil ich so eine Funktion ja ziehen kann.

Hallo Zusammen

Wie löse ich die Aufgabe 3b?

Lg. und danke im Voraus :)

Hallo,

ich habe eine Matheaufgaben bekommen. Die Aufgabe lautet wie folgt: Bestimme die Variablen a, b, c und d der Funktion ax^3+bx^2+cx+d so, dass die Funktion durch die Punkte A(-4|-2), B(-2|2) und C(4|-4) verläuft und die Steigung an der Stelle 4 = 1 beträgt.
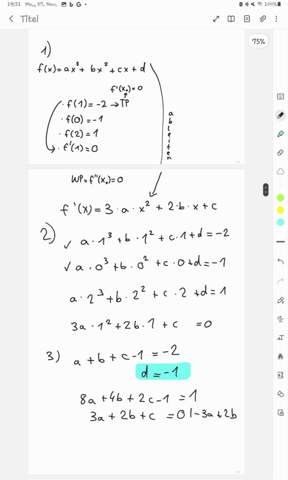
Also habe ich die Punkte in die Funktion eingesetzt, vereinfacht was zu vereinfachen war, ein LGS erstellt, die Matrix meines Taschenrechners bedient und 4 Werte rausbekommen (rechts; unter „Matrix“):

Soweit passt alles - dachte ich zumindest. Habe die Bedingungen mit GeoGebra überprüft, indem ich eine Tangente an dem x-Wert 4 erstellt habe und die Steigung abgelesen habe. Und siehe da, die Steigung ist nicht, wie sie sein sollte. Anstatt 1x liegt sie bei 0,5x:

Meine Frage ist nun, ob das vielleicht die „Herausforderung“ der Aufgabe ist, dass dieses Problem auftreten soll, oder ob ich einen dicken Denkfehler habe?

Vielen lieben Dank für das durchlesen und reinfuchsen, ihr seid die Besten!

P.S.: Wenn ihr Fragen zu meinen Rechenvorgängen habt (weil unsauber notiert), dann gerne nachfragen. Ich bin euch sehr verbunden.

Kann jemand mir helfen in dieser Aufgabe?

Bin verzweifelt, kann das jemand lösen?

Bisher:

a) 150 Bakterien

b) Nach 4h verdoppelt, nach 8h vervierfacht

Wäre sehr dankbar , falls das jemand lösen kann...:)

ein Rechteck hat den Umfang 30cm, wobei die eine Seite 2 cm länger ist als die andere Seite. Wie lang sind die Seiten?

Hallo, wie löse ich diese Textaufgabe ohne Taschenrechner?
Mit Taschenrechner ist sie sehr einfach aber ohne komme ich nie an die Antwort.

9 medizinische Mitarbeiter benötigen 4 Stunden um 140 Personen zu impfen. Wie lange benötigen 16 medizinische Mitarbeiter, um 350 Personen zu impfen?

Die Antwort Lautet: 5 Stunden, 37 Minuten und 30 Sekunden.

Danke für jede Hilfe :)

LG Flobin

Danke im Voraus!

Also wenn man es jetzt händisch mathematisch aufschreiben würde, was wäre es? Weil ich kenne z.b. sowas wie „-2* Z.2“ etc.

Also, das sind 5.-Klässler-Aufgaben. Ich habe es selbst in einer Minute durchgerechnet und mit dem Taschenrechner nachgerechnet. Nichts ergibt 25, aber es soll dennoch falsch sein.

Ich habe das folgende LGS gegeben:

2a-3b+1c=1

1a-1b+1c=0

1a-1b+1c=0

nun habe ich es mit dem Gauß-Verfahren so aufgelöst:

1a-1b+1c=0

0a-1b-1c=1

0a+0b+0c=0

x3 ist damit ja gleich x3, ist das dann 1?

wenn ja, dann ist x2= -2 und x1=2 oder muss ich das mit variablen machen? Also letzten Endes ist meine frage, was ist meine Lösungsmenge, wie stelle ich die auf??

Hallo miteinander, ich benötige Hilfe beim Lösen, von folgendem Gleichungssystem.
Leider komme ich nicht auf die richtige Lösung (x=-3 und y=-3) egal was ich mache.
Die Aufgabe ist auch mit dem Einsetzungsverfahren zu lösen

2x-11y=27

6x+9=3y

Ich habe zunächst die erste Gleichung mit 3 multipliziert, und die zweite nach 6x umgestellt

6x-33y=81

3y-9 = 6x

Danach habe ich eingesetzt

6 (3y-9) = -33y = 81

18y - 54 - 33y = 81

-15y = 135 mit -15 dividiert

y= -9

Wo ist hier genau mein Fehler?

Es gäbe auch die Möglichkeit die zweite Gleichung mit 2 zu dividieren

2x + 3 = y

nach 2x umstellen

2x = y - 3

Einsetzen

2 (y - 3) - 11y = 27

2y - 6 - 11y = 27 plus 6

-9y = 33 dividieren mit -9

y = 3 1/3

Hallo habe eine Aufgabe bezüglich den kern einer Matrix berechnen gelöst doch bin auf Probleme gestoßen so, dass ich es nicht lösen konnte. Kann mir jemand bitt dringend helfen.

Ich bedanke mich im Voraus.

Bestimmen sie Die Lösungsmenge des linearen Gleichungsystems. Interpretieren Sie das lineare Gleichungsystem und die Lösungsmenge geometrisch.

x+y-z=2

x+z=1

2x+y=5

Ich habe das lineare Gleichungsystem gelöst und keine Lösung raus. Allerdings steht in der Lösung, dass man trotzdem die Schnittgeraden herausfinden kann da die Normalvektoren orthogonal zueinander sind. Doch wie finde ich die 3 Schnittgeraden heraus?

Guten Tag,

leider bereitet mir der Aufgabenteil e) noch Schwierigkeiten. Ich verstehe es leider noch nicht, wie ich die Anzahl der Lösungen eines Gleichungssystems im allgemeinen bestimmen kann.

Ich freue mich über hilfreiche Antworten

Wenn jemand an der Universität (oder FH) das Modul ,,Lineare Algebra" mit einer 2.0 besteht, wie hoch seht ihr die Wahrscheinlichkeit, dass derjenige Analysis ebenfalls besteht?

Ich habe die LGS gelöst und für (1) keine Lösung, also gehört sie zu Fig. 5. Die anderen beiden haben eine lösung, aber wie unterscheide ich die Fig. 4 und Fig.6 an der Lösung des LGS..?

Hallo leute,

ich hab da so ein problem. Ich verstehe nicht warum der winkel alpha im kleinen grünen dreick gleich dem winkel alpha im großen roten dreieck ist kann mir das jemand erklären.
(vielleicht erkennt es ja der eine oder andere es geht um die Interferenz beim doppelspalt aber das ist irrelevant für die winkelbeziehung, wollte nur mal erwähnen wofür ich das brauche)

Guten Tag,

aktuell befasse ich mich mit linearen Optimierungsproblemen in allgemeiner Form.

Nun wurden die künstlichen Variablen eingeführt. Ich verstehe nicht so ganz, was sie für einen Nutzen haben und wann man eine Ecke des Zulassungsbereiches des ursprünglichen Problems mit den Variablen und Schlupfvariablen erreicht.

Genauer geht es um die erste Phase der Zweiphasenmethode. Kann mir diese jemand (allgemein) erklären?

Es ist wahrscheinlich viel Arbeit, weswegen ich auch für hilfreiche Links dankbar bin.

Hey Leute,

Bin grad an Mathe lernen und habe eine Frage. Wenn man minus wurzel und dann eine Zahl hat, ergibt es dann eine Positive Zahl oder eine negative?

Bei mir gehts irgendwie nicht auf...

Ich habe da 0,6666667 raus, Photomath sagt aber das stimmt nicht? Ich habe die Gleichsetzung gemacht.

Ich habs mit dem Gauß-Verfahren probiert, kam aber nicht weiter. Kann mir jemand bitte Schritt für Schritt die Rechnungen erklären?

Ich habe bereits auf ,,Photomath‘‘ probiert diese Aufgabe zu lösen, habe es dennoch nicht ganz verstanden…

Danke im Voraus!

Bei der im Bild gezeigten Aufgabe handelt es sich um eine Folgeaufgabe. Kann mir jemand erklären, wie man bei Aufgabe c) zu den Antworten gekommen ist? Ich versteh nicht was da gerechnet wurde. Danke im Voraus

Habe ich diese Aufgabe richtig gerechnet?

Bin mir nicht sicher was "min" bedeutet ich vermute einfach das minimum von irgendeiner Menge. Es ist ja nicht beschriftet mit einer Einheit wie €, kg, l etc.

Um Gleichungssysteme mit vielen Unbekannten zu lösen?