Wie bestimme ich die Anzahl der Lösungen eines LGS?
Guten Tag,
leider bereitet mir der Aufgabenteil e) noch Schwierigkeiten. Ich verstehe es leider noch nicht, wie ich die Anzahl der Lösungen eines Gleichungssystems im allgemeinen bestimmen kann.

Ich freue mich über hilfreiche Antworten
3 Antworten
Wie bestimme ich die Anzahl der Lösungen eines LGS?
Grundsätzlich gibt es drei Möglichkeiten:
1) Es gibt genau eine eindeutige Lösung: Dies ist der Fall, wenn die Anzahl der Gleichungen im System gleich der Anzahl der Unbekannten ist und wenn alle Gleichungen linear unabhängig sind.
2) Es gibt keine Lösung, wenn die Gleichungen widersprüchlich sind. Dies kann z.B. sein, wenn eine Gleichung einen Widerspruch enthält, z.B. 0 = 1 oder wenn beim Lösen des LGS ein solcher Widerspruch auftritt.
3) Ein LGS hat unendlich viele Lösungen, wenn die Anzahl der Gleichungen kleiner ist als die Anzahl der Unbekannten und die Koeffizientenmatrix des Systems nicht vollen Rang hat. Dies tritt auf, wenn mindestens eine Gleichung im System als Linearkombination anderer Gleichungen ausgedrückt werden kann.
Zur Festsellung, welche der drei obigen Möglichkeiten zutrifft, kenne ich zwei Verfahren:
1) Lösen des LGS mit Gauß. Da kommt am Ende raus: z = z und das bedeutet, für z gibt es keine eindeutige Lösung, also gibt es unendich viele Lösungen.
2) Man bestimmt den Rang der Koeffizientenmatrix, was vom Prinzip aber auch nicht viel anders ist als Gauß, bloß dass man etwas früher abbrechen kann an dieser Stelle:
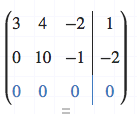
Sobald eine Zeile komplett nur Nullen hat, und nur 2 linear unabhängige Zeilen übrigbleiben (= Rang 2), kann man abbrechen und feststellen, dass es unendlich viele Lösungen gibt.
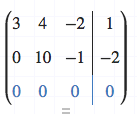
3 4 -2 1 ...............(1)
-6 2 3 -4 ...............(2)
0 10 -1 - 2 ...............(3)
. Nullen erzeugen
(1) mal 2 zu (2) macht (2a)
0 10 -1 -2 ...............(2a)
.
(2a) mal -1 zu (3) macht (3a)
0 0 0 0
.
3 4 -2 1 ...............(1)
0 10 -1 -2 ...............(2a)
0 0 0 0 ...................(3a)
.
Eine solche letzte Zeile (nur Nullen) heißt , es gibt unendlich viele Lösungen
.
Man kann sich bei (3) ein y oder z aussuchen : y = 0 , dann z = +2
und x ( mit (1) )
3x + 0 - 4 = 1
x = 5/3
L = { 5/3 ; 0 ; 2 }
.
Probe mit (1)
3*5/3 + 4*0 - 2*2 ? = ? 1
5 + 0 - 4 = 1 jo
.
oder man wählt das x = 5
3*5 + 4y - 2*(10y + 2) = 1
15 + 4y - 20y - 4 = 1
-16y = -10
y = 10/16
.
10*10/16 - z = -32/16
(100+32)/16 = z
132/16 = z
L = {5 ; 10/16 ; 132/16}
.
Probe
3*80/16 + 4*10/16 - 2*132/16 = 16/16
(240 + 40 - 264)/16 = 16/16
(280-264)/16 = 16/16 jo
.
Ps man kann sich zugleich auch zwei aussuchen x und y , x und z , y und z
aber nicht y und z
Warum ?
Du kannst das LGS Gaußen und dann den Lösungsraum bestimmen. Dieser ist ein affiner Unterraum, in dem alle Lösungen enthalten sind.