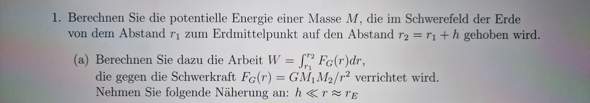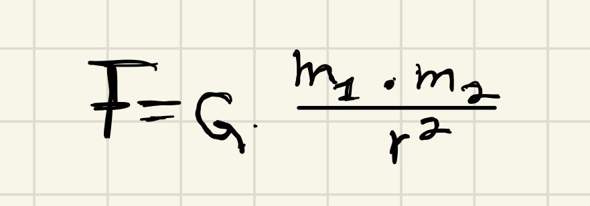Ich habe einmal gehört, wenn die Gravitation nur geringfügig schwächer wäre, würde das Universum auseinanderfliegen und es gäbe weder Planeten noch Sterne, und wenn die Gravitation ein klein wenig stärker wäre, würde das Universum einfach in sich selbst zusammenfallen. Was hält die Gravitation im Gleichgewicht? Ich meine, wenn das Verhältnis zwischen der elektromagnetischen Kraft und den Auswirkungen der starken Wechselwirkung nicht 1 % betragen würde, gäbe es kein Leben. Ich würde gerne die Quelle nennen, aber ich habe leider vergessen, woher ich diese Informationen habe, ich weiß nur noch, was da drin stand.

Wie heißt die Gegenkraft zur Gravitationskraft?

nach Newton3 muss es die ja geben

Nehmen wir an, zwei Schwestern wohnen übereinander. Bei Olga, die oben wohnt, vergeht die Zeit langsamer als bei Uschi, die unten wohnt. Es sind zwar nur winzige Sekundenbruchteile pro Tag, aber nehmen wir an, es wäre etwa 1 Sekunde. Der Tag hat also für Olga nur 23:59:59 h. Dennoch sehen beide jeden Tag gleichzeitig die Sonne genau im Süden. Wie kann man das erklären?

Wenn man eine hohle Erde hat und da drinnen dann eine Masse. Wirkt auf die Masse eine Kraft?

#Physik #Gravitation

Sagen wir es gibt keinen Luftwiderstand usw. Und dann würde man irgendwo unendlich lange runterfallen. Würde man dann theoretisch unendlich schnell werden und somit schneller als Lichtgeschwindigkeit werden? Denn wenn etwas fällt wird es ja immer schneller

Moin,

(Im Internet duzt man sich!)

also, deine Profession und meine Erwartungen passen nicht so richtig zusammen. Ich stelle trotzdem meine Fragen!

Die Theorien zur Entstehung und der Ausbreitung des Universums und die Mathematischen Modelle /Simulationen passen ja nicht richtig zueinander.

Wo denkst du liegt der Fehler bzw. wie denkst du über meine "unprofessionelle" Fehleranalyse ?

1. Müsste man deiner Meinung nach, reale Experimente im Weltraum zum Thema Ursache und Verhalten der Schwerkraft durchführen um dort vielleicht Fehler zu finden.
2. Müsste man vielleicht die Lichtgeschwindigkeit und die größtmögliche 'Geschwindigkeit im Universum' als 2 Werte betrachten, das Licht eine 'extrem kleine' Masse hat, aber die größtmögliche Geschwindigkeit im Universum nur eine theoretische Zahl 'ohne Masse' sein sollte. (Jede Masse könnte man theoretisch teilen..)
3. Die Ausdehnung des Universum schneller als das Licht eigentlich unter Beachtung der Relativitätstheorie ein ziemlicher Unsinn ist. Vor allen, das man das Universum nur von der erde aus betrachtet ... und man die Grundgeschwindigkeit unserer Galaxie gegenüber dem Leeren Raum gar nicht absolut ermitteln kann. (außer mithilfe eines Vergleichs alle Geschwindigkeiten und mithilfe des Höchstpunktes Lichtgeschwindigkeit ...) Bewegen sich Galaxien im Universum in allen Richtungen schneller als das Licht von unserer Milchstraße weg ? ...

Grüße

Kann ich einen Pool für 2 Leute auf den Balkon stellen? Oder kann da was passieren? Wohne im ersten Stock

Ist Gravitation wie eine Kraft dessen Energie die Masse ist?

Dann würde Gravitation doch nie enden oder unter Umständen sich nur verteilen falls die Grundmasse zerstört und verteilt wird in kleinere Massen mit jeweils weniger Gravitation

Würde z.B. eine Masse in 4 gleiche Massen geteilt werden, würden die 4 Gravitationskräfte der kleineren Massen addiert nun wieder die Gravitation der großen Masse ergeben? Oder steigt die Gravitation zu seiner Masse nicht proportional?

Wenn man mit einem Fahrrad einen leicht nach unten gehenden Hügel fährt, treibr man das Fahrrad garnicht an aber fährt immer und immer schneller durch Gravitation

Ist das dann nicht eine sozusagen (unendliche) Energiequelle?

Könnte man nicht aus Gravitation irgendwie Energie ziehen?

Lässt Gravitation mit er Zeit nach und ist somit begrenzt??

Eine etwas ältere Theorie besagt, dass sich die Erde allmählich ausdehnt.

Dinosaurier konnten so groß sein, weil die Erde kleiner und die Schwerkraft daher geringer war. Heute würden die ganz großen Dinosaurier unter ihrem Gewicht zusammenbrechen.

https://www.youtube.com/watch?v=AlscDg5zXXk

11:30 bis 19:00

Um die Gravitation zu erhalten soll ein Stahlseil zwischen Erde und Sonne gespannt werden. Es soll ein Stahlseil mit einer Zugfestigkeit von 1000 MP (1kN/mm²) verwendet werden, das bis zur Grenzlast belastet werden soll.

1.   Bestimmen Sie den Querschnitt des Stahlseils

2.   Vergleichen Sie den Querschnitt des Seil mit dem Erdquerschnitt.

Erdmasse: 5,9722 · 10²⁴ kg 

Erdumlaufdauer 31,6 . 10⁶ s

Erdradius 6370 km

Sonnemasse: 1,989·10³⁰ kg   

Gravitationskonstante: 6,6743^.10^-11 m³/(kgs²)

Wäre nett, wenn mir jemand mithilfe eines Rechenwegs weiterhelfen könnte.

Vielen Dank schonmal im Voraus...

Hallo gutefrage-Community,

ich wollte fragen, wie hoch die Gravitation auf Höhe des ISS-Orbits noch ist. Die ISS befindet sich auf einer durchschnittlichen Höhe von ca. 400 km

Die allgemeine Relativitätstheorie besagt ja zum einen, dass die Gravitation eine Scheinkraft ist. Etwas, was wie eine Kraft wirkt, aber eigentlich inexistent ist.
Eine Masse krümmt die Raumzeit. Nun gibt es eine 4-Dimensionale Krümmung. Befindet man sich in dieser Krümmung, dann wird man in Richtung des Mittelpunktes der Masse beschleunigt. Das wirkt wie eine Anziehungskraft, die jedoch nicht da ist.
Meine Frage ist, warum man denn in einer Raumzeitkrümmung zum Mittelpunkt beschleunigt wird? Was wirkt denn da?

Ich werde einfach nicht fündig und zerbreche mir den Kopf.

Ab welcher Entfernung zur Sonne ist man weit genug von der Sonne entfernt um nicht mehr von der Anziehungskraft/ Gravitation der Sonne/ des Sonnensystems beeinflusst zu sein? Km, AE angaben oder sonstige ist egal.

Ich versuche mir folgendes vorzustellen:

Die Erde dreht sich um die sonne und das Sonnensystem um das Zentrumder Galaxie. Wie weit muss ich theoretisch Reisen, damit sich sich das Sonnensystem weiter dreht und mich zurück lässt?

Wie nennt sich die "Barriere"?

Vielen Dank schon mal!

(Falls es jemand weiß interessiert mich auch direkt wie schnell nach aktuellem stand, das schnellste unbemannte Raumschiff fliegen kann)

Danke 😀

Warum war er so überrascht wegen dem Apfel. War es nicht sowieso klar, dass es fallen würde?

Hey, ne, es is ja so, dass Corum direkt im Erdmittelpunkt liegt. Müsste dann die Fallbeschleunigung nicht ziemlich hoch sein? Wie groß?

Hallo zusammen,

in der letzten Zeit habe ich vermehrt Videos gesehen in denen beschrieben wurde, dass würde man mit einem Raumschiff am Jupiter vorbeifliegen, man aufgrund seiner enormen Gravitation nach vorne geschleudert wird. Wie kann ich mir das denn vorstellen, ich dachte immer Gravitation zieht Dinge an.

Danke schonmal für die Antworten

Wie kann man einen Planeten wiegen?

Ich bin euch wirklich dankbar, wenn irgendjemand mir die Gleichungen auf der letzten Seite erklären kann, die ich dem dem originalen Werk von Cavendish entnommen habe ( die Bestimmung der Dichte der Erde) und wie man dazu kommt. (Hinweis: es hat mit Verhältnissen, dem Drehmoment und der Frequenz etwas zu tun)

Diese mathematische Formulierung treibt mich seit langem um.😀

Der Zusammenhang mit seinem Versuch geht aus dem Kontext hervor!!!

Vielen Dank im Voraus!!!

Hallo,

ich soll einen eher umgfangreichen Vortrag zum Thema "Gravitationsgesetz" im Physik LK ausarbeiten.

Thematisch habe ich keine Vorgaben, habe allerdings Schwierigkeiten mir selber einen roten Faden zu spannen, bzw. komme nicht auf den angesetzten Umfang.

Bis jetzt habe ich etwas zu dem universellen und dem Newtonschen Gravitationsgesetz geschrieben.

Hat jemand eventuell noch Ideen, worüber ich noch schreiben kann bzw. wie genau er das Referat gliedern würde?

Falls sich jemand gut mit dem Thema auskennt, würde ich mich sehr über Hilfe freuen!

Liebe Grüße

Welches Teilchen ,welches Feld sorgt dafür,dass die uns bekannte Materie mit ihrer Masse sich gegenseitig anzieht

Ist die Gravitation nichr von beiden Massen abhängig? Die Formel geht ja F = G× (m1 × m2 / r²). Dann müsste etwas was eine Tonne schwer ist stärker angezogen werden, als etwas, daas ein Kilogramm schwer ist.

Wenn man sich vorstellt, man hätte die Möglichkeit, am Nordpol ein Loch zu graben durch den Erdkern hindurch, und am Südpol wieder raus zu kommen.

Und das ein Mensch unbeeinflusst von Druck und Geschwindigkeit, einen Sprung in dieses Loch an der nördlichen Seite wagen könnte. Was würde passieren?

Also die Sxhwerkraft sagt ja, das alles nach unten fällt. Aber am Südpol gilt ja die selbe Schwerkraft, also was wirkt auf dem Körper? Wird der am Süden ins Weltall gepustet, wegen der Beschleunigung? Dreht sich die Erdanziehung doch irgendwie und er bleibt am Erdkern stecken? Fällt er ewig hin und her?

Was würde rein physikalisch passieren (wenn man außen vor lässt das die Person stirbt und am Erdkern verbrennt)

Was ist der Hauptgrund Flacherdler glauben die Erde wäre Flach? Gibt es dan icht massive Probleme? Wie z.b. Gravitation, und das Schiffe am Horizont verschwinden, und vieles vieles mehr.

Haben Flacherdler meist religiöse Gründe, warum sie einen Globus ablehnen? Und was würde Flacherdler von einem Globus überzeugen?

Große Massen krümmen Raumzeit, womit Gravitation doch lediglich eine Scheinkraft darstellt, ähnlich der "Zentrifugalkraft" welches ja ebenfalls keine Kraft im physikalischen Sinne darstellt, sondern lediglich die Auswirkung auf ein Objekt, welches sich einer Beschleunigung widersetzt. Allerdings wird Gravitation munter als beides dargestellt, sowohl als die Konsequenz von Raumzeitkrümmung als auch als physikalische Grundkraft. Kann denn beides zutreffen, und so nicht, müsste dann nicht eine der beiden Darstellungen verworfen werden müssen?

Die schwache, starke und elektromagnetische Wechselwirkung können alle entgegengesetzt wirken, jedoch die Gravitation aber nicht. Gibt es hierfür schon eine Erklärung warum dies so ist?

Angenommen er würde von genug Kometen getroffen werden dass er einen kritischen Punkt überschreitet und die Kernfusion beginnt.

Gedankenexperiment auf zwei Ebenen:

1. Alle Umlaufbahnen bleiben dieselben, alle Planeten und der Jupiterstern kreisen weiterhin um die Sonne

2. Jupiters Masse nimmt so stark zu dass ein Doppelsternsystem entstünde.

Natürlich rein theoretisch gesehen.

Guten Tag allerseits,

bald halte ich eine Präsentation über das Newton’sche Gravitationsgesetz und es gibt noch ein paar Unklarheiten.

Alle Körper fallen prinzipiell -wenn man den Luftwiderstand nicht berücksichtigt- ja gleich schnell auf die Erde, mit einer Fallbeschleunigung von 9,81 m/ s^2.

Was bringt mir dann die Formel zur Berechnung der Gravitationskraft? Wenn ich beispielsweise die Gravitationskraft zwischen der Erde und einem Stein berechne, kommt F≈ 0,26N als Ergebnis raus.

heißt das, dass eine Kraft von 0,26N benötigt wird, damit der Stein von der Erde angezogen wird?

Und noch eine Frage:

sollte ich in meiner Präsentation auch die Fallbeschleunigung erwähnen?

Danke schonmal und liebe Grüße :)

Hey allerseits, ich halte bald eine Präsentation über das Newton‘sche Gravitationsgesetz.

Als Beispiel möchte ich die Gravitationskraft von einem Stein zur Erde berechnen.

Masse der Erde: 5,97*10^24kg

Masse des Steines: 30g

Formel: F= G* m* M / r^2

Nehmen wir an, der Stein fällt von einer Höhe von einem Meter auf die Erde herunter.

Daher beträgt ja nun der Radius zwischen den beiden Massenmittelpunkten 6372km.

Kann ich nun Masse, Radius etc. einfach in die Formel einsetzen, oder muss ich noch bestimmte Einheiten umrechnen, z.B. den Radius von km in m.

Vielen Dank schonmal für eure Antworten.

LG :)

Hallo, ich würde gerne wissen warum das Gravitationsgesetz ein Spezialfall des 3. Newtonschen Gesetzes(Wechselwirkungsgesetz) ist? Ich habe viel recherchiert aber nirgends steht etwas dazu. Ich weiß nur dass bei beiden Gesetzen beide Körper eine Kraft auf den anderen Körper ausüben. Aber gibt es eine richtige Erklärung dafür?

danke im Voraus

Es geht um den Mond und die Erde sowie deren Kräfte. Es ist klar der Mond dreht sich um die Erde, deshalb wirkt eine Zentripetalkraft vom Mond zur Erde und eine Gravitationskraft entgegengesetzt.

Stehe ich aber auf dem Mond als neutraler betrachter dreht sich die Erde relativ zu mir. Wirkt aus dieser Sicht eine Zentripetalkraft vom Mond zur Erde und die Gravitationskraft entgegengesetzt.

oder

kann die Zentritedalkraft nur von Erde zu Mond wirken, unabhängig vom Betrachter.

Das Problem ist man kann vom Mond aus ja nicht erkennen, das man sich um die Erde dreht.

Die Frage rührt ursprünglich aus Folgendem.

Im Physikuntericht sollten wir die Geschwindigkeit des Mondes anhand des Radius und der Masse berechnen. Wir haben dann die Fg und Fzentripetal gleichgesetzt nach v umgeformt und sind auf

V = (Gamma * M(Erde) / r^2) ^0,5

gekommen.

So weit so gut Ergebnis kam auch soweit hin zumindest hat der Physiklehrer nichts anderes gesagt.

Ich habe mich dann gemeldet und gesagt:"Wenn man statt M(Erde) einfach M(Mond) einsetzt, würde man die Geschwindikeit der Erde um den Mond berechnen.

Diese sollte die gleiche sein weil in gleicher Zeit eine Umrundung mit gleichem Abstand stattfindet also gleiche Geschwindikeit.

Guckt man sich die Gleichung an stellt man fest, es kommt durch die veränderte Masse ein anderes Ergebnis raus. Das dürfte nach meinem Verständnis nicht sein. Bitte beheben sie meinen Denkfehler."

Meone Frage an euch, wo liegt das Problem. Darf man Fzentripetal nicht gleichsetzen wegen der oberen Frage oder etwas anderes. Mein Physiklehrer konnte mir nicht weiterhelfen, er hat es selbst nicht durchblickt und versprach mir eine Antwort bis Ende der Stunde. Die Stunde ist um, er weiß keine Antwort und nun frage ich euch. Ich und mein Sitznachbar haben schon über die Relativitätstheorie nachgedacht, dafür sind die Massenunterschiede allerdings viel zu klein.

Könnte mir jemand mit dieser Aufgabe helfen, weil ich sie nicht ganz verstehe?

"Ein junger Mann bestimmt die Masse seiner Freundin durch folgenden Versuch: Beide stellen sich einander zugewandt auf ihre baugleichen Skateboards und stoßen sich dann mit den Händen voneinander ab. Nach dem Abstoßen besitzt sie eine Geschwindigkeit von 3,1 m/s, seine beträgt -2,5 m/s. Er hat eine Masse von 78,8 kg. Die Skateboards haben jeweils eine Masse von 5,0 kg. Wie schwer ist sie?"

Danke im Voraus!

Der ansatz: Epot (vErde) + Ekin (v0)= Epot (rE+h) + Ekin (vUmlauf)

ich verstehe nicht wieso drei Geschwindigkeiten im ansatz sind. Was ist vE und vUmlauf? Die gesuchte Größe ist doch v0 die startgeschwindigkeit oder nicht? Kann mir einer weiterhelfen?

Hallo allerseits,

Ich befasse mich gerade mit der allgemeinen Relativitätstheorie, nachdem mich die spezielle Relativitätstheorie schon so erstaunt hat.

Einer der wohl wichtigsten Erkenntnisse dieser allgemeineren Theorie Einsteins für Systeme, die sich nun eben z.B. beschleunigt bewegen und keine perfekten Inertialsystem darstellen, ist ja die „neue“ Beschreibung der Gravitation. Diese ist ja mit Newtons Axiomen nicht vereinbar und erscheint aus heutiger Sicht dieses Phänomen besser und „realistischer“ zu beschreiben.

Nun zu meiner Frage. Laut Newton kann sich eine Gravitation mehr oder weniger unendlich schnell ausbreiten und die Gravitationskraft zweier Körper geht bis ins Unendliche (auch wenn diese dort extrem klein wird). Laut Einstein kann sich die Gravitation bzw. die Krümmung der Raumzeit ja maximal aber nur mit der Lichtgeschwindigkeit ausbreiten. Gilt diesbezüglich dann nach der allgemeinen Relativitätstheorie aber auch eine „unendliche“ Gravitation oder anders formuliert reicht die Krümmung der Raumzeit, die durch einen massereichen Körper (z.B. ein Planet), ebenfalls bis ins Unendliche und schwächt halt immer mehr ab? Wenn dies so wäre und man sich das Ganze graphisch im einfachsten Sinne veranschaulicht mit einem dreidimensionalen Raumzeitmodell, statt den eigentlichen 4 Dimensionen, würde dies dann bedeuten, dass es in unserem Universum eigentlich keine Stelle gibt, an der es keine Krümmung der Raumzeit gibt? Auch wenn diese Krümmung wie gesagt extrem klein wäre und man mal zunächst von Spezialfällen, wie Schwarzen Löchern absieht…

Ich hoffe meine Fragen sind verständlich. Falls ich etwas falsch verstanden habe oder ihr eine Antwort darauf habt, lasst es mich bitte wissen. Vielen Dank schon im Voraus!

LG

Waagen auf der Erde messen die Kraft, die durch einen Körper im Gravitationsfeld der Erde wirkt geteilt durch 9,81m/s^2.

Mir ist der unterschied zwischen Trägheit und Gewicht schon bewusst. Auf der Erde sind beide numerisch gleich.

Aber warum sagt man nicht einfach:

Ich will Rindfleisch im Wert von fünf Newton kaufen.

Anstatt das man ein halbes Kilogramm haben will?

Schon mal im Voraus: Ich hab nicht viel Ahnung stelle mir trotzdem diese Frage:

Wenn man in einem "Raumschiff" ist...kann man ohne diesen Anzug atmen schwebt aber trotzdem rum. Draußen also wirklich im Weltall braucht man diesen Anzug aber schwebt auch...meine Frage also: Warum kann man im Raumschiff ohne diesen Anzug atmen aber draußen nicht obwohl es ja das gleiche ist weil man draußen und drinnen "schweben" kann?

Die früheren Menschen konnten bestimmten, dass der Radius der Erde r = 6400km beträgt. Sie haben dann die Gravitationskonstante gemessen und haben daraus geschätzt, dass die Erde 6,4*10^24 kg wiegt.

Wie lautete ihre Gravitationskonstante , die sie vermessen haben ?

Ich weiß nicht wie man das lösen soll :(

Die Entfernung vom Mond zum Mittelpunkt der Erde variiert zwischen 363,300 km und 405,500 km, die Umlaufperiode beträgt 27,322 Tage. Ein Satellit umrundet die Erde mit einer Entfernung zur Erdoberfläche von 225km - 710 km. Der durchschnittliche Erddurchmesser beträgt 12,756 km. Was ist die erwartete Periodendauer T für den Satelliten?

Die Antwort sollte T≈1,6h sein, doch wie berechne ich es?

Ich weiss das 3. Kepler Gesetz heißt T ist proportional zu a^(3/2). a ist soweit ich weiss der größte Durchmesser der elipsen (oder Radien).

Also müsste doch eigentlich folgendes gelten:

T_2*a_2^(3/2) = T_1*a_1^(3/2)

oder?

Auf jeden Fall kommt wenn ich es nach T_1 umforme ein total falsches Ergebnis raus :(

Also wenn ich mich einen Meter über der Erde an einer Stange festklemme oder mehrere tausend Meter auf einem Berg einen Felsen hochklettere, ist an beiden Orten die Erdanziehung gleich stark?

Gibt es Unterschiede wenn ich mich auf einer Plattform befinde wie z.B. in einer Bahn?

Hallo Leute,

ich schreibe morgen einen Test über Gravitation. Dazu müssen wir auch über eine Einheitenbetrachtung der Kosmischen Geschwindigkeiten wissen… Kann mir bei dieser vielleicht jemand behilflich sein?

Liebe Grüße

Ida :)

Das habe ich bereits…

Wenn man im Internet schaut wird oft folgendes Experiment beschrieben:

Spannt man ein Laken und legt in dieses Laken einen schweren Gegenstand entsteht eine Delle. Im All wird der Raum gekrümmt. Legt man anschließend eine Murmel auf das Laken rollt diese runter, zum schwereren Gegenstand. Mit diesem Beispiel wird die Gravitation vereinfacht erklärt.

Meine Frage:

Wie kann z.B. ein Planet (die Murmel) den Raum (das Laken) „hinunter rollen“, wenn noch keine Gravitation existiert?

Würde diese Murmel das Laken auch in der puren Schwerelosigkeit herunter rollen?

Wenn man einen langen Eisenstab nimmt und diesen vertikal aufstellt, dann in der Mitte des Stabes eine Wärmequelle platziert und beobachtet an welchem Ende als erstes eine Temperaturänderung auftritt. Oder beide Enden gleichzeitig wärmer werden? Vielleicht ist die Frage dumm weil ja Energie übertragen wird und die nicht von der Gravitation beeinflusst wird.

Falls der vermutete Effekt durch die relativ geringe Beschleunigung der Gravitation auf der Erde nicht messbar ist könnte man den selben Versuch mit einem sich schnell drehenden und einem nicht drehenden Stab machen um die Zentripetalbeschleunigung zu nutzen. Das Ganze natürlich im Vakuum. Dann wird gemessen ob die Enden des sich drehenden Stabs schneller warm wurden oder eben nicht.

Hey Leute

Mein Know-how über Planeten ist abhängig von laienhafter Recherche. Ich suche auch nicht nach total tiefer Wissenschaft, aber ein bisschen mehr Verständnis.

Mir bekannt ist:

-Gravitation ist abhängig von der Maße eines Körpers (mehr Maße = mehr Gravitation)

-Magnetfeldstärke hat was mit der Rotation des flüssigen äußeren Erdkerns zum innerem Erdkern zu tun, wie ein Dynamo.

Meine Fragen:

1) Gibt es eine konkrete Abhängigkeit zwischen Gravitation und Magnetfeld? Mehr Masse auch mehr/größeres/stärkeres Magnetfeld?

2) Welche Faktoren spielen bei der Gravitation und des Magnetfeldes eine Rolle?

3) Welche Abhängigkeit gibt es zur Planetenrotation dabei?

4) Würde ich mehr Materialien auf einen Planeten schaffen, steigt die Masse und mehr Gravitation wird erzeugt? Oder wie würde das Gedankenspiel dabei aussehen, um Gravitation auf einem Planeten zu steigern?

Und auch nicht was der Ursprung ist.

Und auch nicht, was das Wesen der Gravitation ist?

Auch nicht die Ursache?

Das behauptet der Jochen Kirchhoff beinhart und ohne Skrupel gleich am Anfang des Videos!

Zeitstempel:

https://youtu.be/lBu0Eo3zRl0?t=41

ab Min. 0:41

Wenn das stimmt, dann heißt das ja, dass alles was da jemand zu den Fragen meinte, auch falsch ist.

Das ist ja skandalös!

Hi, die Gravitation ist ja so stark das sie uns sogar Kopfüber hält. Sie ist so stark sie hält die Meere zusammen und die Erde. Wie gesagt. Sogar KOPF ÜBER.

Wieso können wir uns dann überhaupt bewegen? Wieso können wir unsere Füße vom Boden überhaupt abgeben.

Wir sind ja nicht stärker als die gravitation die Berge und Meere, Boote Kopfüber hält.

Hey Community,

80 kg Masse auf der Erde hat ein Gewicht von 784N.

Im Weltall fernab von größeren Gravitationsquellen hat sie sagen wir mal nur noch 200N Gewicht.

Hat die träge Masse nun auch nur noch 200 N ?

Vielen Dank im Voraus.

Hey Community,

Wenn die Erde Gravitation ausübt , so erfährt sie die gleiche Kraft wie z.B. ein Apfel.

Nun ist es dass der Apfel Richtung Erdmittelpunkt fällt , aber die Erde ruht weiterhin , sie beschleunigt also nicht. Liegt es daran dass die Masse der Erde wesentlich höher ist als die des Apfels und die Erde deshalb mehr Kraft benötigt um in Bewegung zu geraten?

oder Beschleunigt sie und wir merken davon nichts ?

Vielen Dank im Voraus

Hallo :) Ich weiss die Frage ist etwas „Anders“. Ich bin grade Auf Wolke 11 und schaue grade Intestellar. Die Menschen sind auf einem Planeten wo 1 Stunde auf dem Planeten, 7 Jahre auf der Erde entsprechen. Wieso ist das so ? Ich denke seit 2 Stunden drüber nach und Zerbrech mir den Kopf darüber 😂😂 Vielen Dank leute!

Wer könnte mir mit der Aufgabenstellung helfen? Danke im Voraus.

Berechnen sie die im Gravitationsfeld der Erde zu verrichtende Arbeit um einen Satelliten mit der Masse m=500 kg von der Erdoberfläche in einen Umlaufbahn in Höhe von 36.000 km zu befördern

Wie hoch ist die Gravitationsfeldstärke 50 km über der Erdoberfläche?

Wie kann die Gravitationskraft die einzige Kraft sein die auf den Freien Fall wirkt, wenn der Freie Fall nur im Vakuum und Weltall möglich ist wo es eben keine Gravitationskraft gibt? Danke im Voraus.

Ich lese, daß aus Sicht der Erde ortsfeste Satelliten sich immer in 35.800 km Höhe befinden, weil dann ihre Umlaufgeschwindigkeit mit der Rotationsgeschwindigkeit der Erde übereinstimmt.

Warum gerade da? Kann das jemand physikalisch erklären?

Als Laie hätte ich gesagt, da es keinen Absolutpunkt im Weltraum gibt, könnte ein Satellit durch, laienhaft ausgedrückt "beschleunigen" und "bremsen" sich in jede beliebige Position begeben, aber so einfach ist das anscheinend nicht.

Ist es richtig, dass eine Person, die am Aequator z.B. 60 kg wiegt, am Nord oder Suedpol etwas mehr wiegt, z.B. 63 KG und das sie an den Polen wenige Zentimeter kleiner als am Aequator ist wegen der unterschiedlichen Gravitationwirkung und der Koerper mehr zusammengedrueckt wird?

Hallo liebe Forumfreunde,

ich komme auch mit folgendender Aufgabe nicht wirklich zurecht, dea ich befürchte die AUfgabe nicht richtig verstanden zu haben.

Die Aufgabe lautet: Im Innern der Erde zählt für die Gravitationskraft nur die Masse jener Kugel, deren Radius gleich der Entfernung des betrachten Punktes vom Erdmittelpunkt ist. Homogene Massenverteilung vorausgesetzt, berechne man

a) die Gravitaionsfeldstärke in 1000km Tiefe

b) die Abhängigkeit der Gravitationsfeldstärke im Innern der Erde vom Abstand vom Erdmittelpunkt.

Ich danke im voraus

Mit Freundlichen Grüßen

Also was ich mich da halt Frage: Wie weiss man, dass die Gravitation keine normale Kraft ist wie z.B Em? Gravitationswellen könnte es doch auch so geben, oder nicht? Es gibt ja auch Lichtwellen die erzeugt werden.

Ist Gravitation nicht eine Scheinkraft? Eine Masse krümmt die Raumzeit, wodurch alles in die Krümmung, äh ja ,,reinfällt"?, dies wirkt dann wie eine anziehende Kraft und ist deshalb eine Scheinkraft. Ist das so richtig? Verbessert mich bitte.

Sagen wir er hat einen Durchmesser von 160km und somit etwa 2,1 Millionen Km^3. Er besteht hauptsächlich aus Stahl und wiegt somit 18 Millionen kg. Da natürlich nicht alles zugebaut ist ca. 13 Million kg. Was für einen Abstand würde dieser zur Erde benötigen, um eine sichere Umlaufbahn zu haben?

Mich würde mal interessieren wann es antigravitations Fahrzeuge geben wird schwebende Autos oder Raketen usw

Gegen die Gravitation aus der Masse der Erde wirkt die Fliehkraft aus der Rotation der Erde um ihre eigene Achse. Wenn ich mich wiege, erscheine ich durch die Fliehkraft also leichter als ohne. Wenn die Erde diese Rotation nicht mehr aufweisen würde, wie viel Prozent mehr würde dann eine Waage anzeigen?

Wasser fließt immer dort, wo es am leichtesten ist zu fließen. Ein Blitz bildet sich auch genau so, wie es für ihn am leichtesten ist einzuschlagen.

Würde Wasser nach oben fließen, so würde es die Gesetze der Physik umgehen (unter normalen Bedingungen).

Müsste das nicht heißen, dass auch der Mensch, welcher Teil der Natur ist und auch den physikalischen Gesetzen unterliegt, entsprechend seiner Denkweise immer den Weg des geringsten Widerstandes geht?

Dass, wenn ich die Wahl habe, mich auf den Boden zu legen oder einen Berg zu erklimmen, selbst das erklimmen des Berges der Weg des geringeren Widerstandes ist, wenn ich das intensive Verlangen danach habe, es dann sogar leichter für mich ist, den Berg zu erklimmen, als mich hinzulegen? Natürlich nur solange mein System mir sagt: "Ne, jetzt will ich doch liegen!", und dann das hinlegen der leichtere Weg ist.

Habe von einer Theorie gelesen, dabei ging es darum was auf langzeit mit dem Universum & der beschleunigung nach dem Urknall passiert. Es gab 3 Theorien:

1.Das Universum expandiert immer und immer weiter.

2.Es expandiert und kommt irgendwann zum Stillstand

3. Es expandiert, kommt zum Stillstand, die Gravitation setzt ein und zieht alles wieder in sich zusammen.

Falls Theorie 3 realistisch ist würde dass doch bedeuten, das sich die ganze Masse im Universum wieder an einem Punkt sammelt.

Mit dem Resultat eines extrem Massereichen, extrem winzigen und extrem Instabilen Punkt oder Schwarzem Loch etc.

Was haltet ihr davon ?

Soweit ich weiß spricht ja nichts dafür das die expansion aufhört sondern eher das sie zunimmt.

Wie viel Fläche würde 1 Liter Wasser ungefähr einnehmen wenn man es auf einen geraden Untergrund z. B. eine Glasfläche Schütten würde?

Optional: Wie hoch wäre diese Schicht Wasser unter Normalbedingungen?

Voraussetzungen: Es handelt sich um eine unbegrenzt große Fläche und das Wasser würde nicht verdampfen.

Ich schreibe eine Klausur über das Thema und ich will wissen, wie man die Aufgabe löst.

a) mit der Näherung, dass die Gravitationsfeldstärke konstant ist (wie auf der Erdoberfläche);

b) im radialen Gravitationsfeld der Erde

Hallo ihr lieben das ist meine heutige Physik Distanzunterricht Aufgabe aber leider komme ich nicht weit. (Es ist momentan alles so schwer...)

für a habe ich schonmal folgendes aber ich weiß nicht ob es richtig ist:/

Epot = m*g*h= 1500000g*9,81m/s2*25000000m =?

b verstehe ich leider gar nicht 😩

kann mir bitte jemand helfen?

lieben lieben dank

Erkläre warum dein Federmäppchen auf dem Schreibtisch keine Zusatzgeschwindigkeit erhält, obwohl doch die Gravitationskraft auf das Federmäppchen wirkt.

Die Gravitationskraft ist die eine Kraft. Der Schreibtisch liefert mit dem Boden eine Gegenkraft, die auch auf das Federmäppchen wirkt.

So würde ich das erklären 🤔

Ich muss eine 2 Zeitige Hausarbeit in Physik schreiben. Das Thema darf ich mir aussuchen, solange es mit Weltraum und Gravitation zu tun hat. Es müssen jedoch auch physikalische Berechnungen dabei sein. Wüsste jemand vielleicht welches Thema sich dafür gut eignet? Ich besuche die 10. Klasse eines G8 Gymnasiums. So sollte dann auch der Schwierigkeitsgrad sein. Ich freue mich auf Antworten!

Die Erde durchläuft ihre Bahn in rund 365 Tagen, der Jupiter die seine in 11,86 Jahren. Legen Sie für die folgenden Rechnungen Kreisbahnen zugrunde. Vergleichen Sie durch Berechnung die Strecken, welche die Erde bzw. der Jupiter in einem Tag zurücklegen.

Mein Problem und Ansatz lautet:

Ich weiß nicht jetzt wie ich genau vorgehen soll. Meine erste überlegung ist es 2πr für den Umfang der kreisbahnen zu nehmen. Weiter komm ich nicht.

Danke im Voraus für die Hilfe. : )

Wie komme ich mit den Werten gamma (Gravitationskonstante) =6,67x10^-11m^3/kg*s^2; a (Fallbeschleunigung) =9,81 m/s^2; Erdradius 6370km auf die Erdmasse?

Form des Körpers, Farbe des Körpers oder Masse des Körpers?

hallo, ich bin mir bei einer Aufgabe nicht ganz sicher wie diese Richtung zu lösen ist und wollte fragen ob mir jemand dabei weiterhelfen könnte, die Aufgabe lautet:

Geben sie an, in welcher Höhe über dem Erdboden ein Kilogrammstück die Gewichtskraft 1/4*9,81 N erfährt.

vielen Dank im voraus

Ich bin in der achten Klasse und das ist eine Aufgabe für Physik.

Hallo, ich denke viele hatten schon als kleines Kind den Gedanken, kurz vor einem Flugzeigabsturz einfach rauszuspringen und somit zu überleben. Ich weiß, dass das nicht geht, da du die selbe Geschwindigkeit hast, wie das Flugzeug. Somit müsste man genau die selbe Kraft beim Hochspringen aufbringen, mit der man auf den Boden zurast.

Soweit alles richtig?

Nun zu meiner Frage: Du befindest dich doch in dem Körper, warum hast du dann die selbe Geschwindigkeit z.b. 300km/h wie das Flugzeug?

Die Gravitation nimmt bekanntlich mit dem Quadrat zum Abstand einer Masse ab. Sie wird also immer weniger, aber nie null. Also selbst wenn wir einen unendlich großen Raum hätten, würde die Gravitation einer Masse nie null werden, oder?

Guten Tag,

in meinen Physik Hausaufgaben soll ich herausfinden warum auf den Himmelskörpern(siehe bild(kleine gewichte))eine unterschiedliche Gravitationskraft wirkt.Ich denke es könnte an der Anziehungskraft liegen,weiß allerdings nicht wie ich die Antwort formulieren könnte.

Die Trägheitskraft würde ja eigentlich dafür sorgen, dass sich ein Planet gerade in eine Richtung bewegt, die Gravitationskraft sorgt dafür, dass diese Trägheitskraft abgebremst wird, nun zu meiner Frage: Die Trägheitskraft ist ja eine Kraft, die wenn eine andere Kraft auf sie einwirkt, gemindert wird. Schließlich müssen die ISS und sämtliche Satelliten immer wieder von der Erde weg beschleunigt werden, um nicht irgendwann in die Erde zu krachen. Was also, welche Kraft sorgt dafür, dass die Umlaufbahnen von Planeten nicht dauernd verkürzt werden und sie nicht in die Sterne fliegen? Oder ist es so, dass sie sich langsam den Sternen nähern?

Man nimmt an, dass die Sonne Merkur und Venus verschlucken wird, wenn sie zum Roten Riesen wird.

Es wäre aber möglich, dass sich diese Planeten dann von der Sonne entfernen.

Vergleichen würde ich es mit einem Kettenkarussell. Die Ketten wären dann praktisch die Gravitation der Sonne.

Also wäre es so, dass die Entfernung der Planeten zur Sonne in etwa konstant bleibt. Die Sonne gewinnt ja nicht an Masse und Gravitation hinzu, sondern sie dehnt sich aus und verliert Masse.

Es wäre ähnlich vergleichbar, wie wenn sich ein dichter kleiner Würfelzucker zu einem großen Ball Zuckerwatte ausdehnen würde.

Hi, wie ich hier einem Factsheet der NASA (https://nssdc.gsfc.nasa.gov/planetary/factsheet/uranusfact.html) entnehme ist Uranus deutlich schwerer als die Erde, um genau zu sein fast 15 mal so schwer.

Wie kann es also sein, dass die Anziehungskraft geringer ist?

Ich habe eine Kraft Fg, die an einem Ort r-Pfeil auf eine Testmasse m wirkt. Sie ist gegeben durch - (GmM/r^3) * r-Pfeil, wobei r^3 der Betrag des Ortsvektors ist. G ist die Gravitationskonstante und M die Masse des Objektes, das eine Kraft Fg am Ort r-Pfeil auf klein m ausübt.
Wie kann ich überprüfen oder zeigen, dass es sich hierbei um ein konservatives Kraftfeld handelt, d.h dass die Arbeit von a nach b gleich die negative Arbeit von b nach a ist? Kann ich von der Kraft Fg irgendwie auf die Geschwindigkeit oder so kommen?

Ist 1kg Federn und 1kg Blei auf dem Mond gleich schwer?

Wenn man von Schwere spricht, geht es ja um eine Kraft. Wäre die auf dem Mond gleich groß. Was wäre schwerer?

Vielleicht kann mir jemand dieses physikalische Phänomen erklären

Sind manche Objekte/Stoffe an anderen Orten der Erde schwerer (außer z. B auf dem Nordpol) ?

da die Erde ja als abgeflacht an den Polen gilt und somit die Leute näher am Gravitationszentrum der Erde sind, der Druck also höher sein müsste. Wie hoch ist der Luftdruck da in mbar durchschnittlich ?

Schließlich müssen sich die Gravitation sich gegenseitig aufheben.

Hallo,

jeder kennt ja das typische Beispiel, dass im Vakuum eine Feder genauso schnell fällt wie ein Hammer, da kein Luftwiederstand vorhanden ist. Ist ja alles soweit schön und gut.

Aber eine Sache frage ich mich immer:

Müsste nicht eigentlich die Feder schneller fallen als der Hammer? Denn die Feder hat ja weniger Masse als der Hammer. Der Hammer würde der Masse der Erde nämlich näher kommen als es die Feder tut. Und Massen, die sich ähnlich sind haben ja auch nicht so eine starke Gravitation zu einander.

Hier ein Beispiel:

Auf dem Mond falle ich langsamer, da die Gravitation dort geringer ist. Das liegt daran, dass ich der Masse des Mondes näher komme. Die Erde wiederum ist viel größer als der Mond. Der Erde komme ich also nicht so nah mit meiner Masse wie beim Mond. Also falle ich dort auch schneller runter.

Mir ist natürlich klar, dass der Unterschied der Masse vom Hammer und der Feder bezogen auf die Erde ein Witz ist. Hier kommt es auf astronomisch kleine Werte an. Aber müsste dann die Feder in der Theorie nicht ein paar millionstel Sekunden (oder noch weniger) früher auf der Erde ankommen als der Hammer?

Weil wenn wir statt dem Hammer sagen wir den Mond nehmen würden, ist es doch klar, dass der Mond nicht ansatzweise so schnell auf die Erde wie die Feder fliegen würde, oder!? Und im Grunde verkörpert der Mond doch das selbe Prinzip wie der Hammer(also in diesem Beispiel natürlich): die Masse ist mehr, als die der Feder!

Könnte es Antigravitationswellen geben auch wenn es keine Teilchen oder Objekte mit einer einer negativen Masse gibt?

Die Gravitationskraft des Mondes bewirkt u.a. die Gezeiten (Ebbe und Flut), da sie aufgrund ihrer Masse eine Anziehungskraft auf die Erde besitzt (wenn auch geringer als die Erde auf den Mond).

Wenn ich mich wiege und wenn ich mich im Gravitationsfeld des Mondes befinde (z.B. bei sichtbaren Vollmond), müsste ich doch eigentlich leichter sein.

Wie hoch ist dieser Effekt bzw. die Kraft, die wirkt.

Angenommen ich wiege im Mondschatten 70kg, wie schwer bin ich dann, wenn der Mond bzw. seine Kraft auf "mich wirkt"?

Wenn der Mond es doch schafft, das Wasser anzuheben (habe etwas von 30cm in Erinnerung), müsste der Effekt doch messbar sein, oder?

Es sollen wohl Quanteninformationen aus einem Schwarzen Loch übertragen werden aber mir erschließt sich nicht die Bedeutung des Anfangs der Nachricht

..-. .-.. ---

Weiß jemand ob es physikalisch sinnvoll anfängt oder der Anfang eine bestimmte Bedeutung z.B. für den Autor des Drehbuchs ect. hat?

Gibt es entdeckte Planeten, auf denen die Zeit sehr langsam vergeht?

Also nicht nur um paar Sekunden, sondern während wir auf der Erde 5 oder mehr Jahre leben, lebt man auf dem anderen Planet nur 1 Jahr. Gibt es so einen Planet?

Oder wie wäre das zum Beispiel in einem anderem Sonnensystem?

Und falls es so einen Planeten geben würde und ich dort 10 Jahre leben würde und dann wieder zurück zur Erde fliegen würde, wäre ich dann doch 200 Jahre alt? Das ist schon krass.

MfG

Ich wurde gefragt was das Gitter darstellen soll bei bilder wo die Gravitation erklärt wird.

Fehlt denn da nicht noch ein Gitter was von oben drauf kommt ?

Und dabei alle dicht an dicht an einem Ort stehen würden ??

Hallo,

man hört ja oft, dass im Vakuum alles gleich schnell fällt, da es dort natürlich keinen Luftwiderstand gibt. Das macht ja alles soweit sinn, aber eine Sache verstehe ich nicht. Eine Bowlingkugel hat ja nämlich viel Masse (was man ja schon an der Schwere merkt), da die Dichte ziemlich hoch ist. Eine Feder hingegen hat viel weniger masse, da sie kleiner ist und eine geringere Dichte hat. Müsste die Feder dann nicht rein theoretisch schneller fallen, als die Bowlingkugel? Als ich meinen Physiklehrer fragte, meinte er, dass das an der Trägheit der Masse liegt. Aber das erklärt doch nicht meine Frage. Die Trägheit ist doch nur darauf bezogen, dass es durch die Luft keinen Widerstand gibt!? Meiner Meinung nach müsste die Feder minimal schneller auf dem Boden ankommen. Natürlich ist mir klar, wie groß das Verhältnis der beiden Gegenständen zur Erde ist. Aber auch wenn die Feder nur 0,000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001 Millisekunden früher auf dem Boden ankommen würde, müsste sie doch schneller als die Bowlingkugel sein!? Schließlich zieht die Erde kleine Massen stärker an als große. Das hat Newton doch schon bewiesen!

Henri Cavendish hat damals behauptet, er hätte die Erde gewogen (er hat den Wert für die Graviationskonstante G gar nicht veröffentlicht, es ging ihm um die Masse M der Erde);

Warum konnte Cavendish das behaupten? Wie kam er zum Wert für die Masse der Erde?

Wenn ein Mensch z.B. eine Masse von 42kg hat, zieht er dann auch die Erde an? Wenn ja, mit welcher Kraft?

Im Vergleich zu einem gleich hohen Gebäude.

Auf dem dem Burjat Dingsbums, dem höchsten Gebäude der Welt in Dubai, müsste man das mit empfindlichen Messgeräten bereits deutlich feststellen können: Steht man auf einem Berg, so ist viel mehr Masse unter einem vorhanden, die gravitationsverstärkend wirken müsste.

Zur Darstellung der Gravitation wird ja häufiger das untere Bild verwendet, in dem das Raum-Zeit Kontinuum dargestellt ist und Gravitation als durch die Masse der sich in ihm befindlichen Objekte "Ausbeulungen" erzeugt.

Zuerst einmal ist das Bild ja vereinfacht, da Gravitation ja in alle Richtungen funktioniert und nicht nur "nach unten". Aber wie breitet sich die Gravitation aus? Denn das Objekt das von der Gravitation beeinflusst wird muss doch irgendeine direkte "Verbindung" mit der Gravitation haben? Als Welle?

Und warum ist die Gravitation so eine schwache Kraft im Vergleich zum Beispiel mit dem Elektromagnetismus? Ich kann hochspringen und habe damit für eine kurze Zeit die Gravitation (also die gesamte Masse der Erde und alles was sich in ihr befindet) überwunden, aber bereits zwei mittel starke Magneten wird kein Mensch voneinander trennen können. Wie kann das sein? Hat die Stringtheorie recht und Gravitation dünstet in andere Dimensionen aus? Was sollen das für Dimensionen sein?

Als ich recherchierte fand ich heraus, dass heute ein Supervollmond kommt. Ich hatte ein Deja-Vu und dachte dass diese Situation schon mal passiert ist.

https://www.t-online.de/leben/familie/id_87648636/pinker-supermond-2020-wann-sie-den-grossen-vollmond-im-april-sehen-koennen.html

Das Zusammenfallen von Erdnähe und Vollmond führt zu Springfluten und maximalen Gezeitenkräften, die auch auf die feste Erdkruste wirken und die rund drei Tage um die Vollmondzeit anhalten.

Denkt ihr dass das irgendwelche Folgen mit sich bringen wird?

Mir war heute ein wenig schwindelig. Liegt das vielleicht an der Kraft der Schwerkraft weil der Mond die Gravitationswellen beeinflusst?