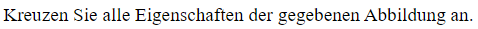Hallo, ich soll obige Ungleichung mittels Induktion unter Verwendung von Euklids Beweis zur Unendlichkeit der Primzahlen zeigen. (Also der Beweis mit dem Produkt aller "endlichen" Primzahlen +1 wobei man dann zeigt, dass dieser Term einen Primteiler hat, der nicht in der endlichen Abzählung vorkommt)
If p_n denotes the n-th prime (in ascending order), deduce by induction from Euclid’s proof of Theorem 1.2 that p_n < exp(2^(n−1)).
Ich habe diese Ungleichung auch bewiesen, aber ehrlich gesagt finde ich meinen Beweis sehr unschön, finde aber keine Verbesserung, auch wenn ich schon mehrere Stunden an der Aufgabe sitze. Mein Beweis per Induktion:
Indunktionsvoraussetzung mit n=1 ist klar. Induktionsannahme auch. Zum Induktionsschluss:
Sei p1,..,pn eine Abzählung der ersten n Primzahlen. Es gilt, dass p1p2..pn+1 einen Primteiler q hat, der noch nicht in dieser Abzählung vorkommt (das ist gerade der Beweis von Euklid zur Unendlichkeit). Da p1,..,pn die ersten n Primzahlen repräsentiert, folgt dass p(n+1) die kleine Primzahl ist, die ein Teiler von p1..pn+1 sein kann (insbesondere kann p1..pn+1 selbst prim sein).
Daraus folgt insgesamt p(n+1)<=p1..pn+1
Nun setze ich die Induktionsvoraussetzung ein und fasse zusammen:
p1..pn + 1 < exp(2^0)exp(2^1)...exp(2^(n-1)) + 1 =
exp(2^0 + 2^1 + ... + 2^(n-1)) +1
Nun erkennt man, dass im Exponenten gerade die geometrische Summe mit x=2 von k=0 bis n-1 steht. Diese Summe entspricht (1-2^n)/(1-2). Das lässt sich vereinfachen zu (2^n - 1 )
Insgesamt folgt bis hierhin:
p(n+1) < 1 + exp(2^n - 1)
Nun zu dem Schritt, der mir selbst absolut nicht gefällt.
Ich zeige, dass das weglassen der +1 vorne und der -1 in der e-Funktion sich so wegheben, dass die ungleichheit erhalten bleibt, also explizit zeige ich dass gilt:
1 + exp(2^n - 1) < exp(2^n) (womit ich fertig wäre)
Ich zeige das so:
1 + exp(2^n - 1) = 1 + exp(2^n)/e = 1/e * (e + exp(2^n))
Es folgt also :
1/e * (e + exp(2^n)) < exp(2^n)
Mit Äquivalenzumformung erhalte ich:
e + exp(2^n) < e * exp(2^n)
Da diese Aussage für n=1 gilt und die Ableitung der e-Funktion die e-Funktion selbst ist, also insbesondere die Ableitung monoton steigt, vergrößert sich der Abstand sogar für alle n>1.
Wie gesagt, dieser letzte Teil gefällt mir gar nicht und ich wäre froh, wenn mir jemand eine alternative und schönere Argumentation bereitstellen könnte.
MfG