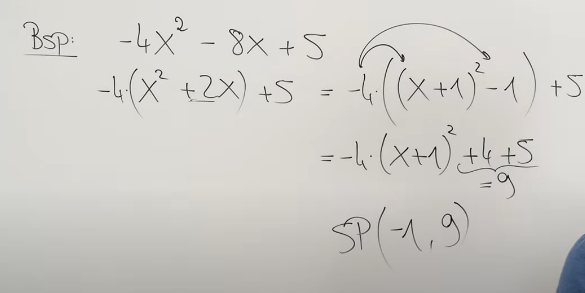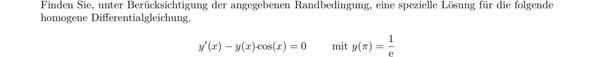Hey, eine kurze Frage zu quadratischen Ergänzungen bzw. Rechenregeln allgemein.
Gegeben sei 3x² - 12x = 36
Nun könnte ich natürlich einfach durch 3 teilen, um den Koeffizienten vor x² zu entfernen. Mal angenommen, ich will dies nicht, und klammere ihn stattdessen aus, um die quadratische Ergänzung anzuwenden.
3(x² - 4x) = 36
3(x - (4/2))² - (-4/2)² = 36
Darf ich an dieser Stelle die 3 wieder mit der Klammer ausmultiplizieren, sodass (3x - (2x - 6)² oder welche Regeln gelten hier? Eigentlich wäre es ja Klammer -> Potenz -> Multiplikation, oder?
Darüber hinaus: Macht es irgendeinen Sinn, den Faktor vor dem x² auszuklammern und nicht gleich durch Teilen zu entfernen, wenn man die Gleichung lösen möchte?
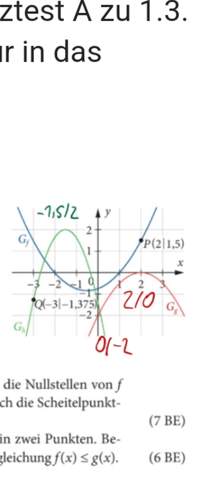
Ich habe die quadratische Ergänzung mithilfe eines Videos zum Scheitelpunkt angeschaut und da man die Gleichung hier nicht vollständig auflösen muss, ist es einfacher, den Faktor auszuklammern. Ich bin mir aber nicht sicher, ob es Fälle gibt, in denen es sinnvoll ist, auf diese Weise eine Gleichung aufzulösen, da ich den Faktor anschließend ja wieder loswerden muss, um meine Lösungsmenge zu erhalten. Was sagt ihr?
So wurde es im Video zum Scheitelpunkt gemacht: