Sksksksksk And I oop,
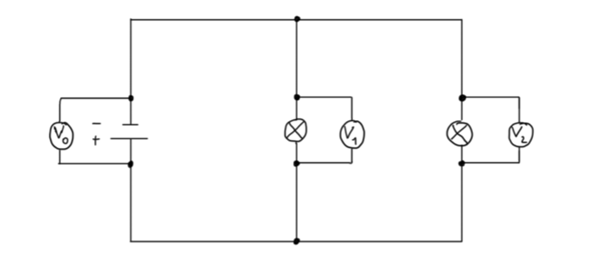
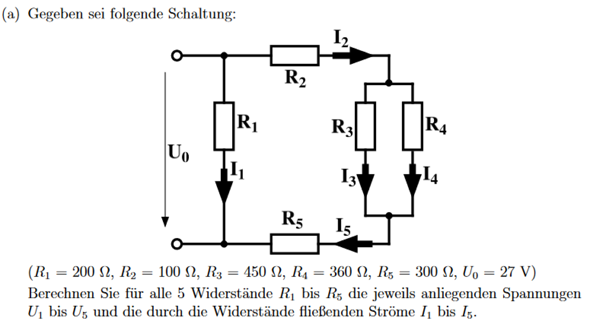
Habe eine kurze dem Strom betreffend bei folgender Schaltung
Wir haben gegen U0 = 27 V, R1 = 200 Ω, R2 = 100 Ω, R3 = 450 Ω, R4 = 360 Ω, R5 = 300 Ω. Gesucht sind U1.... U5, I1... I5
Da die Leitung mit R1 und die Leitung mit R2, R34 und R5 parallel geschaltet sind, ist die Gesamtspannung
R_ges = 200 Ω (100 Ω + 200 Ω + 300 Ω)/ 200 Ω + 100 Ω + 200 Ω + 300 Ω = 150 Ω
Jetzt steht in der Musterlösung.
Masche M1 U1 = U0 = 27 V
Warum ist U0 denn das gleiche wie U1. U0 ist doch gar keine Leitung. Die Spannung kann doch nur U1 sein, oder? Auf jeden Fall folgert man dann
=> I1 = U1/R1 = 27 V / 200 Ω = 0,135 A
Jetzt steht als nächster Punkt
U0 = Rges * Iges => Iges = U0/Rges = 27 V/150 Ω = 0,18 A
Wieso dürfen wir jetzt U0, also U1 gleich Rges * Iges setzen. Da fließt doch nicht die gesamte Spannung, sondern nur U1.
Danach steht in der Lösung
Knoten K2 und K3 = I2 = I34 = I5
Wieso gilt das? Zwischen I2 und I34 sowie I5 sind doch die Widerstände R3 und R4 geschaltet. Da kann doch der Strom nie im Nachleben das Gleiche sein, or?
Der weitere Lösungsverlauf gestaltet sich als nicht weiter kompliziert.
Knoten K1: I_ges = I1 + I2 => I2 = I_ges - 1
I_2 = I_ges - I1 = 0,18 A - 0,135 A = 0,045 A
U2 = R2 * I2 = 100 Ω * 0,045 A = 4,5 V
U5 = R5 * I5 = 300 Ω * 0,045 A = 13,5 V
Jetzt kommt wieder was, was ich nicht verstehe
Masche M2: 0 = I2 R2 + I3 R3 + I5 R5 - I1R1
Warum ist hier der Maschenumlauf gleich null. Und warum wird I3 R3 genommen, aber nicht I3 R4. Die beiden können ja nicht gleich sein, weil ja völlig unterschiedliche Widerstände herrschen. Warm wird I4 R4 nicht in die Masche mitaufgenommen. Der Strom fließt ja auch dadurch.
Die restliche Lösung.
<=> I3 R3 = I1 R1 - I2 R2 - I5 R5 <=> U3 = U1 - U2 * U5
=> U3 = 27 V - 4,5 V - 13,5 V = 9 V
R3 || R4 = U3 = U4 => I4 = U4/R4 = 9V/360 Ω = 0, 025 A
I3 = U3/R3 = 9 V /450 Ω = 0,02 A
U1 = 27 V, U2 = 4,5 V, U3 = 9 V, U4 = 9 V; U5 = 13,5
I1 = 0,135 A; I2 = 0, 045 A; I3 = 0,02 A; I4 = 0,025 A; I5 = 0,045 A
Das kann ich alles nachvollziehen. Nur die fettmarkierten Teile bereiten mir bisschen Nervenflattern. Kann da jemand kurz weiterhelfen?
Mit freundlichem Abstand,