Hey iwie verstehe ich bei folgenden Aufgaben nicht ganz, was von mir erwartet wird, bzw.was der Ansatz ist.
Die Idealisierung einer punktformigen Masse m an einem masselosen
Faden der Länge L wird als mathematisches Pendel bezeichnet.
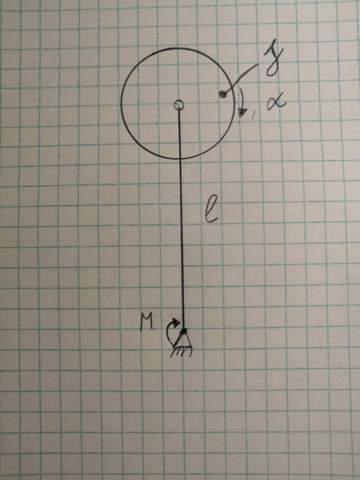
Ein solches Pendel werde, wie in nebenstehender Abbildung gezeigt,
zur Zeit t = 0 um einen kleinen Winkel phi = phi0 aus der Vertikalen
ausgelenkt und losgelasssen. Das Pendel schwinge danach reibungsfrei.
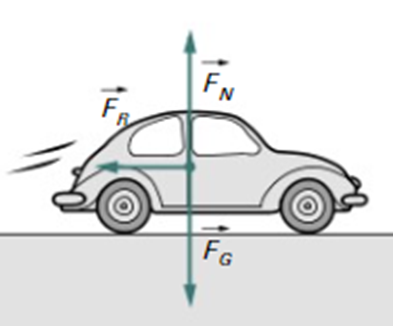
a) Geben Sie die Kräfte an, die auf die Pendelmasse wirken
und zeichnen diese in die Skizze ein. Bestimmen Sie die
Rückstellkraft des Pendels, d.h. die Kraft die das Pendel in die
Gleichgewichtslage zuruckzwingt, als Funktion von ¨phi. Zeichnen
Sie die entsprechende Kräftezerlegung ebenfalls in die
Skizze ein. Fur nicht zu große Auslenkungen kann die
Näherung sin phi = phi benutzt werden. Stellen Sie mit dieser
Näherung eine Bewegungsgleichung für phi(t) auf.
b) Zeigen Sie, dass die harmonische Schwingung,
Phi(t) = A sin (wt + alpha)
diese Bewegungsgleichung fur eine passende Wahl von w erfüllt. Bestimmen Sie aus der Anfangsbedingung phi(0) = phi0 und phi(mit punkt oben drauf)(0) = 0 die Größen A und alpha.
c) Die Winkelgeschwindigkeit w hängt mit der Periode T der Pendelschwingung wie
folgt zusammen:
W=2π/T
Bestimmen Sie die Periodendauer als Funktion der Pendelparameter und der Erdbeschleunigung.
Meine Ideen:
Also das mit den Kräften einzeichnen habe ich hinbekommen und ich hab auch cerschiedene Beziehungen aufgestellt wie Fr= Fg*sin(phi) bzw.Fr=-mg*sin(phi) aber keine Ahnung ob die das wollen für die gleichung der rückstellkraft. Die Kräfte die generell auf die Pendelmasse wirken sind ja Rückstellkraft, Fadenkreuz und Gewichtskraft.Für den zweiten Teil der Kräfteeknteilung hab ich die Gewichtskraft in ihre Komponenten FG tabgebtial zur Kreisbahn und FGn orthogonal zur Kreisbahn zerlegt.wobei ja FGtan der Rückstellkraft entspricht.
Aber nun weiß ich nicht wie ich die Bewegungsgleichung für Phi(t) aufstellen soll. Was ist phie(t) überhaupt? Also wie nann ich denn für einen Winkel eine Bewegungsgleichung aufstellen?
b)hier hab ich absolut keine Agnung was die von mir wollen.was wäre den keine passende Wahl für w?Und wie soll ich A und Alpha bestimmen?