Physik Aufgabe Schwingung?
Muss es nicht ein - sinus sein in Zeichnung weil bei Zeitpunkt t0 ist es doch bei den 4cm in Ruhe und hat keine Beschleunigung?
Und ist die Beschleunigung beim runtergehen negativ? ja oder ? Aber negative Beschleunigung heißt doch dass es gebremst wird, warum hier nicht?

4 Antworten

LG H.

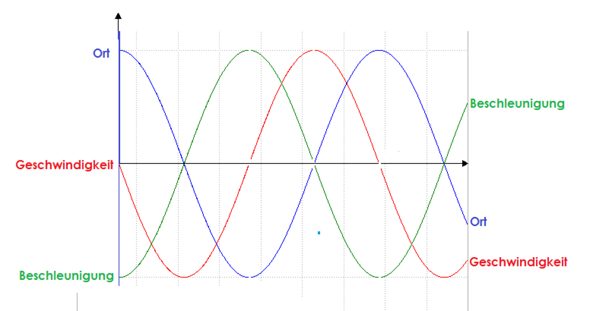
Offenbar geht es um ein senkrechtes Federpendel
- Sinus oder Cosinus ist wurst, es kommt draufan, wie man's betrachtet bzw die Anfangsbedingungen beschreibt.
- Die Anfangsbedingung ist die maximale Auslenkung (Ort, blaue Kurve) oben, wo alles beginnt. Deshalb wird da Cosinus genommen.
- Geschwindigkeit (rote Kurve) beginnt bei null und wird beim Loslassen schnell negativ (nach unten). Mathematisch: erste Ableitung des Orts, deshalb negativer Sinus.
- Da es von oben runtersaust, ist es in der Mitte (Ruhelage) natürlich nicht in Ruhe, sondern in voller Fahrt nach unten (maximale negative Geschwindigkeit, siehe rote Kurve
- Aber die Beschleunigung (grüne Kurve) ist dort in der Mitte null, weil es sich gleichmässig bewegt (weder schneller ncoh langsamer wird)!
- Die Beschleunigung beim Loslassen war Mathematisch: Ableitung der Geschwindigkeit oder zweite Ableitung des Orts, deshalb hier wie in deiner Grafik der negative Cosinus)
- Der unterste Punkt der Schwingung ist dann dort, wo die blaue Kurve das Minimum hat. Dort ist die Geschwindigkeit (rot) null (Totpunkt, wo das Pendel umkehrt), und die Beschleunigung (grün) ist maximal nach oben (weil es grad die Richtung ändert)
- und so weiter.
- Und deshalb sind Ort und Beschleunigung (Kraft) immer entgegengesetzt (rücktreibende Kraft proportional zur Auslenkung), und deshalb die Kurven von Ort und Beschleunigung spiegelverkehrt.

Ob Sinus, Kosinus, -Sinus oder -Kosinus ist egal. Man muss sowieso zum Argument einen Wert addieren (oder substrahieren), damit die Nullstelle bei 0,125 s zu liegen kommt.
Die Richtung der Beschleunigung kann man auch beliebig wählen. (Man muss aber aufschreiben, wierum sie zählt).
Eine negative Beschleunigung bedeutet, dass die (vorzeichenbehaftete) Geschwindigkeit kleiner wird. Wenn sie aber schon negativ ist, dann wird ihr absoluter Betrag größer.
Zeitpunkt t0 ist es doch bei den 4cm in Ruhe
aber die Auslenkung ist nicht null. Eine Auslenkung = sin(0) wäre 0.
Aber negative Beschleunigung heißt doch dass es gebremst wird
nur wenn die Geschwindigkeit positiv ist. Geschwindigkeit ist schließlich ein Vektor, dessen Komponente a negativ sein kann (und dann ist negative Beschleunigung keine Bremsung)
Und das hier ist ein Weg-Zeit-Diagramm, kein Geschwindigkeit-Zeit-Diagramm. Beschleunigungen sieht man hier nicht an der Steigung, sondern an der Krümmung, insofern ist bei t=0 die Beschleunigung positiv, nicht null.
da die Beschleunigung hier anscheinend proportional zur negativen Auslenkung ist, gilt das gleiche. Bei t=0 ist die Beschleunigung dann auch nicht null sondern negativ mit maximalem Betrag. Das ist beim oberen Umkehrpunkt so. Null ist die Beschleunigung beim Nulldurchgang der Auslenkung.
ich habe den Verdacht, hier werden Beschleunigung und Geschwindigkeit verwechselt.
Ok, das ist doch aber ein Beschleunigung-Zeit-Diagramm.
Die nehmen als t0 den Punkt, wo das Handy die maximal Beschleunigung hat, also in der Mitte zwischen der Umkehrpunkte. Aber im Text steht ja, dass t0 beim oberen Umkehrpunkt 4cm ist, also Beschleunigung=0.
Deswegen muss es doch -sinus sein oder nicht?