Physik-Aufgabe zur Feder-Spannenergie richtig gelöst?
Hallo! Ich habe da eine Aufgabe aufbekommen und wollte wissen, ob ich die Aufgabe korrekt gelöst habe bzw. wo der Fehler liegt, da mir das Ergebnis zu klein vorkommt.
Die Aufgabe:
"Eine Schraubfeder wird durch die Kraft F = 0,6 N um s = 3,5 cm gedehnt. Berechnen Sie die Energie, um die Feder weitere 7 cm zu dehnen."
Meine Rechnung:
in latex: (oder siehe Anhang)
\begin{align*}
\text{gegeben:}\\
F &= 0,6 ~ \mathrm{N}\\
s_{1} &= 3,5 ~ \mathrm{cm}\\
s_{2} &= (3,5 + 7) ~ \mathrm{cm} = 10,5 ~ \mathrm{cm}\\
\\
\text{gesucht:}\\
\Delta_{2} E_{\text{pot}} &\text{ in } \mathrm{J}\\
\\
\text{Rechnung:}\\
\text{hookesche Gesetz:} \quad F &=D \cdot \Delta s \quad\mid\quad \div(\Delta s)\\
D &= \frac{F}{\Delta s}\\
D &= \frac{0,6 ~ \mathrm{N}}{s_{2} - s_{1}}\\
D &= \frac{0,6 ~ \mathrm{N}}{10,5 ~ \mathrm{cm} - 3,5 ~ \mathrm{cm}}\\
D &= \frac{0,6 ~ \mathrm{N}}{7 ~ \mathrm{cm}}\\
D &= \frac{0,6 ~ \mathrm{N}}{0,07 ~ \mathrm{m}}\\
D &= \frac{0,6}{0,07} ~ \frac{\mathrm{N}}{\mathrm{m}}\\
D &= 8,57... ~ \frac{\mathrm{N}}{\mathrm{m}}\\
\Delta_{2} E_{\text{pot}} &= E_{pot, ~ s_{2}} - E_{pot, ~ s_{1}}\\
\Delta_{2} E_{\text{pot}} &= \frac{D \cdot s_{2}^{2}}{2} - \frac{D \cdot s_{1}^{2}}{2}\\
\Delta_{2} E_{\text{pot}} &= \frac{D \cdot s_{2}^{2} - D \cdot s_{1}^{2}}{2}\\
\Delta_{2} E_{\text{pot}} &= \frac{D \cdot (s_{2}^{2} - s_{1}^{2})}{2}\\
\Delta_{2} E_{\text{pot}} &= \frac{8,57... ~ \frac{\mathrm{N}}{\mathrm{m}} \cdot (10,5^{2} ~ \mathrm{cm}^{2} - 7,5^{2} ~ \mathrm{cm}^{2})}{2}\\
\Delta_{2} E_{\text{pot}} &= \frac{8,57... ~ \frac{\mathrm{N}}{\mathrm{m}} \cdot 54 ~ \mathrm{cm}^{2}}{2}\\
\Delta_{2} E_{\text{pot}} &= \frac{8,57... ~ \frac{\mathrm{N}}{\mathrm{m}} \cdot 0,0054 ~ \mathrm{m}^{2}}{2}\\
\Delta_{2} E_{\text{pot}} &= \frac{8,57... \cdot 0,0054 ~ \frac{\mathrm{N} \cdot \mathrm{m}^{2}}{\mathrm{m}}}{2}\\
\Delta_{2} E_{\text{pot}} &= \frac{8,57... \cdot 0,0054 ~ \mathrm{N} \cdot \mathrm{m}}{2}\\
\Delta_{2} E_{\text{pot}} &= 0,02... ~ \mathrm{N} \cdot \mathrm{m}\\
\Delta_{2} E_{\text{pot}} &= 0,02... ~ \mathrm{J}\\
\end{align*}
(es lässt mich gerade nicht die Bilder zu den Formeln senden, deswegen nur der Latex-Ausdruck (die Bilder ergänze ich noch))
Kommentar:
Die 0,02 Joule als Lösung klingen für mich viel zu klein... Habe ich einen Fehler gemacht? Wenn ja, wo ist der Fehler?
Die Rechnung:

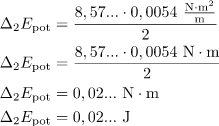
2 Antworten
Sie sagen, dass s_{1} = 3,5 cm groß sei,
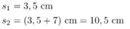
setzen dann aber in der Gleichung s_{1} = 7,5 cm ein.
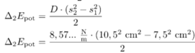
Demzufolge ist der Rest der Rechnung auch nicht gemäß den Angaben korrekt.
Die Federkonstante ist D = F / s_{1} bzw. Delta s ist s_{1} - 0, da diese Kraft F für die Dehnung s_{1} ist, also s_{1} ist schon die Differenz.
Zudem habe Sie beim Latex-Code bei der Differenz der Energien für die Energiekomponenten das "pot" nicht als "\text{pot}", was sie aber davor taten.
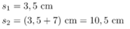
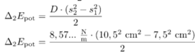
Im ersten Teil zur Berechnung musst du mit dem Wert für Delta s=3,5 rechnen, weil du dafür die angegebene Kraft benötigst. Damit berechnest du die Federkonstante. Erst danach wird um weitere 7cm gedehnt. Da rechnest du dann mit der Energie, die du bis 10,5 gebraucht hast und ziehst die Energie bis 3,5 wieder ab. Müsste zumindest so funktionieren. 🤔
Mit den neuen Werten komme ich auf 0,0084 Joule kommt das hin?
Das weiß ich nicht. Physik im Nebenfach ist bei mir auch ein Semester her. Müssten aber auf jeden Fall kleine Werte sein, weil du ja sowieso schon kleine Werte quadrierst. Würde es also nicht ausschließen.
Und s1 waren auch 3,5 und nicht 7,5 unten, weil du ja eben nicht mit der differenz rechnest.