Radlasten berechnen?
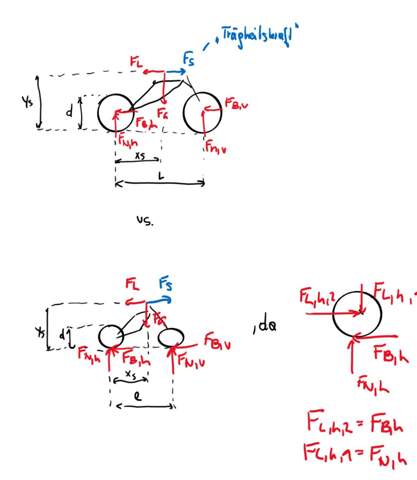
Hi, um Radlasten bei Autos zu berechnen, wird ja meist eine solche Skizze gemacht:
Ich finde, dass das falsch ist. Das würde nur gelten, wenn die Räder komplett starr (ohne Rotation) mit dem Rahmen des Autos verbunden sind. Da sie sich aber drehen, müsste man doch nur Kräfte auf den Rahmen selbst betrachten, dort die Lagerkräfte bei den Radaufhängungen betrachten, und die Räder "ignorieren".
Liege ich damit falsch? Warum wird das (falls ich richtig liege) immer falsch gemacht?
LG
2 Antworten
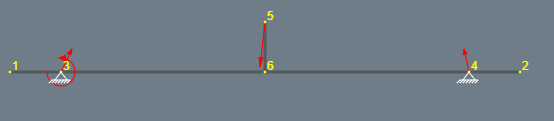
Neue Zeichnung:
Fall (A): Die Radauflagepunkte sind 2-wertige Lager, die x- und y-Kräfte aufnehmen, aber kein Moment
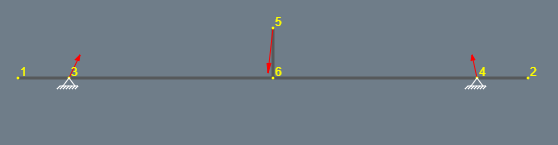
Fall (B): Du gehst nun auf die Radachsen:
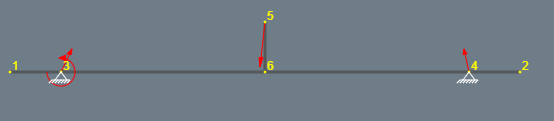
Hier muss die Radnabe ein Moment aufnehmen, welches über die Achse übertragen wird. Die Achse als abstrakter Lagerpunkt muss somit ein Moment aufnehmen. Die "übliche" Annahme, dass Auflager keine Moment aufnehmen, ist hier nicht gerechtfertigt. Stell dir vor, du müsstest das mit der Hand halten - dann würde es sich durchdrehen, wenn du kein Gegenmoment aufwändest.
Merkst Du nun, was du falsch gemacht hast? Du hast dieses Moment scheinbar nicht berücksichtigt - oder etwa doch?
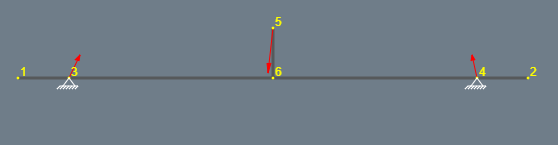
Ich glaube damit den Fehler gefunden zu haben. Du hast recht, das habe ich übersehen. Falls ich dennoch auf Probleme stoße - oder ich das doch nicht übersehen hab, würde ich mich nochmal kurz melden (lasse die Frage daher noch unbeantwortet und setze später den Haken!
Vielen Dank
Es ist egal, wo du freischneidest, die Summe aller Kräfte und Momente im betrachteten System muss immer Null ergeben. Daraus ergeben sich die Schnittkräfte.
Oder hab ich deine Frage falsch verstanden?
Bewegungsgleichung...wofür? Was ist dein konkretes Problem?
Um die Dynamik des Systems zu berücksichtigen (Scheinkräfte etc) Wenn Luftreibung wirkt, so ist das System ja nicht mehr statisch.
Was ist das konkrete Problem? Vielleicht können wir darüber diskutieren oder ich (oder wer anderer) schau mir das an. Einfach nur so "Dynamik" und "Scheinkräfte" ist so weiträumig; da könnte es genau so um Himmelsmechanik gehen, oder um die Dynamik eines Verbrennunsmotors.
Ich hoffe das hat hier Platz. Fahrrad: Gewichtskraft FG, Rollreibungsmoment an den Rädern, Bremsmomente an den Rädern, Luftreibung im Schwerpunkt. Wie viel % der Gewichtskraft wirkt als Normalkraft zwischen Hinterrad und Untergrund? Wenn ich die Trägheitsmomente der Räder vernachlässige, sind die Lagerkräfte (in x und y Richtung) bei den Rädern genau gleich der Normalkraft Fn,h (hinten) zwischen Reifen und Untergrund und der Reibungskraft FB,h zwischen Reifen und Untergrund. Nun hätte ich eben die Radlastverteilung durch Summe aller Kräfte, Summer aller Drehmomente bestimmt, wobei ich die Kräfte Fnh und Fbh an der Achse angreifen lasse. Jetzt kommt für die Achslast blöderweise etwas anderes heraus, als würde ich die Kräfte Fn,h und Fb,h am Berührpunkt zwischen Reifen und Untergrund angreifen lassen (ja logisch, die Abstände sind ja anders). Da die Kräfte am Untergrund und in den Lagern aber betragsmäßig ident sind, ist das doch komisch. Je nach Art der Betrachtung ergeben sich also verschiedene Radlasten.
mach eine Skizze...ich muss jetzt mal raus. aber später schau ich es mir gerne an- oder halt wer anderer.
Skizze ist oben dran. Wär total super, ich verzweifle. Aber ist es nicht grundlegend von der Überlegung her Falsch das so wie beim ursprünglichen Link zu machen (weil sich das Rad eben dreht).
Wenn man die Momente um den Schwerpunkt betrachtet, ergeben sich 2 beinahe identische Gleichungen. Nur einmal ist der Hebel für die Kräfte F_B,n und F_B,v gerade (ys-d/2) statt ys. Also ergeben sich verschiedene Achslasten
>Jetzt kommt für die Achslast blöderweise etwas anderes heraus, als würde ich die Kräfte Fn,h und Fb,h am Berührpunkt zwischen Reifen und Untergrund angreifen lassen (ja logisch, die Abstände sind ja anders).
Da musst du dich verrechnet haben - es muss beide Male das selbe rauskommen
aber sieh dir die Skizze an. Sie ist bis auf den (einmal) anderen Abstand ident!
Du schreibst ja selbst:
F(L, h, 1) = F(N, h)
...
Das muss so sein (Trägheitsmoment mal außen vor).
Wo siehst du konkret eine Diskrepanz?
Reifenmasse? Wenn das Trägheitsmoment vernachlässigt wird kann man das guten Gewissens auch vernachlässigen. Ich glaube auch nicht, dass es dadurch dann passt.
Ich kann mir nur vorstellen, dass der "oft gemachte" Ansatz falsch ist...
Hast du Reifenmasse Null angenommen? Und auf beide Arten gerechnet? Und es kommt was unterschiedliches raus? Oder was genau? Ich kann ja nicht wissen, wo du das konkrete Problem siehst.Welcher Ansatz?
Ich habe die Reifenmasse als Null angenommen. Wenn ich mit Reifenmasse rechne, dann kommt dennoch etwas anderes heraus.
Nein, Reifenmasse 0 zeigt ja gerade die Situation in der Skizze. :/
da muss das selbe rauskommen. geht ja mechanisch nicht anders ;-)
Deswegen suche ich auch den Fehler bei dem Ganzen :D
Fang mal einfach an: kommt auch was anderes raus, wenn du die Reibungskräfte Null setzt?
Nein, dann würde dasselbe herauskommen. Die Reibungskräfte multiplizieren sich mit einem Term ys-d/2 im Fall der oberen Skizze und ys im Fall der unteren.
Ich meine wenn du komplett ohne Radreibung rechnest. Dann kann sich ja nichts multiplizieren, wenn es schon Null ist.
Achso, d.h. wenn du die Reibung Null setzt, kommt das selbe raus?
Ja, ist klar. Ich meinte, in der Formel mit Radreibung kommt das mit den Termen vor. Wenn ich die Reibungen 0 setze fallen diese "einzigen" Unterschiede in der Formel raus.
Wie lässt du die Reibungen eingehen, wenn du an den Achsen schneidest?
Du musst ja auf jeden Fall bedenken, dass die Reibungen vorne und hinten, also F(B,v) und F(B,h) i.A. verschieden sind, außer es wirkt keine Antriebskraft am Hinterrad,
Wie meinst du? Ist das nicht in der Bemerkung rechts der Skizze klar?
Du hast G, FL und FS.
Die Reibkraft am Vorderrrad ist
F(B,v) = μ*F(N,v)
Lässt du diese Beziehung auch eingehen, wenn du an der Achse rechnest?
Die Reibkraft am Hinterrad ist damit determiniert.
Ich habe es bisher nur als F(B,v) geschrieben, da sich µ in Abhängigkeit vom Schlupf ändert. Es geht in weiterer Folge nämlich auch darum, die maximale Kraft F(B,v) zu bestimmen, bevor ein Rad etwa durchdreht o.ä.
aber du hast recht, das hängt zusammen. Dennoch, würde sich nichts dran ändern, dass verschiedene Lösungen herauskommen.
Die beiden Fälle - ich versuch sie mal zu beschreiben:
A) Du rechnest mit den Auflagerkräften am Boden und nimmst die Reibungskräfte willkürlich an.
Summe aller Kräfte = 0
Summe aller Drehmomente = 0
Da kommt dann irgendwas raus für die Kräfte
B)
Du rechnest mit den Lagerreaktionen an den Achsen (so wie im rechten Bild) und nimmst die Reibungskräfte willkürlich an.
Summe aller Kräfte = 0
Summe aller Drehmomente = 0
Da kommt dann irgendwas raus für die Lagerreaktionen.
Aber vorsicht:
Die Achse des Hinterrads ist hier ein dreiwertiges Lager, da es ja auch ein Drehmoment aufnimmt. An diesem Lager gilt nicht Summe aller Momente ist Null, da du ja in die Pedale (Kette) trittst. Und sobald du irgend eine Form von Reibung hast, MUSST du in die Pedale treten. Es geht sich sonst mit dem Kräftegleichgewicht nicht aus.
Ist das vielleicht dein Fehler? Du musst auch aufpassen bei den Reibungskräften: diese gehen beim Vorderrad etngegen der Bewegungsrichtung und beim Hinterrad nach vorne, sodaß eine Resultierende nach vorne übrigbleibt.
Ja genau so - super Beschreibung. Also die Vorzeichen der Reibungskräfte ändern nichts an meinem Problem.
Wie meinst du das mit dreiwertig? Im Fall das gebremst wird ergibt sich (bei schlupffreiem Bremsen) direkt das Gegenmoment durch die Reibungskraft am Untergrund oder nicht? Dann ist man wieder Momentenfrei. Das ist ja mehr oder weniger der Grund, weshalb das Trägheitsmoment vernachlässigt wurde - damit diese Überlegung keine Rolle spielt. Und zum Antrieben eines masselosen Rades braucht man eben kein Drehmoment.
Kannst du mir das etwas genauer erklären? Wenn ich daher komme, dass ich zunächst für alle Bauteile (Räder, Rahmen) Bewegungsgleichungen aufschreibe, scheint mir das etwas uneinsichtig. Eine Kraft zwischen Boden und Rad würde doch das Rad drehen. Oder?