Binomialverteilung – die besten Beiträge

Guten Tag,

a habe ich ohne Probleme beendigt. Jedoch bin ich mir bei n unsicher, wie jetzt genau die Tabelle aussehen soll. Ich habe noch nie mit so einer Tabelle gearbeitet. Wie genau muss hier die Tabelle aussehen? Danke

Hallo

Warum schreibt man beim Binomialkoeffizienten in den Nenner noch zusätzlich (n-k)! ?

Würde nicht k! reichen?

Danke!

Wir machen gerade Binomialverteilung und ich kenne mich bei einem Beispiel nicht ganz aus: Es geht darum, wie hoch die Wahrscheinlichkeit ist, dass man bei acht Würfen maximal einen 6er würfelt. Ist die Gegenwahrscheinlichkeit dann mit genau zwei 6ern? Normalerweise würde ich das so machen, aber beim vorherigen Beispiel waren 2 6er die Gegenwahrscheinlichkeit, jetzt kommt es mir irgendwie unlogisch vor.

Hallo, leider habe ich Schwierigkeiten diese Aufgabe zur Binomialverteilung zu lösen. Wie müsste man hier denn vorgehen?

Formulieren Sie ein Zufallsexperiment und ein Ereignis, dessen Wahrscheinlichkeit mithilfe des Terms

(15 nCr 4) •0,25⁴ • 0,75¹¹ berechnet werden kann.

LG

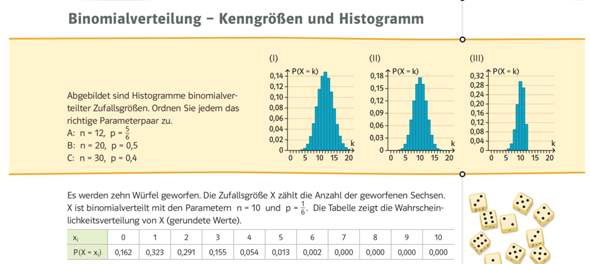
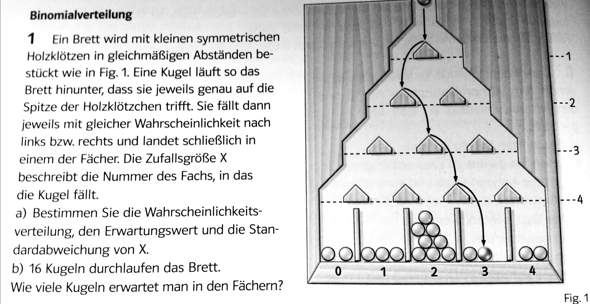
Ein Hersteller füllt Suppenpulver in Gläser ab. Die Füllmenge ist annähernd normalverteilt mit dem Erwartungswert mu = 125, 1g und der Stan dardabweichung sigma = 0, 58g

Veranschaulichen Sie alle folgenden Berechnungen anhand einer Skizze der Dichtefunktion:

a) Berechnen Sie die Wahrscheinlichkeit, dass ein zufällig ausgewähltes Glas eine Füll menge von i. mindestens 125g, ii. weniger als 125g aufweist.

b) Berechnen Sie die Wahrscheinlichkeit, dass die Füllmenge eines zufällig ausgewählten Glases um mehr als 1% vom Erwartungswert abweicht.

c) Berechnen Sie die Wahrscheinlichkeit, dass ein zufällig ausgewähltes Glas eine Füll menge zwischen 124,5g und 126g aufweist. d) Berechnen Sie diejenige Füllmenge, die von 95% aller Gläser nicht unterschritten wird.

A und c habe ich berechnet. A)56,84% & 43,15% , c) 78,91%

Wie berechnet man b Ich würde für b jetzt 125,1*0.01 (für 1%) rechnen... es sollte 0.0310 herauskommen...

Ich wäre euch echt dankbar für eure hilfe :)

Ich komme bei dieser Aufgabe nicht zurecht.

Aufgabe:
Multiple-Choice-Tests werden für einfache Leistungsüberprüfungenverwendet. In nebenstehendem Test gibt es fünf Fragen mit jeweils vier Antwortmöglichkeiten, von denen eine richtig ist.

Die Note „ausreichend" wird erteilt, wenn zwei Antworten richtig sind.

Die Note „befriedigend" gibt es für drei richtige Antworten, bei vier richtigen gibt es ein „gut" und bei fünf richtigen ein sehr gut".

Vermutlich müssen Sie die Antworten meistens raten.

Mit welcher Wahrscheinlichkeit werden Sie

a) die Note „sehr gut" bekommen?

b) die Note „gut" bekommen?

c) die Note „befriedigend" bekommen?

d) die Note „ausreichend" bekommen?

e) den Test nicht bestehen, also weniger als zwei Antworten richtig haben?

Was ist mein n,k,p und q? Ich bin leicht verwirrt. Ist mein n 4 oder 5? Die Formel ist mir bekannt.

Im vergangenen Monat wurden beim Straßenverkehrsamt einer Stadt 5239 Fahrzeuge angemeldet, darunter 1774 eines bestimmten Herstellers. In den ersten 2 Tagen dieses Monats wurden 449 Fahrzeuge angemeldet. Bei welcher Zahl von Fahrzeugen des betreffenden Herstellers würde man sagen, dass sich der Anteil der Neuzulassungen geändert hat? (a =5%)

Danke im Voraus

Hey! Kann mir jemand bei der Aufg. d) helfen. C) ist gelöst, aber den Sachzusammenhang von d) verstehe ich nicht.

Aufg: In einer kleinen Töpferei nimmt beim Brennen in der Regel einer von fünf Töpfen Schaden.

c) Berechnen Sie die Wahrscheinlichkeit, dass bei einer "Mini-Produktion" von 7 Töpfen keiner, einer, zwei, drei, etc. schadhaft sind.

d) Bestimmen Sie die Anzahl schadhafter Töpfe, die bei einer Sicherheitswahrscheinlichkeit von 82% bei der Mini-Produktion aus c) zu erwarten sind.

Keine Idee.

Herzlichen Dank im Voraus!

Hallo gemeinsam,

wie ich in den vorherigen, gestellten Fragen erwähnt habe, liegt mir Stochastik nicht nahe. Hierbei habe ich eine Frage, und zwar verstehe ich nicht, wie ich mithilfe der Binomialverteilung ein Histogramm zeichnen soll und wie ich überhaupt auf diese Werte bzw. Wahrscheinlichkeiten kommen kann. Ich hatte sonst nie Probleme mit dem zeichnen von Histogramme.
Zuerst dachte ich, dass man dies mit der Fomel E(x)= n*p ausrechnen kann, aber es kommen andere Ergebnisse raus bzw. ist es der Erwartungswert. Zum Beispiel die Werte aus dem unteren Bild. Wie kommt man auf die Werte der Wahrscheinlichkeiten, also P(X=x1)?
Danke im Voraus, für jegliche Hilfe!!

Hi Leute

ich brächte echt eure Hilfe. Ich war eine Zeit lang in Quarantäne und mir fehlt ein Teil in Mathe. Ich habe mir es teilweise selbst beibringen können. Nun stecke ich bei einem Beispiel fest und kann keinen fragen, weil sie es selbst nicht verstehen. Das Thema ist Wahrscheinlichkeitsrechnung.

In einer Studie wurde erhoben, dass 55% der Bevölkerung Skifahrerinnen sind, die anderen 45% fahren nie Ski.

• Berechnen Sie die Wahrscheinlichkeit, dass von 20 zufällig ausgewählten Personen mehr als 10 Skifahrerinnen sind.

Von den SkifahrerInnen fahren 88% häufig Ski, 12% nur gelegentlich.

• Interpretieren Sie das Ergebnis der Berechnung 0,55 * 0,88 = 0,484 im gegebenen Sachzusammenhang.

Ich verstehe nicht wie ich da anfange. Alles was ich weiß ist, dass ich ein Baumdiagramm wahrscheinlich zeichnen muss.

Die Lösung für die Aufgabe wäre:

• ca. 59,14%
• Wahrscheinlichkeit, dass eine zufällig aus der Gesamtbevölkerung ausgewählte Person häufig Ski fährt.

Eure Hilfe würde mir echt meine Note in Mathematik retten. Deshalb bedanke ich mich jetzt schon einmal an alle im Voraus :)

Kann mir jemand bei c), d) und e) mit dieser kumulativen binominalverteilungsrechnung helfen. Ich soll das mit dieser Stochastik Tabelle lösen und daher auch die entsprechende Schreibweise verwenden. Bei c) z.B wenn man das jetzt normal mit dieser binominalverteilungs-Formel lösen wollen würde..müsste man doch einfach nur n über k weglassen in der Formel oder, da gefragt wird das genau die ersten zehn gezogenen Kugeln weiß sein sollen und nicht irgendwann irgendwelche bei dem 50 mal ziehen.

Hallo!

Kann mir bei dieser Aufgabe bitte jemand helfen? Ich kann leider nicht einordnen, wie ich sie angehen muss.

Vielen Dank im Voraus

Es geht um Nummer 8

Ich verstehe es nicht...............was ist hier die angehensweise bei der letzten Aufgabe mit den kugeln im sack... :(

In einem Säckchen befinden sich 4 rote, 3blaue, UND 5grüne gleichartige Bausteine. Es werden sechs steine mit Zurücklegen entnommen. Berechne die warscheinlichkeit,Dass man mehr als vier grüne Steine zieht.

Wieso zeigt dieses Verteilungsdiagramm keine Binomialverteilung an?

Falls die Antwort lautet, dass die Wahrscheinlichkeiten stetig steigen oder abfallen müssen, wie kann es dann sein, dass das Maximum teilweise bei zwei ks liegt??

danke im Voraus

Was soll ich für P(X=K) im Taschenrechner für K angeben? für P(X<=K) muss man ja einfach nur K angeben.

sind die Lösungen richtig?

LG

brauche Hilfe bei der Nummer 10 komme allein nicht weiter bitte schnell antworten Klausur ist in paar tagen

Guten Tag.

Ich würde gerne um Ihre Hilfe bitten - könnten Sie mir bitte bei folgender Aufgabe helfen?

Gilt immer - gilt nie - es kommt darauf an

c) Binomialkoeffzienten wie (5,3) = (5 * 4 * 3)/(1 * 2 * 3) berechnet man als Brüche. Sie brauchen deswegen nicht ganzzahlig sein.

→ ? k. A.

e) In jeder Zeile des Pascal-Dreiecks findet man Gleichheiten der Form (5,2) = (5,3).

→ ? k. A.

Vielen Dank!