5 Hühner legen 20 Eier in 8 Tagen. In wie vielen Tagen legen 37 Hühner 761 Eier? Runde auf ganze Tage.

Guten Abend, kann mir jemand bei den folgenden Aufgaben helfen bzw. einen Rechenweg aufstellen? Mein Mathebuch und Googeln haben mir bis jetzt leider noch nicht weitergeholfen und ich bin mittlerweile echt am Verzweifeln :(

Die (Text)Aufgaben lauten wie folgt:

Ein Lokführer eines Zuges erkennt an einem Vorsignal, dass er seinen Zug vor dem bevorstehenden Hauptsignal zum Anhalten bringen muss. Das Hauptsignal ist 1000m entfernt.

Nach Einleiten des Bremsvorgangs legt der Zug in t Sekunden den Weg s(t)=30t - 0,4t² (in Metern) mit einer Geschwindigkeit von v(t)=30 - 0,8t (in Metern pro Sekunde) bis zum Stillstand zurück.

1. Berechnen Sie den Zeitpunkt t, bei welchem der Zug steht. Endet der Bremsvorgang vor dem Hauptsignal?

2. Die Zahl 30 in den Funktionsgleichungen steht für die Geschwindigkeit des Zuges in Metern pro Sekunde, die der Zug vor dem Bremsvorgang hat. Berechnen Sie wie hoch diese Geschwindigkeit maximal sein darf, damit der Zug noch rechtzeitig zum Stillstand kommt.

Hallo, ich sitze gerade an dieser Aufgabe und bin mir unsicher.

Muss man von g und f jeweils das unbestimmte Integral bilden oder die Differenzemfunktion und dan das bestimmte Integral. Vielleicht kann mir ja jemand helfen.

Danke

Es geht um die Teilaufgabe b). Ich war nun so mit einem anderen Thema beschäftigt und komme gerade einfach nicht darauf.. die Lösung sagt t=1/500.

Vielen Dank im Voraus. :)

In einer Vase befinden sich 12 rote, 24 weiße, 15 grüne , 21 gelbe , 30 blaue und 18 schwarze Kugeln. Es werden zwei Kugeln nacheinander gezogen, wobei die erste gezogene Kugel wieder zurückgelegt wird.

Mit welcher Wahrscheinlichkeit hat man zwei Kugeln gleicher Farbe gezogen?

Ein Glücksrad hat 30 gleich große Felder, die von 1-30 beschriftet sind.

Wie groß ist die Wahrscheinlichkeit, bei zwei Drehungen

a)jedes Mal eine durch 10 teilbare Zahl zu erhalten?

b)eine Summe kleiner als 5 zu erzielen?

Ist das so richtig? Wenn nein könntet ihr mir weiterhelfen?

lieben Dank!

I

Bei einem Puzzle mit 6708 Teilen ist die Anzahl der Teile in jeder Reihe größer als 40 und kleiner als 50. Wie viele Teile liegen in einer Reihe?
Erläutere dein Vorgehen.

Meine Frage ist, wie komme ich auf die Lösung ohne alles durchzurechnen?!

Aufgabe 5:

Am Ende eines stressigen Arbeitstages gönnt sich Herr Schneider ein Bad. Nach dem Ziehen des Stöpsels fließen 15 l/min aus der 135 | Badewanne.

a) Bestimme die Funktionsgleichung für den restlichen Badewanneninhalt. Zeit (in Minuten) → Badewanneninhalt (in Liter)

b.) Berechne, wie viel Wasser ist nach 3,5 min noch in der Badewanne ist.

c) Berechne, wie lange das Wasser schon läuft, wenn in der Badewanne 60 I sind.

d) Berechne, nach welcher Zeit die Badewanne halb leer ist.

e) Berechne, wie lange es dauert bis die Badewanne leer ist.

kann mir bitte bitte jemand helfen

Hallo Ihr Lieben.

Ich brauche dringend Hilfe bei der Aufgabe 3 und 4 ich würde mich sehr über Hilfe freuen dankere

Ich schreib morgen eine Prüfung und ich hab keine Ahnung wie Aufgabe 6,8 und 9 berechnet wird.hab leider keinen der mir hilft deshalb ein fettes danke wer mir erklären würde wie ich das berechnen soll

Heyy ich hab mir für Teilaufgabe b) überlegt, dass man ja einfach die Gleichung f (x) mit 1 gleichsetzen muss, um die Aufgabe zu lösen oder? Leider schaff ich es ned die zu lösen, hat jemand eine Idee? Vielen Dank und liebe Grüße :)

Hallo liebe Community, könnt ihr mir helfen bei der Fehlerberichtigung. Ich habe meiner Meinung nach alles richtig gerechnet aber es sollen Fehler darunter sein.

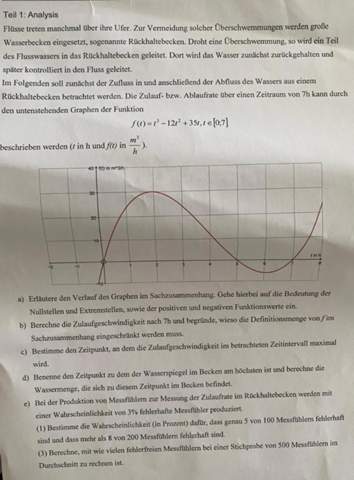
a) Die positiven Funktionswerte geben die Zufflussgeschwindigkeit des Wassers in dem  Rückhaltebecken an. Die negativen Funktionswerte hingegen geben eine Abflussgeschwindigkeit an, beziehungsweise wie schnell das Wasser aus dem Rückhaltebecken abfließt. 

Die Zuflussgeschwindigkeit steigt an und erreicht nach 2h ihr Maximum, dort ist die Zuflussgeschwindigkeit am größten. Von da an, wird die Zuflussgeschwindigkeit immer geringer bis t=5h.  Dort ist der Wasserstand am größten. Von nun an wird Wasser abgepumpt bis t=7h. Bei t=5h und t=7h ist die Zuflussgeschwindigkeit des Wassers null. An der Stelle t=5h beginnt der Übergang von Zufluss zu Abfluss. Im Zeitraum von (5:7) ist die Zuflussgeschwindigkeit negativ. Im Sachzusammenhang bedeutet das, dass Wasser wieder  in einen Fluss geleitet wird. 

Dabei wird von der Abflussgeschwindigkeit gesprochen.

b) 

f(7)=0. (Zuflussgeschwindigkeit ist null)

Im Sachzusammenhang macht es Sinn den Definitionsbereich einzuschränken, weil laut der Funktion f die Funktion für

t->unendlich = unendlich. Das würde bedeutet, dass die Zuflussgeschwindigkeit unendlich groß wird. Im Sachzusammenhang ist es nicht möglich die Zuflussgeschwindigkeit bis unendlich zu beschleunigen, aus diesem Grund macht es Sinn den Definitionsbereich einzuschränken.

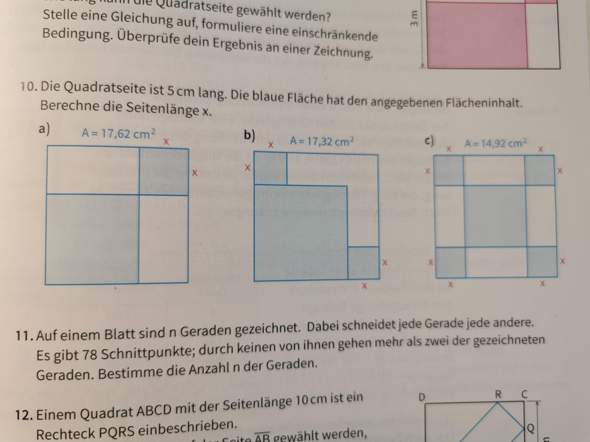
c) Extremstelle von f

—> Xe=1,92h

d) (Hochpunkt der Stammfunktion) von f. Bei t=5h ist der Wasserstand am größten, weil bis zu diesem Zeitpunkt immer mehr Wasser in das Becken gepumpt worden ist. Um zu berechnen wie hoch der Wasserstand zu diesem Zeitpunkt ist, berechnet man 

F(5)=93,75m^3

e)(1)

5/100= 5% die Wahrscheinlichkeit beträgt 5%

—> 0.05*200= 10

10>8 die Bedingung ist erfüllt ( mehr als 8 Fühler sind kaputt)

(2) 0,03*500=15

500-15=485 

Im Durchschnitt kann man bei einer Stichprobe von 500 mit 485 fehlerfreien Messfühlern rechnen.

Wie lautet der Wert von a+b+c, wenn:

• a⋅b=2
• b⋅c=24
• c⋅a=3
• Eine der Zahlen ist ein Bruch.
• Alle drei Zahlen sind positive Zahlen.

Heinz und Franz wollen die Pacht der Gruft ihrer gemeinsamen Vorfahren verlängern und Instandhalten. Sie besichtigen die Gruft. Franz zahlt 263 € mit seiner EC-Karte für die Verlängerung der Pacht im Rathaus. Heinz zahlt in bar

dem Betreuer der Gruft 130 €. Heinz und Franz einigen sich darauf, jeweils die Hälfte der Gesamtkosten zu übernehmen. Wieviel Geld muss Heinz an Franz überweisen, damit jeder genau die Hälfte der Gesamtkosten trägt ?

philipp verkauft eine maxi-pizza für 7,80€. Für den strassenverkauf will er mini-pizzen mit halbem durchmesser herstellen. Wie viel müsste eine mini-Pizza kosten damit man genauso viel für sein geld bekommt?

Ein Kfz-Mechaniker benötigt zum Wechseln eines Reifens 2 Arbeitsschritte. Um den alten Reifen zu entfernen, benötigt er 8 Minuten. Um den neuen Reifen aufzuschrauben, benötigt er 7 Minuten. An einem Tag müssen die Reifen von 24 Autos gewechselt werden. Wie viel schneller wären die Reifen gewechselt, wenn anstatt 4 Kfz-Mechanikern 6 Kfz-Mechaniker gleichzeitig arbeiten würden und der fünfte und sechste Mechaniker eine Stunde früher anfangen würden?

Ein Hotel mit abzählbar unendlich vielen Zimmern ( eines für jede natürliche Zahl) ist immer voll besetzt und niemand entscheidet sich zu verreisen. Es ist dennoch immer möglich Platz für einen zusätzlichen gast zu finden, indem jeder vorhandene Gast aufgefordert wird in das Zimmer mit der nächsthöheren Nummer zu ziehen. So kann der neue Gast Zimmer 1 belegen.

a) Es werden nun keine weiteren Gäste aufgenommen und die Gäste entscheiden sich jede Nacht in ein neues Zimmer zu ziehen. Können die Gäste jede Nacht das Zimmer wechseln, ohne jemals dasselbe zu belegen wenn das Hotel eine Strikte Regel hat, dass jedes Zimmer in jeder Nacht besetzt sein muss?

b) Es wurden abzählbar unendlich viele neue Stockwerke hinzugefügt und nun soll in den zuvor vorhandenen Zimmern ein unendliches Buffetrestaurant eingerichtet werden, sodass alle Gäste aus ihren alten Zimmern in die neuen Zimmer in den oberen Stockwerken umziehen müssen. Wie lässt sich jedem Gast ein neues Zimmer zuweisen, ohne dass ein Zimmer in den oberen Stockwerken leer steht?

Ich sitze schon ne weile an dieser Aufgabe und brauche Hilfe

Meine gedanken soweit:

a) hätte gedacht nein, weil wenn alle ein zimmer weitergehen mussder "letzte" zuruck in zimmer 1, damit dieses belegt ist, dies geschieht immer wieder bis der Gast, welcher bei Zimmer 1 startet wieder bei Zimmer 1 ankommt.

b) kann man nicht einfach sagen das der Gast in Zimmer 1 in das erste Zimmer im oberen Stockwerk zieht, der Gast in Zimmer 2 dann in das zweite? oder vertehe ich hier irgendetwas nicht

danke schon einmal

Hallo,

Weiß jemand die Antwort auf diese Aufgabe? LG

Paula und Jonas erkunden das neue skigebiet. "hier fahre ich nicht. das ist mir viel zu langweilig. die Piste hat maximal 15% gefälle", stellt Jonas fest. paula meint: "dann fahr doch gegenüber, dort gibt es bis zu 115% gefälle." Jonas lacht:" mehr als senkrecht geht ja wohl nicht." Was meinst du dazu?

Hallo, Frage steht oben

Nebenbei weiß jemand was die Volumenformel für die Kugel ist?:)

Ich hatte heute eine Mathepepfung. Ein Textbeispiel hat mir den Kopf zerbrochen. Ich würde gerne wissen, ob jemand die Aufgabe lösen kann. Mich interressiert es sehr, ob ich bei der Prüfung richtig gelegen habe.

Rechenaufgabe:

24 kinder benötigen 70 killo brot für 14 tage

Wie viel Tage benötigen 36 kinder mit 90 killo brot?

Die Kinder der 5c-Klasse laufen den Wald. Der Sporttrainer hat eine Strecke von 1000 Metern gemessen. Platziert einen roten Kegel am Anfang und am Ende. Außerdem stellt sie alle 100 Meter einen roten Kegel auf. Wie viele kegel braucht er?

Sollte Aufgaben berichtigen die ich falsch gemacht habe, würde gerne die Lösungen wissen da ich leider nicht weiter komme

Die Frage hatte ich heute bei einem Einstellungstest am Computer.
Meine Antwort war 16 (100m2= 10x10m

pro 10m passen 4 Zäune auf eine Seite, 4Seiten= 4x4=16 Pfosten).

Ich bin mir aber sicher, dass die Antwort falsch ist. Welchen Denkfehler mache ich?

Wie soll ich das berechnen bzw. wie soll ich das machen?
ich hab jeweils das Volumen der 3 Zylinder berechnet und zusammen addiert

das Volumen der äußeren beiden Zylinder ist jeweils 220,89 und von der Stange in der Mitte 196,34 das hab ich dann addiert und die Hantel hat insgesamt ein Volumen von 638,12

638,12 mal 7,83 ergibt 4996,47 Gramm was mach ich damit ? Wieso wiegt meine 2kg Hantel fasst 5kg das versteh ich nicht



Hallo ihr Lieben,

kann mir jemand bei dieser Matheaufgabe helfen?

Ich bedanke mich im Voraus:)

Nachdem die Firma A schon 210 Stunden an einem Projekt gearbeitet hat kommt die Firma B für den Rest zur Hilfe. Zusammen erledigen sie den Rest in 126 Stunden. Die Firma B hätte alleine für den gesamten Auftrag 210 Stunden länger als Firma A. Wie lange brauchen die Firmen A und B jeweils einzeln für die gesamte Arbeit.

Bitte gesamten Rechnungsweg (Gleichung) aufzeigen. DANKE.

Hallo, ich habe zum Thema Bruchgleichungen eine Textaufgabe bekommen die ich nicht verstehe, kann mir bitte jemand helfen sie zu lösen ?

Danke schonmals

Hallo in der schule haben wir diese Textaufgabe über bruchgleichungen bekommen jedoch verstehe ich diese nicht, kann da jemand helfen ?

Sara hat 15 Sms mehr verschickt als Timon. Hätten beide je nur ein Fünftel ihrer Sms verschickt, so hätte Timon die hälfte der Anzahl Sms von Sara verschickt. Wie viele Sms haben die beiden verschickt ?

Danke Schonmal.

Kann mir jemand helfen wie man bei Nummer 310 b und c löst

Kann mir jmd erklären wie ich a) und b) machen soll? Vor allem hab ich Probleme mit a ich hab so etwa noch nie gezeichnet und bräuchte Hilfe

möchte sicherstellen

Moin,

kann mir wer kurz bei dieser Textaufgabe helfen die Formel zu finden:

Eine Zeitung hat für den Druck ihrer Auflage zwei Druckpressen zur Verfügung. Die grosse Presse schafft die Arbeit in vier Stunden. Beide Pressen brauchen zusammen 2,4 Stunden. Wie viele Stunden braucht die kleine Presse allein für die Arbeit?

Gruss

Frage: In die Tanzschule komme heute dreimal so viele Mädchen wie Jungen, so dass es nur 6 Paare aus je einem Mädchen und einem Jungen gibt. Wie viele Mädchen haben keinen Tanzpartner?

Antwort: 12

Ist meine Antwort richtig?

Hallo ich hab eine Textaufgabe , weiß leider nicht wie ich sie lösen soll. Ein Kapital von 20.000€ wird mit einem Zinssatz von 5% jährlich verzinst.
a) Vor wie vielen Jahren betrug das Kapital bei gleichem Zinssatz 15.000€

b) In welchem Jahr nimmt das Kapital erstmal um 5000€ zu?

Also ich muss so nh Aufgabe lösen und checke es nicht. Kann mir da jemand vielleicht weiterhelfen? Dankeschön!

Aufgabe: Das Schaufelrad eines Riesenbaggers zum Braunkohleabbau besteht aus 12 je 3 m langen Schaufeln, die dicht an dicht stehen und den Umfang bilden.

1. Welchen Durchmesser hat das Rad?
2. Wie viel Erde wird in 10 Umdrehungen abgetragen, wenn jede Schaufel durchschnittlich 6 m? Erde fasst?

Kann mir bitte jemand helfen?

Danke

Hallo ihr Lieben,

zur folgenden Textaufgabe hätte ich eine Frage:

Aufgabe:

Ein älterer PC würde zur Lösung einer bestimmten Aufgabe 6 Stunden, ein anderer, neuerer für dieselbe Aufgabe 4 Stunden benötigen. Wann ist die Aufgabe gelöst, wenn beide PC unabhängig voneinander an der Aufgabe arbeiten können, der langsamere zunächst 1 Stunde alleine rechnet und dann beide zusammen die Aufgabe fertig lösen?

Ich hatte 2 als Lösung, und bin davon von folgender Gleichung ausgegangen:

1/6x+1/4x=5/6 (da ja der ältere PC 1h bereits gerechnet hat, sind nur noch 5/6 der Aufgabe zu erledigen).

Laut Lösungsbuch soll da aber 3 rauskommen. Übersehe ich etwas in der Aufgabenstellung?

Danke im Voraus!

EIn 20 Euro Schein wird in 1 Euro Stücke und 50 Cent Stücke umgewandelt.Die Anzahl der 1 Euro stücke ist um 5 größer als die der 50 Cent Stücke.Wie viele Geldstücke erhält man von jeder Sorte?

1.Gleichungssystem mit 2 Variablen aufstellen

2.Lösungsmenge bestimmen

Sowas wird wahrscheinlich in meiner Arbeit drankommen aber ich habe keine ahnung wie das geht kann es mir wer erklären?

Hallo,

ich habe heute eine Mathearbeit geschrieben und wollte fragen, dass wenn man zwei Textaufgaben von ungefähr 5 Stück vermasselt hat, man trotzdem noch eine 2 als Note erreicht. Ich weiß, die Frage ist jetzt sehr pauschal, aber ich mach mir viele Gedanken gerade drum , der Lehrer hatte leider keine Punkte angegeben aber ich denke mal 5 pro Stück.

Hallo,

ich habe eine HA bis morgen und wir machen LGS also das Lineare Gleichungssystem. Aber ich weiß bei der Aufgabe 3 nicht wie das funktioniert. Man bekommt ja zwei Gleichungen raus mit denen man rechnen kann. Ich kann aber keine Gleichungen aufstellen. Kann mir bitte jemand helfen. Aufgabe 3 Ist die Aufgabe.

Bild:

Aufgabe 3

Eine quadratische Spanplatte hat einen Umfang von 352 cm. Die Platte wird an allen Schmalflächen (Kanten) mit einem Umleimer versehen, der eine Materialstärke von 7 mm hat und an den Enden auf Gehrung geschnitten wird.

- Berechne die Gesamtlänge des Umleimers in Meter.

Ich stehe total auf dem schlauch. Ich habe 352+(8*7) gerechnet. Laut Lehrer jedoch falsch. Morgen schreib ich eine Klausur und würde gerne den Lösungsansatz verstehen.

Es were wirklich sehr lieb wenn sie mir es erklären bzw die Lösung sagen könnten

Zimmer 5,00 m lang, 4,20 breit

Baumarkt: Ein Paket mit 8 Paneelen kostet 9.90€ jedes Panel ist 1,40m lang und 20 cm breit

wie viele Rollen muss ich kaufen?

wie viel Geld gebe ich dafür aus?

Aufgabe 2

Und das Zimmer ist 3,05 m hoch Im Baumarkt gibt es Raufaserrolen die 10 m lang und 50 cm breit sind jede Rolle kostet 7,85

wie viele Rollen muss ich kaufen?

wie viel Geld gebe ich dafür aus?

danke schon mal im Vorraus

Hallo,

Bei der Texgaufgabe geht es darum, dass die Inflationsrate 2% beträgt und es wird gefragt, wie lange es dauert, bis 2000€ nur noch die Kaufkraft von 1000€ hätte.

Mein Ansatz wäre 2000€ × 0.98 hoch x, ist das richtig?

Hallo, ich brauche Hilfe bei der Aufgabe:

Herr Schulz kauft sich eine Telefonkarte mit 50,00 EUR Guthaben für sein Handy. Der durchschnittliche Minutenpreis beträgt 0,80 EUR

1. Bestimmen Sie mit Hilfe dieser Daten eine lineare Funktionsgleichung.
2. Wann hat Herr Schulz sein Guthaben zur Hälfte aufgebraucht?
3. Wieviel Minuten kann Herr Schulz insgesamt mit seinem Guthaben telefonieren?

1kg Brot kostet 1,80€. Wieviel kosten 200g

Guten Tag,

es geht um folgende Aufgabe:

60 Prozent aller Menschen trinken Kaffee. 45% Prozent trinken Tee und 18 Prozent trinken weder Kaffee noch Tee.Wie viel Prozent aller Menschen trinken sowohl Kaffee als auch Tee?

Wäre nett, wenn mir das jemand erklären könnte.

Guten Abend zusammen,

ich habe eine Frage bezüglich des Ablaufes einer Aufgabe bei der Vektorrechnung.

Es geht sich um eine quadratische Pyramide mit den Punkten A(0|0|0), B(0|8|0), C(8|0|0), D(8|8|0) und die Spitze S(4|4|10). Eine Längeneinheit entspricht einem Zentimeter.

Nun wird die Pyramide in ein 4cm hohes Becken mit Wasser gelegt. Es soll das neue Volumen der Pyramide berechnet werden welches NICHT im Wasser liegt.

Ich wäre so vorgegangen:

Geradengleichung von jedem Punkt zur Spitze der Pyramide erstellen.

Dabei jeweiligen Punkt als Ortsvektor nehmen.

Dann bei jeder Geraden die x_3-Koordiante gleich 4 setzen und nach der Unbekannten auflösen per Äquivalenzumformung. Bei mir kommt dann 4/10 heraus für jede Gerade. Dann 4/10 für die Variable in der Geradengleichung einsetzen und man erhält den neuen Punkt in der Höhe von 4cm.

Und danach mit den neuen Punkten und gleichbleibenden Koordinaten für die Spitze das neue Volumen ausrechnen. (Beispielsweise per Kreuzprodukt).

Ist mein Rechenweg so in Ordnung oder habe ich irgendetwas übersehen bzw. bin ich das Problem völlig falsch angegangen?

Ich würde mich sehr über eure Antworten freuen.

Schöne Grüße

RuhrpottNiklas

HI Leute, ich versuche meinen kleinen Bruder zu helfen da er leider bei den beiden Textfragen nicht weiterkommt, leider weiß ich es auch nicht ,ich habe paar Ideen aber so richtig verstehen tue ich es auch nicht.

Ich danke im voraus.

Ausgabenstellung:

Ein Radfahrer tritt gegen einen Motorradrollerfahrer an und erzielt durchschnittlich 40 km/h. Der Motorroller erreicht im Mittel 70 km/h und startet eine halbe Stunde nach dem Radfahrer.

• Wie viel Strecke haben die beiden jeweils zurückgelegte, wenn sie sich treffen?

Antwortmöglichkeiten:

● ungefähr 82,67 km

● 70 km

● ungefähr 46,67 km

● 40 km

*Ich bröuche Hilfe beim Rechenweg, also wie ihr auf welche Lösung gekommen seit*

DANKE

Sue hat sechs Karten: zwei sind blau, eine ist rot und drei sind weiß. Sie spielz ein Spiel in dem ein sechseitiger würfel geworfen wird und eine farbige karte wird zufällig gezogen.

wie wahrscheinlich ist es eine rote karte zu ziehen und eine gerade ziffer auf dem würfel zu haben?

bitte entschuldigt den text, den hab ich aus dem englischen übersetzt. Ich weiß dass die wahrscheinlichkeit für die karte 1/6 ist und die für den würfel 3/6, aber wie rechne ich das zusammen???

Mit drei Druckern desselben Typs können 270 Seiten in siebeneinhalb Minuten ausgedruckt werden.

Wie lange dauert das Drucken von 210 Seiten, wenn ein Drucker nicht funktioniert?

Hey, ich habe hier eine Logikaufgabe gefunden und hab auch die Lösung, ich habe jedoch keinen geeigneten Rechenweg gefunden, um es zu erklären.

Hier habe ich eine Matheaufgabe, die ich nicht verstehe. Mein Lehrer hat mir gesagt, ich darf nur x benutzen. Kein y!!!!! Dies ist eine Aufgabe mit Gleichungen.

In einer Tombola sind 1000 Lose. Der Anteil an Gewinnen beträgt 5%. Wie viele Nieten muss man aus der Tombola entfernen, um eine Gewinnchance von 20% zu erhalten?

Heute Leute, schreibe morgen in Mathe eine Klausur zum Thema Lineare Funktionen. Ich hab eine Arbeitsblatt erhalten und bin bis zur 3 Aufgaben angekommen, die ich leider nicht so richtig verstehen. Ich hoffe Ihr könnt mir dabei helfen.

Vielen Dank im Voraus !

Kann mir bitte jemand die Lösungen sagen ?😊

Ich verstehe eine Aufgabe nicht, sie lautet:

In einem Restaurant gibt es 4er Tische und 8er Tische. An den totalen 14 Tischen gibt es insgesamt 72 Plätze. Berechnen Die die Anzahl 4er Tische.

Für die volle Punktzahl wird eine Gleichung verlangt.

Hallo, ich bräuchte Hilfe bei einer Aufgabe in Mathe. Ich habe bereits meinen Lehrer gefragt aber es trotzdem nicht so richtig verstanden. Vielleicht kann mir jemand erklären, wie ich die e) lösen kann? Danke im Voraus!

Ich muss heute diese drei Textaufgaben lösen und verstehe sie irgendwie nicht so recht, es wäre sehr lieb wenn mir jemand helfen könnte sie zu verstehen und mir sagen kann wie ich sie am besten lösen kann.

Danke!!

Ist die a und b so richtig gerade bei b bin ich mir nicht sicher?

Ich komme hier leider nicht weiter. Ich habe vieles ausprobiert, bin aber noch nicht ans Ziel gekommen.

Folgende Aufgabe:

Herr Landwehr hat einen Kredit über 100 000€ bei seiner Bank aufgenommen. Da er für die Finanzierung seines Neubau weitere 60 000€ benötigt, leiht ihm die Bank diese zu einem 5% höheren Zinssatz. Nach einem Jahr muss Herr Landwehr insgesamt 15 500€ Zinsen an die Bank bezahlen. Berechne Die beiden Zinssätze pro Jahr für die Kredite!

Schonmal im Vorfeld ganz vielen Dank für die Antwort.

ich verstehe den Bruch nicht. Wieso ?

Tim hat einen neuen Bausatz bekommen und möchte damit einen Kran bauen. Dazu müssen zwei Lochschien in rechten Winkel miteinander vschraubt und stabilisiert werden. die Löcher in den Schienen haben einen Abstand von einem Zentimeter. Das verschrauben ist ganz einfach. Für das stabilisieren hat er zwei verschiedenen Länge Lochschienen zur Verfügung.

Entscheide, welche Lochschiene er verwenden kann und gib an, wo sie angeschraubt werden muss?

Problem/Ansatz:

Anzahl der Löcher geeignet? Lochkombinatio

6                Ja        s3w3 oder s4w3

10

18

Danke für die Hilfe 😀

Verstehe nicht, wie ich diese Aufgabe lösen sollte?

Kann jemand mir dabei helfen es geht um Lineare Gleichungssysteme

Zwei Zuleitungen füllen zusammen ein Gefäss, wenn die erste 6 h lang geöffnet ist und die zweite 4 h lang. Verwechselt man die Öffnungszeiten, so läuft ein Sechstel des Gefässinhaltes über. Welchen Bruchteil des Gefässinhaltes liefert jede Leitung pro Stunde? In wie vielen Stunden wird das Gefäss durch jede Leitung einzeln gefüllt, in wie vielen durch beide zusammen? 

Kann mir jemand das lösen?

Riesenkängurus können bis zu 10 m weitund 3 m hoch springen. Die Sprungbahn isteine Parabel.

a) Bestimme die Gleichung einer Parabelfür einen 10 m weiten und 3 m hohenSprung. Lege hierzu zunächst die Koordinaten des Scheitelpunktes fest.

b) Prüfe rechnerisch, ob ein Riesenkänguru über einen Kleinbus von 2m Breite und2,50 m Höhe springen kann.

Hallo,

Wie könnte man bei diesen Aufgaben vorgehen ?

Verstehe die beiden Aufgaben überhaupt nicht. Habe keinen blassen schimmer. Man muss doch mit der pq Formel rechnen. Aber wie? Wäre sehr nett wenn jemand mir die beiden aufgaben erklären könnte. :)

Kann sich jemand die Aufgabe a) anschauen und sagen, ob ich richtig berechnet habe und richtig erklärt habe („Vergleichen Sie“)?

Außerdem komme ich bei der b) nicht auf den Lösungsansatz.

Ich sitze seit Tagen an dieser Nummer, komme aber nicht weiter, wie man das lösen soll.
Hat vielleicht von euch jemand einen Lösungsweg ?

Danke schonmal im Voraus.

Hallo zusammen,

iIn der Arbeit gab es eine Textaufgabe die Ich nicht lösen konnte:

Für ein Jugendtreffen werden insgesamt 12 Zelte aufgebaut. Es werden nur Zelte für drei Personen und Zelte für 4 Personen verwendet. In den 3-Personen-Zelten schlafen die Mädchen in den 4 Personen Zelten die Jungen. 43 Jugendliche belegen alle Plätze.

1: Wie viele Jungen und Mädchen gibt es jeweils?

2: Wie viele Zelte müssen noch angeschafften werden wenn zu diesen 43 noch 12 hinzukommen und die Zeltbelegung gleich bleibt?

Es währe nett, wenn mir jemand einen Lösungsweg mit Hilfe der 4 Rechenverfahren reinschreiben könnte ;)

a.)Bei welchem Zinssatz erhält man 18 € Jahreszinsen für ein Guthaben von 720€ ?

b.) Auf welchen Betrag wächst ein Guthaben von 2000 € bei einem Zinssatz von 5% in einem Jahr an? Nun lässt man das Guthaben mit den erhaltenen Zinsen auf dem Konto. Wie viel Geld hat man dann nach einem weiteren Jahr.

die dichte eines atomkerns beträgt ca. 2 × 10¹⁴kg/dm³. Gib die Masse eines Würfels mit V= 1cm³ an, der nur aus Kernmaterial besteht!

Die Lösung der aufgabe lautet: m~2×10¹¹kg aber ich versteh nicht, wie man darauf kommt

1. Der Flächeninhalt des weißen Kreuzes der dänischen Flagge beträgt ein Viertel der Gesamtfläche. Wie breit wird der weiße Streifen bei einer Flaggengröße von 3 m auf 5 m?
2. Bei einer anderen dänischen Flagge mit demselben Längenverhältnis ist der weiße Streifen 1 m breit. Berechnen Sie die Maße.

Aufgabe 1 habe ich die Gleichung 5x + 3x -x^2 = 15/4 dann ist x = 0,5.

Aber wie berechne ich die Aufgabe 2? Kann mir da jemand weiterhelfen?

LG

Hallo,

Ich bin gerade dabei Steckbriefaufgaben zu bearbeiten. Aber irgendwie komme ich nicht weiter. Wir sollen Aufgabe 2 bis 4 machen. Aufgabe 2 habe ich schon gemacht, da bin ich mir aber sehr sicher, dass das falsch ist. Und bei Aufgabe 4 finde keine fünfte Gleichung, die ich aufstellen kann.

Würde mich sehr freuen, wenn mir das jemand erklären könnte. Danke!

Mit Erklärung bitte. Bin dankbar für jede Hilfe!

Habe mir schon den Kopf darüber zerbrochen und komme einfach nicht zu einem vernünftigen Ergebnis.

Ihr würdet mir sehr helfen!!!

Eine Dachkonstruktion besteht aus sichelförmigen Trägern, deren Begrenzungslinien Parabeln sind.
a) Stelle die Funktionsgleichung der Parabel auf.

b) Welche Breite hat der Träger 4m vom Rand entfernt?

Einbeck und Northeim sind 20 km voneinander entfernt. von Einbeck fährt Tim um 10 Uhr in die Richtung Northeim mit der Geschwindigkeit 20 kmh .von Northeim aus radelt Lotta in Richtung Einbeck mit der Geschwindigkeit 18 kmh. beide treffen sich an einer Stelle die 5 km von Einbeck entfernt ist. wann ist Lotta in Northeim abgefahren, wie lange ist Lotta gefahren wie lange Tim?

Hallo, kann mir jemand erklären wie ich diese Aufgabe berechne, bitte mit Formeln, ich habe im Internet zu dieser Aufgabe zwar mehrere Beiträge gefunden und weiss auch das Ergebnis, hab aber keine Ahnung wie man das ausrechnet, bzw was überhaupt gesucht wird, Prozentwert, Grundwert oder Prozentsatz, ausserdem weiss ich nicht ob es ein verminderter oder vermehrter Grundwert ist und ob ich es demnach anders ausrechnen muss. Wäre sehr nett wenn mir das jemand anschaulich erklären könnte. Wie gesagt das Ergebnis ist mir bekannt ich habe aber keinen Plan wie man das ausrechnet und finde im Internet auch nirgends einen Rechenweg, den ich verstehe.

Hey, ich verzweifele total mit linearen Funktionen, ich habe diese Textaufgabe aufbekommen die ich dann vortragen muss

kann mir vielleicht jemand helfen??

ich danke im vorraus!

In einer Spielzeugkiste liegen 60 gleiche Bauklötze. Die Kiste und die Klötze wiegen zusammen 4 Kilo. Wenn die Kiste gefüllt ist so fasst sie 110 Klötze. Dann wiegen die Kiste und die Klötze zusammen 6 Kilo.

a.) Wie schwer ist ein Bauklotz?

b.) Wie schwer ist die leere Kiste?

C.) Stelle den Zusammenhang zwischen Anzahl Klötze ( =x ) und dem Gesamtgewicht ( =y ) in einem Koordinatensystem dar und notiere die Gleichung.

Hier musste ich als erstes berechnen wie viel Gramm Plätzchen im Sonderangebot verkauft werden.

Eine Tüte mit 125 g Plätzchen kostet bisher 1,49 €. Ein Supermarkt wirbt mit dem folgenden Plakat

Sonderangebot: 125 g + 20 % mehr Inhalt für nur 1,89 €

und das war mein Ergebnis: Der Grundwert ist 125g. Davon berechnest du 120%, also 125g x 1,2 = 150g

aber ich kann nicht feststellen ob es jetzt zum vergleich günstiger ist?

kann dass bitte jemand begründen?

Einen Tunnel von 1,159km Länge soll alle 30,5 m eine Lampe erhalten. Wie viele Lampen werden benötigt,wenn an den Einfahrten die je 1Lampe angebracht wird?

Kann jemand für mich diese Textaufgabe lösen?:

Eine 20 cm große Kerze, die pro Minute 0,5 cm abbrennt und eine 15 cm große Kerze, die pro Minute 0,2 cm abbrennt, werden gleichzeitig angezündet. Wann sind die Kerzen gleich groß und wie groß sind sie dann? Stelle für beide Kerzen eine Funktionsgleichung auf und löse rechnerisch (nicht als Tabelle oder Graph

Danke

Halloo, ich hab gerade das Thema Ähnlichkeiten in Mathe und soll die Höhe eines Turmes bestimmen, wo die Turmspitze mit einem 3,95m langen stab angepeilt wird. Das erste Männchen was zuerkennen ist, ist 1,70m groß und hält einen Abstand von 4m zu einem zweiten Männchen das den besagten Stab hält, dieses zweite Männchen mit dem Stab hält einen Abstand von 136m zum Turm. Könnte mir jemand vielleicht helfen das zu berechnen?

Ich verzweifle bis ins Mark. Wie rechne ich? Ist dort ein rechter Winkel? Warum weshalb? Bitte hilft mir BITTE

Ich brauche die Loreleyaufgabe

Nina macht ein Praktikum in einer Bäckerei. Für eine Feier mit 140 Gästen werden Schokoladenkuchen und Cake-Pops bestellt. Der Bäcker hat Bleche mit den Maßen 400 mm • 600 mm. Aus einem Blech Schokoladenkuchen kann man genau 30 Stücke schneiden. 

a.) Der Bäcker rechnet mit 40% Gewinn. Gib eine Empfehlung für den Preis eines Stücks Kuchen.

b.) Einige Gäste der Feier achten auf ihre Ernährung und wollen wissen, wie viele Kilokalorien ein Stück Kuchen hat. Gib ihnen Auskunft.

c.)* Zusätzlich sollen 420 Cake-Pops gebacken werden. Ein Cake-Pop hat einen Durchmesser von 3 cm. Nina hat berechnet, dass zwei 3-l-Schüsseln Teig dazu ausreichen. Überprüfe.

Ein Zylinder ist 32 cm hoch. Wie hoch ist ein Kegel mit gleichem Radius, der dasselbe Volumen wie der Zylinder hat? Begründe deine Antwort!