Hallo,
mich beschäftigt eine dringende Frage:
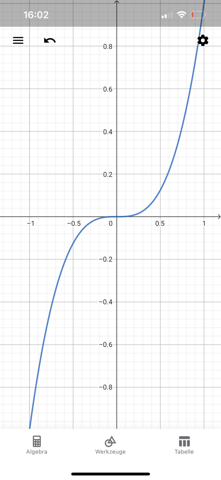
Die Funktion f(x)=x^5 besitzt ja im Punkt P(0/0) eine Nullstelle. Optisch gesehen befindet sich hier ein Wendepunkt. Der Graph hat an dieser Stelle eine fünffache Nullstelle und wenn man weiß, wie der Graph aussieht, dann weiß man auch, dass sich die Krümmung im Ursprung von einer Rechts- in eine Linkskurve umwandelt. Also sollte dort folglich ein Wendepunkt sein.
Nun aber der Haken:
Die Bedinung für einen Wendepunkt ist, dass die 2. Ableitung 0 ist, dass f''(x)=0 und f'''(x)≠0 ist.
Dies ist bei f(x)=x^5 aber nicht der Fall (also Optisch gesehen, ist hier ja ein Wendepunkt im Ursprung, aber die Bedingung für einen Wendepunkt ist nicht erfüllt):
f'(x)=5x^4
f''(x)=20x^3
f'''(x)=60x^2
Wenn ich 0 in f''(x) und f'''(x) einsetze, komme ich auf Folgendes Ergebnis:
f''(x)=20*0^3=0
f'''(x)=60*0^2=0
Bei der zweiten Ableitung kommt 0 raus. Soweit passt es noch. Bei der dritten Ableitung kommt allerdings ebenfalls 0 raus :O. Die Bedingung, für einen Wendepunkt ist allerdings, dass die dritte Ableitung UNGLEICH 0 ist. Was hat das zu bedeuten? Heißt das, f(x)=x^5 hat doch keinen Wendepunkt im Ursprung? Aber die Krümmung ändert dort doch ihr Verhalten, also muss es doch ein Wendepunkt sein. Oder etwa nicht?
Hat zufällig jemand eine Erklärung für dieses Paradoxon? :O
Die Frage geht mir einfach nicht mehr aus dem Kopf...
Vielen Dank im Vorraus für eure Erklärungen :)
PS: Unser Lehrer wusste auch keine Antwort auf die Frage :O