Stimmen diese Aussagen und wieso lautet die Antwort so?
Ich brauche das für diese zwei Aussagen:
a) Wenn der Graph von f‘ in einem Intervall I oberhalb der x-Achse verläuft, dann ist f in diesem Intervall streng monoton steigend.
b) Wenn die Ableitung f‘ einer Funktion f in einem Intervall streng monoton steigend ist, dann ist auch f in diesem Intervall streng monoton steigend.
2 Antworten
a ist Richtig, weil du dir das Monotonieverhalten von f(x) durch f'(x) herleiten kannst. Ab dem Intervall, wo f'(x) oberhalb der X-Achse liegt, ist f(x) streng monoton steigend. liegt ein Teil von f'(x) unterhalb der X-Achse, ist der Graph von f(x) in dem Intervall streng monoton fallend.
b ist falsch, denn das muss nicht immer sein. Sehen wir uns dazu einfach dieses Bild an.
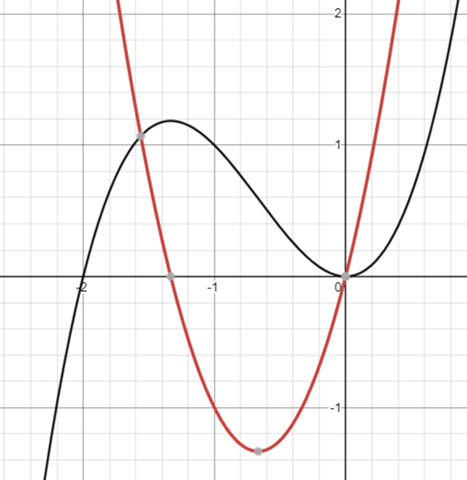
der schwarze graph ist f(x), der rote f'(x). Ab x = -4/3 ist f'(x) streng monoton steigend, f(x) ist ab x = -4/3 aber noch streng monoton fallend.
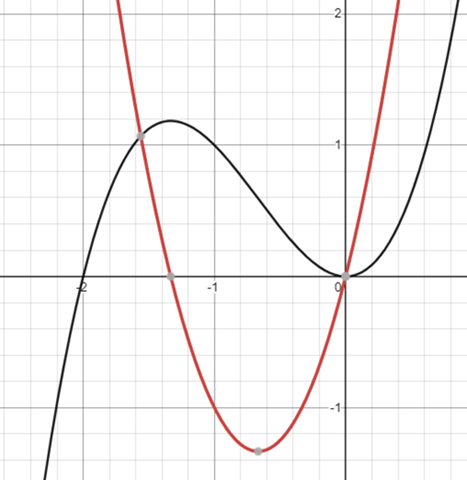
:D, btw hab nen kleinen Fehler entdeckt. für b sind es nicht x = -4/3 sondern x=-2/3
Nr 1) stimmt auf jeden Fall.
Nr 2) stimmt nicht m.E.
Echt lieb von dir, vielen Dank!