In welchem Intervall ist die Funktion monoton fallend/steigend?
Hi
Ich hab ein wenig Probleme Funktionen auf Monotonie zu untersuchen.
Gegeben ist folgende Funktion:
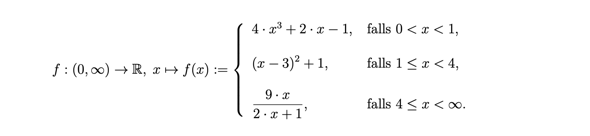
Nun soll ich das Intervall (0, ∞) zerlegen in Intervalle, in denen die Funktion f monoton wachsend bzw. monoton fallend ist.
Ich überlege schon die ganze Zeit aber komme irgendwie nicht weiter. Ich hab leider auch keinen Ansatz gefunden.
Könnte mir bitte jemand weiter helfen. Wäre super. Vielen Dank
2 Antworten
Monotonieverhalten untersuchst du mit Hilfe der 1. und der 2. (um Maximum und Minimum zu suchen) Ableitung.
Ist die 1. Ableitung im Intervall größer als Null, ist die Funktion da streng monoton wachsend. Bei größer gleich Null monoton wachsend.
Analog für streng monoton fallend und monoton fallend.
Die Ableitung 12x²+2 der ersten Funktion ist im angegebenen
Intervall > 0, die Funktion ist dort also streng monoton steigend.
Achsoo okay, also setze ich quasi in die Ableitung 12x^2 +2 Werte im vomIntervall 0<x<1 ein (zB 0,5). Da kommen dann immer Werte >0 raus. Also ist die Funktion streng monoton steigend?
Genau, wenn die Steigung immer >0 ist, geht es nur aufwärts ;-)
Danke, das hat mir echt geholfen!! Wenn ich jetzt nur noch die Nullstellen angeben muss, wie mach ich das dann? kannst du mir da noch kurz helfen? weil f'(x)=12·x^2 +2 hat ja keine Nullstellen?
Du berechnest f'(x) für die anderen Intervalle. Angenommen im 2. Intervall ist die 1. Ableitung kleiner gleich 0, also der Graph monoton fallend, weißt du, dass bei x=1 eine Nullstelle der 1. Ableitung sein muss, also dort ein lokales Maximum ist. Achtung: Das was ich grad geschrieben habe, ist nur ein Beispiel. Ich habe gerade nichts durchgerechnet :)
Bilde die Ableitung und schau, wo sie komplett >= 0 oder <= 0 ist.
Okay danke👍. Wenn ich richtig verstanden habe: Bei der ersten Funktion 4·x^3 +2·x−1 bilde ich ganz normal die erste Ableitung. Setze sie gleich 0 und berechne die Nullstellen. Diese setze ich die Nullstellen in die zweite Ableitung ein. Soweit verstehe ich es auch. Aber dann schaue ich mir das Intervall 0<x<1 an und ziehe dann welchen Schluss? irgendwie blick ich da noch nicht wirklich durch..:/