Hey, ist diese Funktion streng monoton steigend?

Hey, ist diese Funktion (f(x)=x^3) streng monoton steigend, oder nur monoton steigend?:

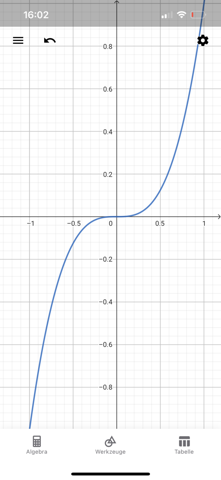
Vielen Dank.

Answer 1

[tunik123]

Sie ist streng monoton steigend, obwohl an einer Stelle der Anstieg 0 ist.

Maßgebend ist, dass für Argumente x1 und x2 mit x1 < x2 die Funktionswerte f(x1) < f(x2) sind.

Comments

[Arian88]

Ja, aber ist doch trotzdem an einer Stelle kurz Null und ist es dann noch nur monoton steigend?

[tunik123]

@Arian88

Das stört nicht, denn in der Definition wird von verschiedenen x1 und x2 ausgegangen. Und die können nicht beide gleichzeitig 0 sein.

Bei x1 = 0 und x1 < x2 ist x2 > 0 und f(x2) > 0. Also f(x1) < f(x2) = 0.

Bei x2 = 0 und x1 < x2 ist x1 < 0 und f(x1) < 0. Also f(x1) < f(x2) = 0.

Also in jedem Falle steng monoton steigend.

[Rammstein53]

@Arian88

Der Funktionswert spielt keine Rolle. Entscheidend ist die Bedingung in der Antwort.

[Arian88]

@tunik123

Achso, es geht also nicht darum, wenn kurz 0 ist (bei den X-Werten)? A

[tunik123]

@Rammstein53

Ich wollte das nur am Beispiel f(x) = x³ erklären. Da ist es schön einfach ;-)

Natürlich können Horizontalwendepunkte (Sattelpunkte) sonstwo liegen. Es muss weder x noch f(x) dort 0 sein.

[Arian88]

@tunik123

Ich könnte rein theoretisch auch zwei Intervalle erstellen, oder?:

I1: -~;0= streng monoton steigend

I2:0;+~= streng monoton steigend

Dies wäre auch korrekt, oder?

[tunik123]

@Arian88

Wenn die Funktion stetig ist, kann man das so machen. Es ist aber trotzdem nicht schön, denn die betrachteten Argumente x1 und x2 können ja in verschiedenen Intervallen liegen. (Ich musste erstmal überlegen, ob es eine Ausnahme gibt, habe aber keine gefunden.)

[Arian88]

@tunik123

Ja, ich müsste eben eine sogenannte Monotonietablelle anlegen und und die einzelnen Intervalle und dessen Monotonieverhalten bestimmen. Dann wäre dies korrekt, oder?

[tunik123]

@Arian88

Ja.

Kann man machen, muss man aber nicht 😉

Answer 2

[evtldocha]

Ja, das ist sie (f'(x) = 3x² ≥ 0 für alle x ∈ ℝ)

Comments

[tunik123]

f'(x) ≥ 0 ist nicht hinreichend für strenge Monotonie.

f'(x) darf nur in (maximal) einem Punkt = 0 sein.

[Arian88]

Ja, was denn nun von beiden Möglichkeiten?

[evtldocha]

@Arian88

Was soll denn dieser Kommentar? Wenn Du das Kriterium nicht kennst, musst Du ja nun nicht gleich "Was denn nun" nachfragen, so als ob hier ein Widerspruch stünde oder zwei Möglichkeiten genannt seien.

Answer 3

[Rhenane]

streng monoton steigend: das "streng" fällt nur weg, wenn mindestens 2 Punkte nebeneinander denselben Funktionswert haben.

Comments

[Arian88]

Okay, auch wenn es für kurze Zeit Null ist?

[Rhenane]

@Arian88

in den Definitionen liest Du etwas in dieser Art: streng motonon steigend wenn gilt: f(x2)>f(x1) mit x2>x1. Das bedeutet: wenn Du beliebige Stellen x1 und x2 nimmst, also auch direkt benachbarte, dann ist eine Funktion streng monoton, wenn bei diesen (benachbarten) Stellen der "rechts liegende" Funktionswert größer ist (bzw. kleiner bei fallenden Funktionen). Das streng fällt weg, wenn gilt x2>x1 und f(x2)>=f(x1). D. h. sind benachbarte Funktionswerte gleich (was bei ganzrationalen Funktionen nie der Fall ist), dann fällt das Wörtchen "streng" weg.

Wenn Du Dir hier den Nullpunkt anschaust, dann ist der Fukntionswert links davon kleiner und recht davon größer, d. h. von links nach rechts geht es "Punkt für Punkt" immer nach oben.

Answer 4

[lilie404]

Ja, ist sie, für jedes x>y auch f(x)>f(y) gilt. Also die Funktionswerte immer ansteigen.

LG

Woher ich das weiß: eigene Erfahrung – Ich habe Mathe gemacht.