Hallo
Ich habe eine Aufgabe zu Extremwertproblemen auf und komme da irgendwie nicht weiter bzw. auf ein falsches Ergebniss...
Die Aufgabe lautet: "Wie müssen die Maße eines zylindrischen Wasserspeichers ohne Deckel mit dem Volumen 1000l gewählt werden, damit der Blechvorrat minimal ist?"
Hab dann ganz normal Haupt- und Nebendbedingung aufgestellt.
Hauptbedingung:
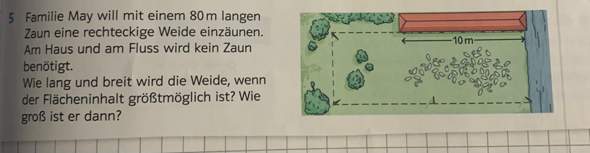
O = pir^2 + 2pirh (Bereits Deckel abgezogen)
Nebenbedingung:
1000l = pir^2h
Dann habe ich die Nebenedingung nach h aufgelöst um diese dann in die Hauptbedingung einzusetzen:
h = 1000l / pi*r^2
Durch einsetzen komme ich auf folgende Zielfunktion:
O(r) = pir^2 + 2pir(1000 / pi*r^2)
Habe noch die Klammer aufgelöst und gekürzt:
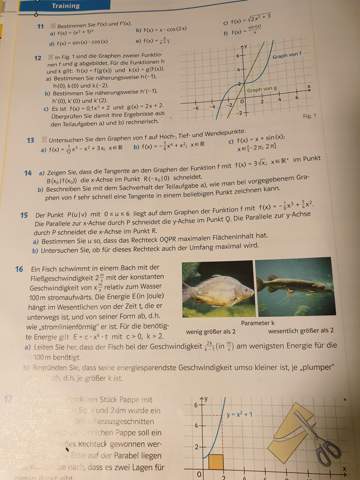
O(r) = pi*r^2 + 2000 / r
Dann abgeleitet um die notw. und hinr. Bedingung zu machen.
O'(r) = 2pir - 2000 / r^2
O''(r) = 2*pi + 2000/ r^3
notw.Bed.: O'(r) = 0
0 = 2pir - 2000 / r^2 | + 2000 / r^2
2000 / r^2 = 2pir | / r^2
2000 = 2pir^3 | / 2pi
2000 / 2pi = r^3 | 3te Wurzel ziehen
r = 6,83
Aus der hinr. Bed. ergibt sich ein Tiefpunkt, was auch gefordert ist.
Wenn ich alles in O(r) einsetze, um den Oberflächeninhalt herauszubekommen, erhalte ich als Ergebniss 911,859.
Mein Problem ist jetzt, wenn ich eine Probe mache, indem ich Die Hauptbedingung ebenfalls nach h umforme und alle Werte einsetze, diesen h Wer die Volumen Formel einsetze, komme ich nicht auf die 1000 Liter Volumen.
Daher glaube ich, dass ich einen Fehler gemacht habe.
Es wäre nett, wenn ihr mir sagen könntet wo dieser liegt :)
LG Philip