Wieso ist diese Polynomfunktion streng monoton steigend?
Hi, könnte mir jemand erklären warum diese Funktion streng monoton steigend ist? Bitte wenns geht auch erklären warum die anderen falsch sind, da mir ein paar unklar sind.
Dankeschön schon mal im Voraus!
4 Antworten
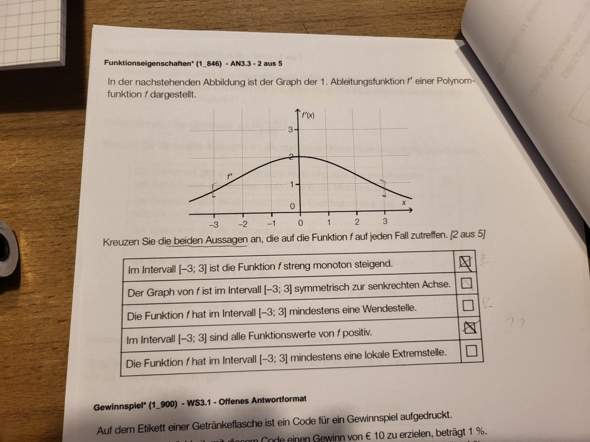
1) (richtig) Weil die Ableitung f' (=Steigung) im Intervall stets echt positiv (also größer als 0) ist. Würde der Graph von f' die x-Achse berühren, dann hätten wir es hier mit einem Sattelpunkt zu tun und es wäre nur noch "einfache" Monotonie (nicht streng). Würde der Graph von f' die x-Achse durchkreuzen, dann gäbe es gar keine Monotonie, denn die Steigung wird beim Durchtritt durch die x-Achse negativ.
2) (falsch) Wenn die Funktion streng monoton steigt, dann sie nicht spiegelsymmetrisch sein, wenn man auf halber Strecke die Spiegelachse anlegt.
3) (richtig) Die Funktion f hat bei x=0 die größte Steigung, während sie davor und danach abflacht. Genau das ist ein Wendepunkt.
4) (falsch) Wenn die Funktion f einen konstanten Term enthält (z.B. -10), dann fällt dieser bei der Ableitung weg. Die dargestellte Ableitung gibt also keine Auskunft über die genauen Funktionswerte.
5) (falsch) Lokale Extremstellen wären in der ersten Ableitung als Nullpunkte erkennbar. Die dargestellte Ableitung berührt die x-Achse im Intervall jedoch nicht.
dann hätten wir es hier mit einem Sattelpunkt zu tun und es wäre nur noch "einfache" Monotonie (nicht streng).
Auch eine Funktion mit Sattelpunkt kann streng monoton sein. Beispiel f(x) = x³
Ach f'(x)
.
Weil f'(x) immer positiv ist , trifft a) zu ( auch wenn die Steigung mal größer mal kleiner wird )
.
bei sym müssten die einen Steigungen pos , die anderen neg sein
.
Hier : blau ist f' von grün
grün ist f' von rot , einer sym fkt


Der Graph zeigt die Ableitung f'(x) der Funktion f(x) und da die Ableitung die Steigung einer Funktion ist, geht es auch bei f(x) immer "bergauf" wenn die Steigung größer als 0 ist.
Weil f‘>0 für alle x im Intervall