Hat die graue Funktion einen Wendepunkt oder einen Flachpunkt?
Hallo,
Aufgabe 2 bereitet mir Kopfschmerzen.
Hier eine mögliche Stammfunktion:
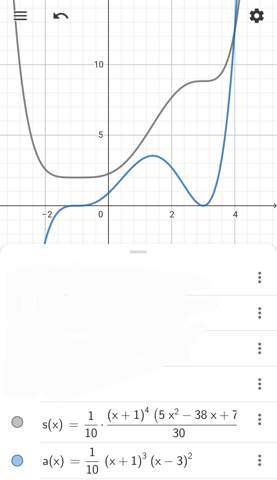
Dass der graue Graph einen Wendepunkt bei ca. x = 1.5 hat (weil die Ableitung da ein Extremum besitzt) leuchtet mir ein. Aber bei x=-1 hat die graue Funktion doch einen Flachpunkt und keinen Wendepunkt?! Die Krümmung wechselt ja auch nicht bei x=-1?!
Lösung
Was soll denn ein Flachpunkt sein?
Wenn an einer Stelle x0 gilt f''(x0) = 0. Im Gegensatz zum Wendepunkt muss bei ihm keine Änderung der Krümmung stattfinden.
Dann hätte f(x) = x³ bei x = 0 einen Flachpunkt. Das ist aber nicht so.
Tatsächlich schon. Bei x=0 hat x^3 einen Sattelpunkt. Ein Sattelpunkt ist ein Wendepunkt mit waagerechter Tangente, ein Spezialfall eines Wendepunktes.
Tatsächlich nicht, denn du sagst doch, dass sich bei einem
Flachpunkt das Krümmungsverhalten nicht ändert. Das tut
es aber bei x³, also ist es kein "Flachpunkt".
Wann habe ich das gesagt? Ich habe geschrieben:"muss bei ihm keine Änderung der Krümmung stattfinden.". ->KANN, MUSS aber NICHT zwangsläufig stattfinden. FLP->WP->SP
1 Antwort
Aber bei x=-1 hat grau doch einen Flachpunkt und keinen Wendepunkt?! Die Krümmung wechselt ja auch nicht bei x=-1?!
... und was ist dann Dein Problem mit dieser Tatsache? Im Aussage (2) steht ja etwas von "genau einen Wendepunkt" im Intervall [-1,2]
(Im Übrigen ist bei x = -1 ein lokales Minimum)
Da schließe ich mich an...du hast in diesem Intervall genau einen Wendepunkt, also alles richtig.
Was interessiert die Lösung, wenn sie falsch ist für Aussage (2). Und was soll das mit dem Flachpunkt? Bei x = -1 ist ein Minimum und das nennt man einen Tiefpunkt. Von einem Flachpunkt habe ich noch nie etwas gehört (Das ist für mich ein waagerechter Wendepunkt = Sattelpunkt).
Hast du die Aufgabe richtig gelesen? Der Graph zeigt lediglich die Ableitung. Ein Sattelpunkt ist eine spezielle Form des Wendepunkts mit waagerechter Tangente Beim Wendepunkt gilt f''(x0) = 0 und f'''(x0)≠0, damit ein Krümmungswechsel auftritt. Der Flachpunkt schließt den Wendepunkt mit ein, bei ihm gilt nur f''(x0) = 0. Da der Graph (Ableitung) an der Stelle x=-1 zwar die Bedingung f''(x0) = 0 erfüllt, aber nicht die 2. für den Wendepunkt, ist es ein Flachpunkt. Sieht man doch auch, weil die Krümmung (bei grau, der Stammfunktion) nicht wechselt.
Beim Wendepunkt gilt f''(x0) = 0 und f'''(x0)≠0, damit ein Krümmungswechsel auftritt.
Was ist dem nach mit f(x) = x^5? Bei 0 ist dort ja wohl eindeutig ein Krümmungswechsel?
Allgemein: Ist f'''(x) ungleich 0, so ist dort ein Wendepunkt, die Umkehrung gilt aber nicht.
Woher stammt der Begriff "Flachpunkt" In der Aufgabe sehe ich ihn nicht.
Die Hierarchie Flachpunkt -> Wendepunkt -> Sattelpunkt haben wir im Unterricht behandelt. Ich verstehe nur nicht, warum die Aussage 2 falsch ist. Ich dachte nur bei ca x=1.4 sei ein Wendepunkt. Ich verstehe nicht, wie bei x=-1 noch einer sein kann.
Weil links und rechts von dem Punkt die Krümmung wechselt. Wäre der Graph allgemein auf den angegebenen Bereich beschränkt, wäre dort keiner. f ist aber nicht im Definitionsbereich beschränkt sondern nur die Betrachtung bzgl. Wendepunkte. Wichtig ist noch, dass es ein abgeschlossenes Intervall ist.
Aber wo siehst du bei x=-1 (für f) einen Wendepunkt??? Ich sehe in der Abbildung(f'(x)) links von -1, dass die Steigung zunimmt, je dichter an -1 aber immer weniger zunimmt. Rechts von -1 immer mehr und mehr. Also ist bei (zwar unterschiedlich stark) aber durchgängiger Zunahme der Graph f dort durchgängig linksgekrümmt?! Wo ist der Krümmungswechsel? Die Abbildung zeigt ja nur die Ableitung, nicht die ursprüngliche Funktion.
Du hast recht, dass es die Ableitung ist, habe ich übersehen. Wendepunkte sind Punkte extremer Steigung. die Abbildung zeigt in dem Bereich nur ein Extremum. Damit verstehe ich die "Lösung" auch nicht...
Haha, ist mir in der letzten Klausur auch schon passiert... ;)
Ok, also du würdest sagen, dass es in dem Interval nur einen Wendepunkt gibt?! Ich stelle mal die Lösung mit ein, aber ich habe das Gefühl, dass die Autoren sich da 10 mal verschrieben haben.
Was ist denn nun deiner Meinung nach x=-1 für eine Stelle beim Graph von f(x)?! :)
In der Lösung ist der Wurm drin: An der Stelle 1 hat f sicher keine doppelte Nullstelle. Das wäre ja zwingend ein Extremum und damit Nullstelle in f'. Auch die weiteren "Begründungen" kann ich nicht nachvollziehen. Bei -1 hat f' (also der abgebildete Graph) eine Nullstelle mit Vorzeichenwechsel und damit f eindeutig ein Extremum und keine Wendestelle.
Wie genau lauten die Bedingungen für einen Flachpunkt ? Ein FP ist kein Extremum ? ( HP oder TP )
Ja, aber in den Lösungen steht die Aussage sei falsch. Ein Flachpunkt ist ja kein Wendepunkt.