Wendepunkt E funktion?

f(x)= x*e^(-x^2)

ich weiß Dass die funktion keinen WP hat aber wie sieht es aus wenn man die 2. Ableitung gleich Null setzt also welchen Ansatz hat man da und wo erkennt man dann ANHAND DER RECHNUNG dass es keinen Wendepunkt gibt.

Answer 1

[evtldocha]

ich weiß Dass die funktion keinen WP hat

Seltsam: $f''\left(x\right)=(4x^3−6x)\cdot e^{−x^2}\ =\ x\cdot\left(4x^2-6\right)\cdot e^{-x^2}$

Da bleibt es dann nicht nur bei einem Wendepunkt.

Answer 2

[Willy1729]

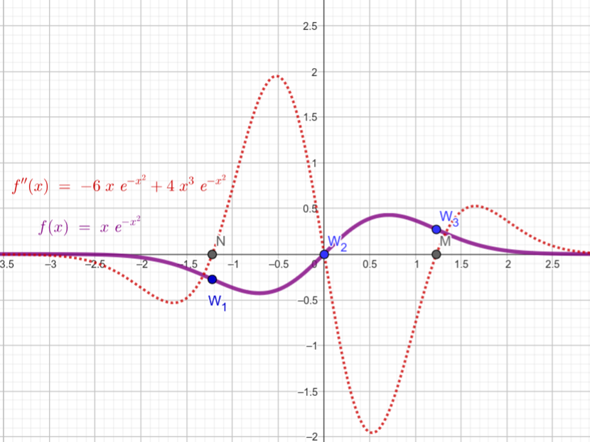
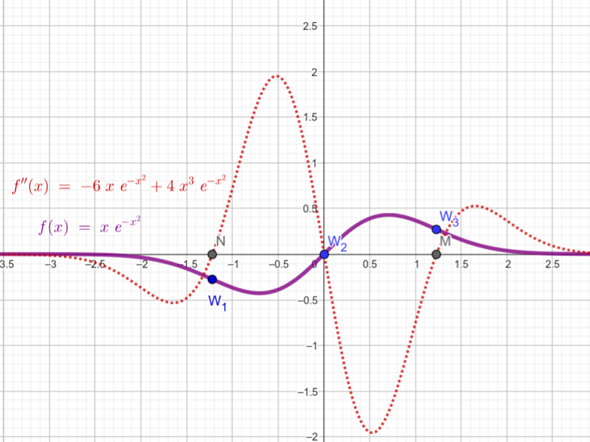
Hallo,

die Funktion hat sogar drei Wendepunkte, nämlich bei x=0 und bei x=±Wurzel (3/2).

Zweimal ableiten, zweite Ableitung gleich Null setzen, lösen.

Herzliche Grüße,

Willy

Comments

[rumar]

"Zweimal ableiten, zweite Ableitung gleich Null setzen, lösen."

Wenn f"(x) = 0 ist, garantiert dies allein noch nicht die Existenz eines Wendepunktes an der Stelle x . Eine Überprüfung (z.B. mittels der dritten Ableitung f'''(x) ist erforderlich.

Answer 3

[Halbrecht]

ich weiß Dass die funktion keinen WP 

dein Wissen ist falsch . Übe weiter ableiten . Denn nur da kann dein Fehler liegen

.

Hier wirklich kein WP 

f(x) = e^(x²) 

f'(x) = 2x * e^(x²) 

f''(x) = (2+4x²) * e^(x²) 

0 = (2+4x²)

-2/4 = x²

hat keine Lösung , also auch kein WP 

So erkennt man das