Bedeutung der dritten Ableitung?
Hallo liebe Matheprofis,
wie auch bei meiner letzten Frage, habe ich erneut ein Verständnisproblem- diesmal aber bei der dritten Ableitung im Bezug auf Wendepunkte.
Um zu überprüfen, ob ein Wendepunkt vorliegt, muss die 2. Ableitung an diesem Punkt 0 sein. Als hinreichendes Kriterium muss außerdem ein Vorzeichenwechsel beim Graph der 2. Ableitung vorliegen.
Dieses hinreichende Kriterium kann auch die dritte Ableitung übernehmen (wenn f‘‘‘(x)>0 = Rechtskurve zu Linksurve und wenn f‘‘‘(0)<0 = Links zu Rechtskurve). Nur leider verstehe ich diesen Zusammenhang nicht wirklich.
Meine Vermutung wäre, dass die Steigung der zweiten Ableitung bei f‘‘(x)=0 positiv sein muss, damit der Graph der zweiten Ableitung an dieser Stelle vom negativen, zum positiven übergehen kann. (Genau andersherum beim negativen). Leider finde ich dazu aber überhaupt keine Erklärung im Netz.
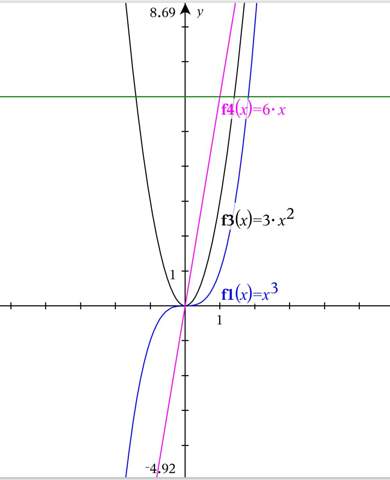
Vielleicht kann mir jemand den Zusammenhang anhand dieses Beispiels erklären (f(x)=x^3)
Hat vielleicht jemand von euch eine anschauliche Erklärung?
Liebe Grüße
2 Antworten
bezogen auf f(x) = x³ wäre die Graphen so richtig
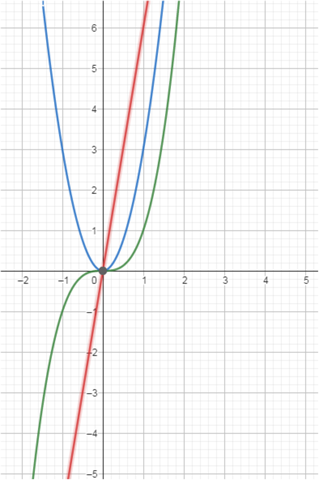
6x ist eine Gerade .
von links aus bis 0 ist sie im Minusbereich . Dort ist f(x) eine Rechtkurve . Ab 0 positiv , also Linkskurve
bei x = 0 ist f''(x) = 0 . Dort geht die Rechts in die Linkskurve über , was ein Wendpunkt ist ( f(x) ändert die Krümmungsrichtung )
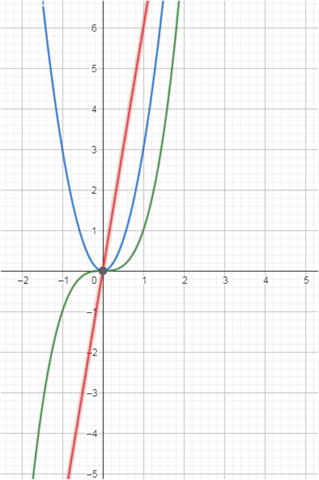
Danke! Eigentlich habe ich mich nur gefragt, wieso die dritte Ableitung genauso Auskunft über das Wendeverhalten geben kann. (Sie löst ja das Vorzeichen-Wechsel Kriterium ab)
Ich habe leider gerade nicht die möglichkeit das grafisch darzustellen, aber wenn du zugriff auf irgendein Programm hast, welches Funktionen Grafisch darstellen kann (ein grafischer Taschenrechner zum Beispiel), dann mach das und vielleicht hilft dir das bereits