Wieso gibt es hier keine Lösung?
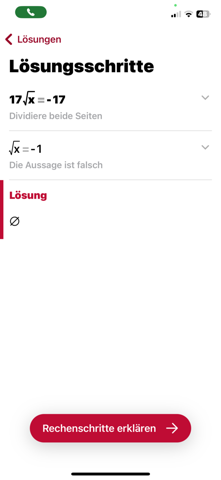
Im letzten Schritt doch einfach ^2 machen und dann ist es x = 1?
4 Antworten
Das Quadrieren ist keine eineindeutige Rechenoperation (Äquivalenzumformung).
Beispiel: Wenn ich annehme, dass - 1 = 1 ist dann würde aus dieser falschen Aussage durch Quadrieren die wahre Aussage 1 = 1 folgen.
Dadurch wird aber die falsche Aussage - 1 = 1 nicht zu einer wahren Aussage.
Quadrieren ist keine Äquivalenzumformung!
Beispiel:
-3 = 3 ist offensichtlich falsch.
Quadriert man diese Gleichung allerdings
(-3)²=3²
9=9
haben wir einen Widerspruch.
Deine Gleichung hat also in der Menge der reellen Zahlen R keine Lösung, erst durch Erweiterung auf die Menge der komplexen Zahlen C ergibt sich die Lösung
i²=-1
Aber keine Angst, das kommt erst in der Sekundarstufe II in Mathe.
Weil die Wurzel einer beliebigen Zahl nie negativ ist
Schon der 1. Term ist falsch.
Die Wurzel einer Zahl mit einer positiven weiteren Zahl multipliziert kann nie negativ sein.
Der Term ist nicht falsch, er hat nur keine Lösung in R.
Algebra in der Schulmathematik kann man eigentlich auf einen Satz reduzieren: "Das können wir mit der jetzt bekannten Zahlenmenge nicht lösen, und darum erweitern wir diese Zahlenmenge"