Wie fasst man 4^x - 4^x zusammen?
Und ist es richtig, wie ich es grob ausgerechnet habe?
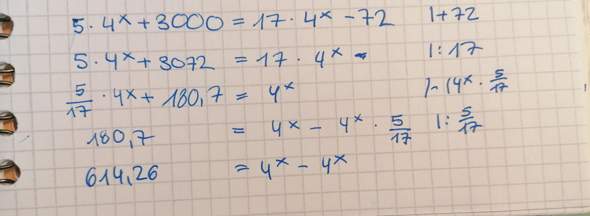
5 Antworten
4^x - 4^x ist gleich 0. Denn allgemein ist a - a = 0 für jeden Wert a.
============
ABER: Du hast dich vorher verrechnet. Wenn man
durch 5/17 teilt, so erhält man nicht
Man kann ja nicht einfach nur hinten das 4^x * 5/17 hinter dem Minus durch 5/17 teilen, sondern muss natürlich auch das vordere 4^x vor dem Minus durch 5/17 teilen und würde dann nämlich stattdessen
erhalten.
============
Was man machen könnte (statt so falsch durch 5/17 zu teilen), wäre
zu vereinfachen und dann durch 12/17 zu teilen (bzw. mit 17/12 zu multiplizieren).
====== Ergänzung ======
Lösungsvorschlag zum Vergleich...
1 ist das neutrale Element der Multiplikation. Dementsprechend kann man, wenn benötigt, einfach ein „ ⋅ 1“ ergänzen, ohne den Wert zu verändern.
Also...
4^x - 4^x ⋅ 5/17
= 4^x ⋅ 1 - 4^x ⋅ 5/17
= 4^x ⋅ (1 - 5/17)
Bzw. etwas allgemeiner...
a - a ⋅ b = a ⋅ 1 - a ⋅ b = a ⋅ (1 - b)
Nein, das ist falsch, denn 3072/17 kann niemals eine Kommazahl mit nur einer Stelle sein.
Ja natürlich, hab ja nur aufgerundet. Wollte jetzt nicht die 10 anderen Nachkommastellen dazu schreiben.
Ab der dritten Zeile wird es falsch.
Rechne auf beiden Seiten der Gleichung: -5 * 4^x
Dann hast Du: 3072 = 12 * 4^x
...
Hallo,
wenn Du etwas von sich selbst abziehst, bleibt Null übrig.
Ob dieses Etwas 4^x oder Susanne heißt, ist dabei egal.
Herzliche Grüße,
Willy
Daß es zu 4^x-4^x nur durch einen Fehler gekommen ist, sollte Dir inzwischen klar sein. x ist übrigens gleich 4.
Du hast bei Deiner Rechnung beim Übergang von der vorletzten zur letzten Zeile einen Fehler gemacht - hier hätte 4^x ausgeklammert werden müssen…
Hey, vielen Dank für die ausführliche Erklärung! Könntest du mir nur noch sagen, wie du auf die 1 gekommen bist bei 4^x (1-5/17)?