Extrem und Wendepunkt?
Hey
habe hier einen Graphen den ich auf Monotonie untersuchen soll. Also habe die erste Ableitung von ihm und verwirrt mich ein bisschen. Siehe Bild. Ist also bei g an der Stelle x=2 ein Extrempunkt oder ein Wendepunkt oder irgendwie beides? Danke schonmal für eine schnelle Antwort.
Ciao

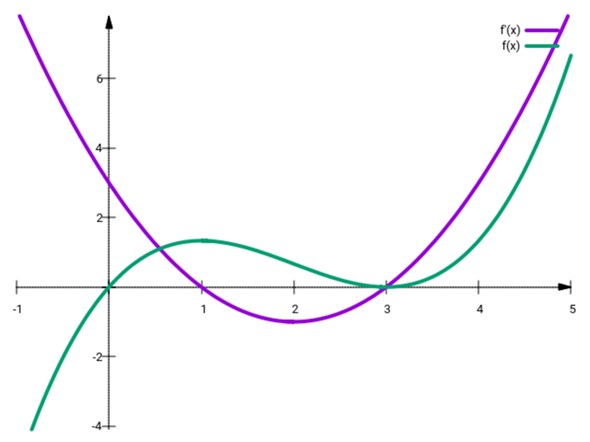
Im Graphen sind die beiden Funkionen mit f’ und g’ bezeichnet. Sollst Du etwas über die Monotonie der abgebildeten Funktionen (f’, g’) oder der Stammfunktionen (f, g) aussagen?
Ich soll zu f und g aussagen
4 Antworten
Bei 2 hat g einen Sattelpunkt (Wendepunkt mit waagerechter Tangente).
st also bei g an der Stelle x=2 ein Extrempunkt oder ein Wendepunkt oder irgendwie beides? Danke schonmal für eine schnelle Antwort.
Es ist nicht eine "normale" Nullstelle , sondern ein Berührpunkt ( dh y = 0 )
so könnte g(x) aussehen , wenn g'(x) so aussieht wie bei dir

bei x = 4 ein "echter" HP , bei x = 2 ein Wendepunkt mit waagrechter Tangente ( nennt man Sattelpunkt )

Die erste Kurve (blau) ist f’(x). Sie ist positiv außerhalb des Intervalls 1≤x≤3, also steigt die Funktion f(x) dort an; in diesem Intervall ist sie negativ, also fällt f(x) im Bereich zwischen 1 und 3. An den Punkten 1 und 3 gibt es Extrema in f(x), und dort wo f’(x) ein Extremum hat (bei x=2), hat f(x) einen Wendepunkt.

Als zweites haben wir die rote Kurve g’(x). Die ist nichtnegativ für x≤4, also muß g(x) in diesem Bereich steigen; wegen der Nullstelle f’(2)=0 hat g(x) dort eine horizontale Tangente. Für x≥4 hat g’(x) negative Werte, also muß g(x) dort fallen.

Auch hier siehst Du, daß g(x) einen Wendepunkt hat, wenn g’(x) ein Extremum hat (an den Punkten x=2 und x=3½)
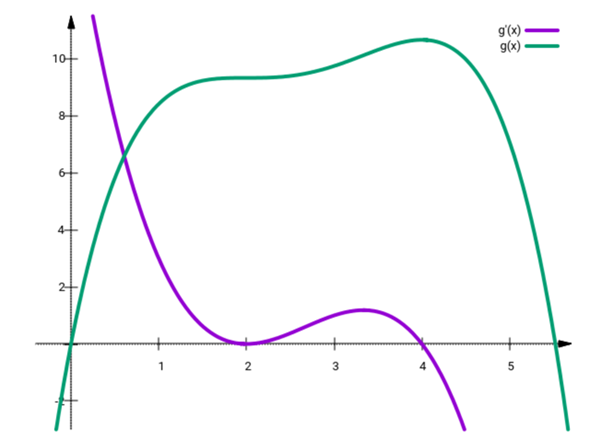
Bei g ist ausschließlich ein Wendepunkt. Ein Extrempunkt ist hier nicht, denn die Ableitung wechselt nicht das Vorzeichen.