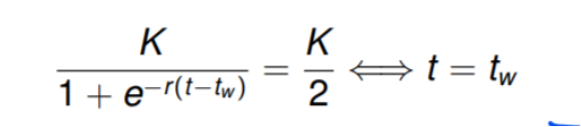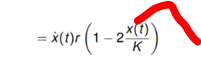Logistisches Wachstum Wendepunkt finden?

Es geht um die Lösung x(t), die von unten nach K strebt und einen Wendepunkt tw hat. Hier sind die Formel für Lösung und tw.

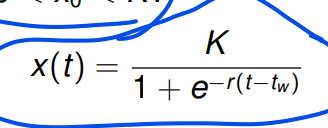
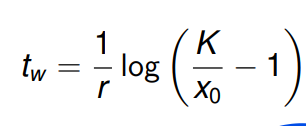
Jetzt will man die Wendepunktformel herleiten. Und zwar müsste man eine Stelle finden, wo es keine Änderung der Änderungsrate von x(t) gibt, also wo x(t) sich weder beugt noch exponentiell steigt, und das ist am Wendepunkt. Deswegen hat man die Ableitung der Änderungsrate gebildet und sucht eine Stelle, wo sie 0 ist. Das hat man auch gefunden, nämlich K/2.

Meine Frage ist jetzt, wie kommt man jetzt auf die Formel für tw? Von der ganz unteren Gleichung kannn ich nur folgern, wenn t=tw, wird der e-Teil 1, und der Nenner 2, weshalb die Gleichung stimmt. Aber wie kommt man auf die obere Formel? Ich dachte, das wäre eine Art Herleitung?

Answer 1

[Halbrecht]

alles recht schwer verständlich für . Auf die Gefahr einer Wiederholung hin

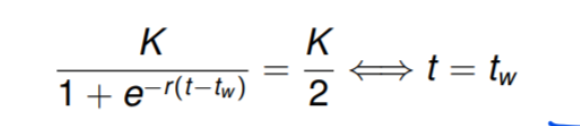
wenn t = tw , dann steht da K/(1 + e^(-r * 0 ) ) = K/(1+1)

.

Das soll die zweite

Ableitung sein . Durch denken stellt man fest , dass die Klammer NULL wird , wenn x(t) = K/2

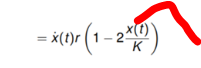
Aha , und nun fragt man sich , wann x(t) = K/2 wird und kommt zur Schlußfolgerung : wenn t = tw