Bruchgleichungen Hauptnenner?
Wann und warum muss ich dieses komplizierte Verfahren machen, wenn ich doch einfach |*(6-3x)*(2x-4) machen könnte oder?

4 Antworten
Du kannst tatsächlich beide Rechenwege wählen. Aber in dem in der Beschreibung verwendeten Verfahren geht es darum den kleinstmöglichen Hauptnenner zu finden. Dazu ist es eben empfehlenswert die beiden Nenner zunächst durch ausklammern und umformen soweit wie möglich zu vereinfachen. Der Vorteil ist (bei diesem Beispiel) am Ende, dass nur mit einem Klammerterm und nicht mit zweien multipliziert werden muß, du ersparst dir damit am Ende ein Ausmultiplizieren.
Weiter ist es empfehlenswert sich an das vorgegebene Verfahren zu halten, da sonst Punktabzüge drohen.
Ich finde das jedoch blöd, wenn Lehrer sich auf ein Verfahren versteifen. Das nimmt den Schülern oft die ach so wunderschöne mathematische Kreativität.
wenn ich doch einfach |*(6-3x)*(2x-4) machen könnte oder?
ja . So kann man immer vorgehen. Was hier zu Zählern führt , die noch übersichtlich sind. Sollten es aber mehr als 2 Brüche sein oder komplizierte , empfiehlt es sich das Verfahren der Ausklammerung zu testen . Muss ja auch nicht immer funktionieren .
Was du als "kompliziertes Verfahren" bezeichnest ( das Ausklammern ) , ist ein Standardverfahren , was man beherrschen sollte .
.
Zwar bringt 36x³ = 9x² * 4x hier nicht wirklich viel ( was an meinem Beispiel liegt ) , trotzdem wäre der Hauptnenner nach Holzhammermethode schon ein übler , oder ?
nämlich der
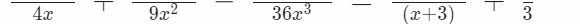
wenn man das Produkt bildet .
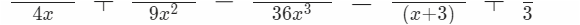
Das Verfahren macht vor allem dann Sinn, wenn im Nenner und im Zähler kompliziertere Terme stehen. Durch das Ausklammern kann dann häufig eine starke Vereinfachung erzielt werden. Im Extremfall würde man auf Gleichungen höheren als 2. Grades (oder sogar 5. Grades)) kommen, die von Schülern i. A. nicht gelöst werden können. Um das Verfahren zu lernen wird mit sehr einfachen Beispielen begonnen, die sich deshalb auch manchmal noch einfacher lösen lassen.
Das kannst du machen, du erhältst:
x*(2x-4)=3*(6-3x)
2x²-4x=18-9x
2x²+5x-18=0
x²+2.5x-9=0
x1/2=-1.25±√(1.25²+9)
x1/2=-1.25±√(10.5625)
x1/2=-1.25±3.25
x1=-4.5, x2=2
Du musst jetzt aber aufpassen, denn mit x2=2 hast du eine Scheinlösung erzeugt, die, wenn du einsetzt, 2 Brüche mit einer Division durch 0 erzeugt. Das passiert im anderen Verfahren nicht. 2 wurde aber aus dem Definitionsbereich ausgeschlossen.