Berechnen der Schnittpunkte (Polynomfunktion und lineare F.)?
Ich soll die Schnittpunkte der folgenden Funktionen berechnen:
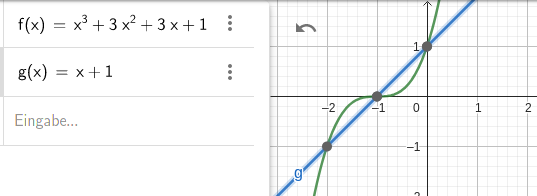
y = x^3 + 3x^2 + 3x + 1
y = x + 1
Lösungen sollen sein:
S1 (0|1) , S2 (-1|0) , S3 (-2|-1)
Die ersten 2 sind vertsändlich und kommen bei mir auch raus. Aber auf S3 komme ich nicht… Was mache ich falsch bzw. was übersehe ich?
Mein Rechenweg (siehe Bild):

Bitte um Hilfe! Danke.
Die Funktionsgleichung der PF lautet
y = x^3 + 3x^2 + 3x + 1
Habe die 3x in der Fragestellung vergessen!
4 Antworten
du willst die Schnittpunkte von x+1 und x³+3x² + 3x + 1 rausfinden ?
.
Wenn du einen davon mit y = x+1 bestimmen will , gehst du davon aus , dass die Nullstelle der lineFkt auch Schnittpunkt ist .
Das ist hier so , aber das ist ZUFALL !
.
eine PolyDiv ist hier nicht nötig nachdem man
x+1 = x³+3x² + 3x + 1
gebildet hat . Die übliche Art Schnittpunkte zu finden
Eine PolyDiv ist sogar FALSCH , weil du mit ihr nur Nullstellen findest von f(x) , nicht die gesuchten Schnittpunkte. Brauchst du nicht !
.
Wenn man NACH dem Gleichsetzen immer noch eine kubische Glg hat , wo man kein x ausklammern kann , dann ja dann ist eine PolyDiv nötig
Super verständlich und hilfreich! Gut, dass es euch gibt ~ Danke!
x³ + 3x² + 3x + 1 = x + 1
x³ + 3x² + 2x = 0
x(x² + 3x + 2) = 0
x_1 = 0
x² + 3x + 2 = 0
x = -1,5 +-√(1,5² - 2)
x_2 = -2
x_3 = -1
Deine Rechnung verstehe ich nicht: Aus
folgt:
Und damit:
Damit ist die erste Nullstelle x=0. Für die Klammer nimmst Du die pq-Formel

Nein! Du rechnest nicht Nullstellen eines der beiden Polynome aus, sondern Nullstellen der Differenz der beiden Polynome. Die Graphen schneiden sich, wenn die Differenz Null ist
ich habe in meiner Rechnung eine Polynomdivison durchgeführt.. Dadurch sollte man ja auch auf die Nullstellen kommen..?
Das habe ich gesehen. Aber was soll eine Polynomdivision hier? Eine Polynomdivision macht man wenn man eine Nullstelle des Polynoms, für das man alle Nullstellen sucht, bereits kennt. Du hast aber schon das Polynom, für das Du die Nullstellen benötigst, nicht korrekt. Du benötigst doch die Nullstellen von
Hiervon kannst Du eine Nullstelle raten und dann eine (unnötige) Polynomdivision machen.
Ich soll die Schnittpunkte der folgenden Funktionen berechnen:
y = x^3 + 3x^2 + 1
y = x + 1
x^3 + 3x^2 + 1 = x + 1
x³ + 3x² -X = 0
X * (x²+3x-1)=0
Jetzt Satz des Nullproduktes. Du hattest was falsches vor dem x
Toll, Danke! Bin auf die Lösung jetzt durch dich gekommen.
Sollte man aber nicht auch auf die richtige Lösungsmengen durch eine Polynomdivision kommen?
Schnittstellen von Polynom-Funktionen berechnet man nicht durch Division der Polynome sondern durch Gleichsetzen der Polynome.
Hmmm… Und gibt‘s einen Weg um auf den Schnittpunkt mit der Y Achse der Polynomfunktion zu kommen? Also auf (0|1) anhand der gegebenen Polynomfunktion?
Außer, dass man d von der Linearen abliest.
Der Schnittpunkt mit der y-Achse interessiert doch prinzipiell hier nicht. Es ist nur insofern hier offensichtlich, dass der bei y=1 ist, weil die beiden Polynome so einfach sind. Aber auch dann bleibt es dabei, dass Du
x³ + 3x² + 2x : x - 0
rechnen müsstest um dann die zweite und dritte Nullstelle zu bekommen.
dummer Zufall hier : dass die Nullstelle von (x+1) auch Schnittpunkt beider Fkt ist .
Diese Aufgaben hasse ich . Da erwarte ich vom Aufgabenerstellerin etwas Mitdenken .
Ja - blöd, aber es wäre prinzipiell "Vorwissen", wenn ich meinen Lösungsweg danach wählen würde.
Wenn die erste Nullstelle 0 ist müsste der Graph dann nicht durch (0|0)?