Abstand zweier paralleler Geraden?
Gegeben sind die Geraden f(x)=3x-8 und g(x)=3x+2.
a) Begründen Sie, dass f und g parallel zueinander sind.
b) Berechnen Sie den Abstand der beiden Geraden.
Freue mich auf Lösungen mit Rechenweg. Danke!
2 Antworten
Bitte schau mal nach, wie der Abstand zweier Geraden
definiert ist.
Und hier eine Abbildung, die zeigt, dass der Abstand nicht 10 LE beträgt, sondern nur Wurzel(10). Kann berechnet werden mit der senkrechten Geraden deren Steigung -1/3 beträgt. Siehe Bild:
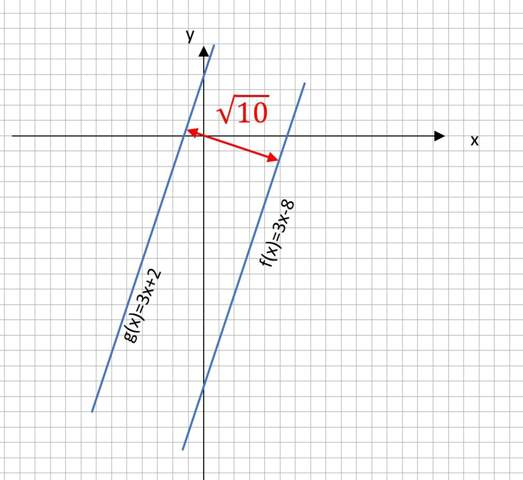
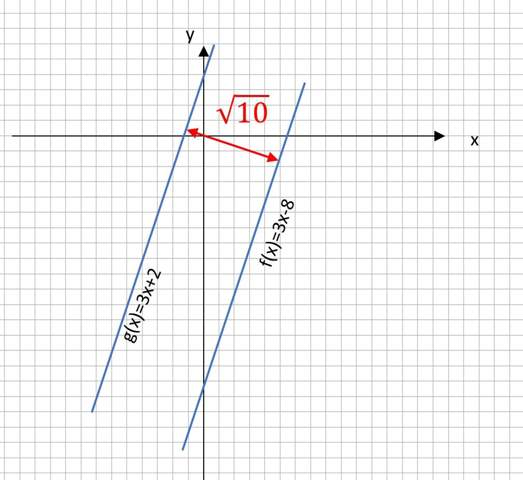
A) Die Steigung m ist gleich.
B) |f(1)|+|g(1)|=5+5=10
kb hätte es so gemacht in 12 jahren schule noch nie gebraucht oder gesehen
Das ist nicht der Abstand der beiden Geraden, sondern nur der Abstand zwischen ihren Schnittpunkten mit der y-Achse.
Der Abstand ist Wurzel (10), läßt sich u.a. über Winkelfunktionen berechnen.
Du hast die y-Werte verglichen. Das ist nur bei Geraden der Abstand, die parallel zur x.Achse verlaufen.
Bitte schau mal nach, wie der Abstand zweier Geraden
definiert ist.