Wahrscheinlichkeitsrechnung, habe die Lösungen, verstehe nur nicht, wie man darauf kommt?
Aufgabe lautet:

Betrachten wir mal nur die Prozessoren, ein Prozessor kann mit einer Wahrscheinlichkeit von 0,5%(=0,005) ausfallen, ich habe zwei Prozessoren, mit welcher Wahrscheinlichkeit kann ich davon ausgehen, dass beide Prozessoren den Geist aufgeben? Das Ergebnis ist ja 0,005^2, aber warum? Also warum sagt man, dass man das quadriert?
Lösung:

Warum darf ich jetzt einfach bei der Wahrscheinlichkeit, dass keine Einheit ausfällt, die Wahrscheinlichkeiten multiplizieren? Da steht, da die unabhängig sind, aber warum darf man deshalb das multiplizieren?
Mein größtes Problem ist, warum ich am Ende die Wahrscheinlichkeiten multipliziere? Das mit dem quadrieren habe ich jetzt kapiert, aber warum multipliziere ich das?
3 Antworten
Antwort wurde bearbeitet.
Wenn die Ereigniesse stochastisch abhängig wären, dann würde das Ergebnis verfälscht werden. Falls ihr schon die Einführung in die bedingte Wahrscheinlichkeit hattet, hilft dir sicher dieses Video.
Man muss die Wahrscheinlichkeiten multiplizieren, da es keine andere Möglichkeit gäbe, die "Gesmamtwahrscheinlichkeit" im Intervall [0,1] zu behalten - klingt erstmal wirrkürlich, ist es evtl. auch, denn es kommt darauf an, wie man die Wahrscheinlichkeit interpretiert.
Wenn zwei Ereignisse eine Wahrscheinlichkeit Wahrscheinlichkeit zugeordnet wird, dann ist die Hintereinanderausführung das Produkt dieser Wahrscheinlichkeiten, da es nur Sinn macht, dass die Wahrscheinlichkeit geringer wird. Dies geht nunmal nur mit der Multiplikation mit der Zielmenge des Intervalls [0,1].
Es gibt da sicher deutlich bessere Erklärungen als meine, aber eines kann ich Dir sagen:
Die Mathematik beschäftigt sich nicht mit der Frage, was Wahrscheinlichkeit eigentlich ist bzw. wie man sie zu interpretieren hat. Die Mathematik definiert die Wahrscheinlichkeit einfach als eine Funktion für die eben unter anderem folgendes gilt:
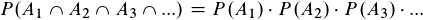
Ich hoffe, dass ich es einiger Maßen gut erklären konnte :)
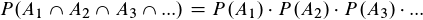
Naja ich denke dein Fehler liegt darin, dass du nicht alle Möglichkeiten berücksichtigst. Du musst ja auch Varianten beinhalten, wo alle Prozessoren gehen, 2 Netzteile ausfallen und die Festplatte nicht geht. Du musst jeden Weg nehmen, wo wirklich nur ein System ganz ausfällt, der Rest kann jeden Zustand annehmen. Dabei entstehen unzählige Möglichkeiten.
Aber das habe ich doch berücksichtigt.
Und das Ergebnis aus der Lösung macht doch auch gar keinen Sinn:
Alleine die Wahrscheinlichkeit, dass die Festplatte ausfällt, liegt schon bei 1%. Somit kann das Endresultat doch niemals bei rund 1% liegen... schließlich gilt für die anderen eine Wahrscheinlickeit kleiner als 1% (wenn man alle Komponenten berücksichtigt).
Zu deiner Frage. Wenn ein Ereignis die Chance x hat, beim einmaligen Versuch einzutreten, dann hat das Ereignis bei n-Versuchen die Wahrscheinlichkeit x^n. Du multiplizierst die Wahrscheinlichkeiten dafür, dass kein System vollständig ausfällt, weil es das Gegenereignis davon ist, dass ein System gleichzeitig ausfällt. Die Wahrscheinlichkeit, dass dss Ereignis A und B (hintereinander, oder gleichzeitig) auftreten berechnet man mit P(A)*P(B). Hier berechnet man also die Wahrscheinlichkeit, dass kein System ausfällt, und subtrahiert es von 1, um den Wert des Gegenereignisses zu bekommen.
Das ist mit "Unimathematik" getaggt. Das ist aber eigentlich Wissen, das man in Mathe im GK und im LK auf jeden Fall etwa ein Halbjahr lang behandelt hat (und normalerweise wird das Thema auch schon in der Mittelstufe zumindest angeschnitten).
Wenn die Eintrittswahrscheinlichkeiten für zwei Ereignisse P und Q jeweils p und q sind, dann ist die W., dass beide Ereignisse eintreten p * q.
Alles vergessen? Wegen Corona?
Mein größtes Problem ist, warum ich am Ende die Wahrscheinlichkeiten multipliziere?
Stell dir zwei Ereignisse vor, die nacheinander aber unabhängig voneinander auftreten, P(A)=0,1 P(B)=0,2
Von 1000 Leuten erleben 1000 * 0,1=100 das Ereignis A und 900 nicht (im Schnitt). Von den 100 erleben 100 * 0.2 = 20 auch das Ereignis B. D.h. die W., dass A und B beide eintreten, ist 20/1000 = 0,02 = 0,1 * 0,2
Bei deinem Prozessorenbeispiel werden die beiden Ausfallwahrscheinlichkeiten miteinander mal genommen. Da die für beide gleich sind rechnet man 0,005 * 0.005 = 0.005² =0,000025
Wenn das System läuft, wenn nicht beide Prozessoren ausfallen, dann benutzt man für die Durchhaltewahrscheinlichkeit das Gegenereignis. Die ist also
1 - 0,000025 = 0,999975 = 99,9975 %
Das kann man nicht alles hier erklären
https://studyflix.de/mathematik-schueler/thema/stochastik-153
Hilft
Danke, aber es ist doch so, wenn ich Wahrscheinlichkeiten mit UND verknüpfen will, multipliziere ich die und wenn ich sage ODER addiere ich die.
Wenn ich z. B. sage, eine Ente stirbt mit 5% Wahrscheinlichkeit und ich habe zwei Enten(Ente A und Ente B), mit welcher Wahrscheinlichkeit sterben beide?
Dann mache ich ja 0,5%(A)*0,5%(B)
wenn ich Sage mit welcher Wahrscheinlichkeit stirbt A oder B, dann mach eich doch 0,5%+0,5%, ist das so nicht korrekt?
Jetzt sage ich oben, dass das System zusammenfällt wenn einer der Komponenten kaputt geht
Dann müsste ich doch sagen Prozessor ODER Festplatte ODER Netzteil
Wenn ich z. B. sage, eine Ente stirbt mit 5% Wahrscheinlichkeit und ich habe zwei Enten(Ente A und Ente B), mit welcher Wahrscheinlichkeit sterben beide?
Und wenn eine mit 60% und die andere mit 70% stirbt? Dann überlebt mit 58% Wahrscheinlichkeit mindestens eine (also A oder B oder beide). Die Gegenwahrschwinlichkeit, dass beide sterben.
wenn ich Sage mit welcher Wahrscheinlichkeit stirbt A oder B, dann mach eich doch 0,5%+0,5%, ist das so nicht korrekt?
A oder B oder beide ist das Gegenereignis zu "beide überleben"
1 - 0,95² = 1 - 0,9025 = 9,75%
Nicht 10% !
(Ich hab jetzt versehentlich mit 5% gerechnet, aber das ändert nichts an der Vorgehensweise.)
Wir haben in der Uni 4 Semester nur Beweise gemacht in Mathe, also 2 Jahre keine Wahrscheinlichkeitsrechnung, jetzt kommt das wieder als basic diese Aufgabe und man hat alles halt vergessen
zu "Deinem" Supergau: ist doch korrekt. Dies ist die Wahrscheinlichkeit, dass alle 8 Komponenten ausfallen. Das ist nunmal bei diesen geringen Ausfallwahrscheinlichkeiten äußerst unwahrscheinlich...
Hier reicht ja schon aus, wenn nur eine Komponente komplett ausfällt, um das System lahm zu legen.