Wie kann ich den Scheitelpunkt berechnen?

Die Aufgabe lautet

y=x² +6x + 15

Wie mache ich das jetzt?

Answer 1

[ethan227]

Hallo,

Der Ziel dafür ist es, dass Du die Funktion y = x^2 + 6x + 15 in die Form y = ( a - m ) + n umwandeln solltest. In diesem Fall musst Du die quadratische Ergänzung nutzen, um die Gleichung in dieser Form zu bringen :

$x^2\ +\ 6x\ +\ 15\ =\ x^{2\ }+\ 6x\ +\ 9\ -\ 9\ +\ 15\ =\ \left(\ x\ +\ 3\right)^2\ +\ 6\$ Der Scheitelpunkt dieser Gleichung lautet dann : S ( -3 / 6 ). 😊

Oder Du kannst die erste Ableitung dieser Funktion finden, welche Du zu 0 einsetzen musst. Danach setzt Du den Wert von x auf der ersten Ableitung in die, originelle Gleichung ein.

y = x^2 + 6x + 15, y' = 2x + 6 = 0, x = -3

( -3 )^2 + 6(-3) + 15 = 9 - 18 + 15, ie. -9 + 15 = y = 6

Alles Gute für Dich. 🍀

Woher ich das weiß: Studium / Ausbildung – Mathematik ist seit langem mein Lieblingsfach.🧮

Answer 2

[evtldocha]

Wie mache ich das jetzt ?

Mit der quadratischen Ergänzung bringst Du die Gleichung in die Scheitelpunktform: $x^2+6x+15\ =\ x^2+6x+\left(\frac{6}{2}\right)^2-\left(\frac{6}{2}\right)^2\ +15\ =\left(x+3\right)^2+6$

Und nun kannst Du den Scheitelpunkt zu S(-3|6) ablesen.

Skizze:

Answer 3

[mihisu]

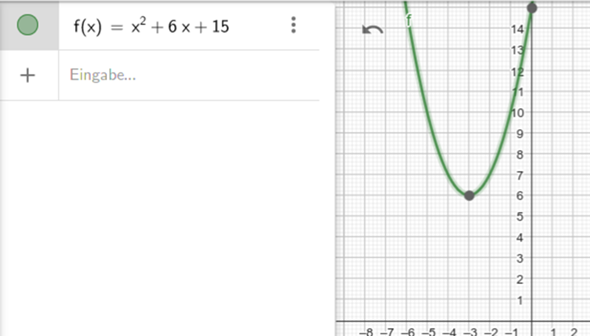
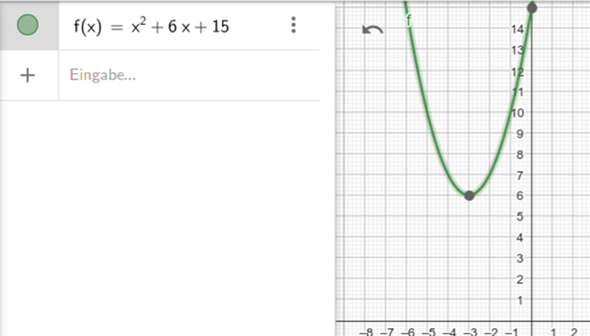
Da gibt es ein Verfahren, welches sich quadratische Ergänzung nennt.

https://de.wikipedia.org/wiki/Quadratische_Ergänzung

============

Im konkreten Fall musst du schauen, wie du x² + 6x zu einem Binom ergänzen kannst. Dazu brauchst du noch die Hälfte des Koeffizienten vor dem x, also die Hälfte von 6, also 3. Und diese 3 musst du quadriert addieren. Denn...

$x^2+6x+\left(\frac{6}{2}\right)^2=x^2+2\cdot x\cdot \frac{6}{2}+\left(\frac{6}{2}\right)^2=\left(x+\frac{6}{2}\right)^2$

bzw.

$x^2+6x+9=\left(x+3\right)^2$

Allerdings kann man da nicht einfach so 3² addieren, ohne den Wert zu ändern. Deshalb muss man zum Ausgleich wieder 3² subtrahieren.

=============

Das sieht dann so aus...

$y=x^2+6x+15$

$y=\underbrace{x^2+6x+\left(\frac{6}{2}\right)^2}_{=\left(x+\frac{6}{2}\right)^2}-\underbrace{\left(\frac{6}{2}\right)^2}_{=3^2=9}+15$

$y=\left(x+\frac{6}{2}\right)^2-9+15$

$y=\left(x+3\right)^2+6$

Das kann man nun mit der allgemeinen Scheitelpunktform...

$y=a\cdot \left(x-x_S\right)^2+y_S$

...vergleichen.

Bedenke, dass 1 das neutrale Element der Multiplikation ist, man vorne also quasi einen versteckten Faktor 1 hat, den man ergänzen kann. Und bedenke, dass man + 3 auch als - (-3) schreiben kann.

$y=\underbrace{1}_{a}\cdot \left(x-\underbrace{\left(-3\right)}_{x_S}\right)^2+\underbrace{6}_{y_S}$

Dementsprechend kann man im konkreten Fall den Scheitelpunkt (-3 | 6) ablesen.

Answer 4

[Halswirbelstrom]

LG H.